Свойства неприводимых многочленов.

Теорема. Все корни неприводимого многочлена имеют тот же порядок. Порядок корней неприводимого многочлена называется показателем многочлена, которому он принадлежит.

Определение. Неприводимый многочлен степени m над полем GF(q) называется примитивным, если его корень– примитивный элемент поля GF(q). (Такой, что через него можновыразить все другие элементы поля, как степени этого элемента).

Линейные переключательные схемы.

Исторически первая реализация шифрования.

Используемые типы элементов:

Полусумматор. .
Ячейка памяти, где находится переменная a. .
Умножение на коэффициент. . . .

Линейными переключательными схемами с конечным числом состояний называются любые схемы, содержащие конечное число сумматоров, устройств памяти и устройств умножения на константу, соединенных любым допустимым способом.Вход и выход предполагаются последовательными, т.е. входной сигнал состоит из элементов поля, подаваемых на вход последовательно – по одному в единицу времени.

Представление полиномов:

– фиксированный порождающий полином.

– входной полином.

Схема умножения полиномов на регистрах:

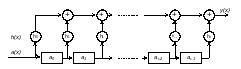
На вход схемы поступают коэффициенты . Предполагается, что сначала все регистры содержат нули, а коэффициенты полинома подаются, начиная с младшего разряда, после чего следует r нулей. Суммирование осуществляется по mod 2.

1. 1 шаг: Когда на вход ЛПС поступает старший коэффициент 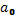, то он проходит через все сумматоры на выход при условии 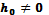, т.е. в первый момент

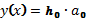
2. 2 шаг: Спустя единицу времени, с появлением на шине сдвига второго коэффициента на выходе сформируется второй коэффициент произведения полиномов:

В итоге после r шагов получим результат:

..

Схема деления полиномов с помощью регистров.

На схему поступает старшая единица. Изначально в регистрах схемы установлены все «0». Рабочий такт начнется, когда u(x) установитсяна всех регистрах схемы (r сдвигов.После этого на выходе появится первый ненулевой выход. Смысл в том, что для каждого коэффициента частого необходимо вычесть из делимого полиномG(x).

У магических полиномов всегда и .

.

Пример:

U(x) = 101011011.

.

Если приравнять к 0 или вообще убрать, то получим генератор гамма-последовательности.

Смысл соотношения: любые n тактов гамма-последовательности линейно зависимы. Если нам известны , то можно восстановить последовательность полностью.

Схема деления используется для получения CRC кода.

CRС.

Circularredundancecode.Кольцевой избыточный код, приняется для обнаружения и исправления ошибок.Раньше использовали контрольные суммы. Способ цифровой идентификации некоторой последовательности данных. Алгоритм CRC используется для контроля передаваемых данных по ненадежным линиям связи, в архиваторах.

Формальныйспособ получения CRC- деление многочлена с двоичными коэффициентами и приписанными нулями на некоторый известный фиксированный полином. Фиксированный полином P(x) можно выбрать любой, но желательно, чтобы он был неприводимым и примитивным. Распространены полином crc16 и crc32. Получать CRC коды можно используя любую схему деления полинома на полином. Можно взять пробный файл, запустить прогон с выбранным полиномом. По полученному коду оценим выбранный полином.