Алгебра классов вычетов многочленов.

Теорема:Классы вычетов многочленов по модулю многочлена образует линейное векторное пространство (линейную алгебру) размерности n над полем коэффициентов.

Классы вычетов – идеалы и смежные классы.Свойства классов вычетов полиномов:

1. Умножение на скаляр определено как умножение скаляра на все компоненты данного смежного класса: .

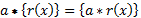Если раньше образующим элементов был r(x), то теперь произведение. Теперь это другой смежный класс.

2. Дистрибутивность и ассоциативность. Их принимают, как следствие из правил сложения и умножения многочленов и не доказывают.

3. Размерность пространства коэффициентов равна n. Т.к. это коэффициенты при степенях x, меньше чем n.

4. n классов вычетов. Т.е. {1}, {x}, {x²}, ..., {x^n-1}. Такие n классов вычетов порождают все пространство, т.е. любой из полиномов (остатков от деления) можно представить в виде линейной комбинации этих классов вычетов.

5. В классе вычетов в качестве образующего (представителя этого класса) используют многочлен минимальной степени.

Несколько теорем, иллюстрирующие эти свойства.

1. Теорема: в алгебре многочленов по модулю существует многочлен F(x) = 0, но не существует равного нулю многочлена F(x) степени меньшей, чем n.

Если образующийG(x) образует некий класс и не является идеалом, то у нас по предыдущей теореме о классах вычетов.

2. Теорема: пусть J – это идеал в алгебре многочленов по модулю F(x), а G(x) – отличный от нуля многочлен наименьшей степени такой, что класс вычетов G(x) принадлежит J. Т.е. класс вычетов S(x) принадлежит идеалу J тогда и только тогда, когда многочлен S(x) делится на G(x). Более того, многочлен G(x) является делителем F(x), если F(x) не является неприводимым.

Доказательства к теоремам являются факультативными – если мы их не поймем, то практически ничего страшного.

Доказательство:

S(x) = g(x)*q(x) + r(x), но нам известно, что g(x) *q(x) принадлежит идеалу J. =>r(x) принадлежит J.

R(x) < степени g(x) => .

Теорема: для любого идеала J в алгебре многочленов по модулю F(x) существует единственный нормированный многочлен G(x) минимальной степени такой, что класс вычетов {G(x)} принадлежит J.

Обратно: каждый нормированный многочлен G(x), являющейся делителем F(x) порождает некоторый идеал J, в котором G(x) является нормированным многочленом наименьшей степени.

Примечание: теорема следует из алгоритма деления Эвклида для полиномов. Если не нравится доказательство предыдущей теоремы, то его можно заменить этим (что она следует из Эвклида).

Классы вычетов порождают векторное пространство размерности n. А если многочлен не является неприводимым? Что же тогда? Тогда F(x) распадается на 2 сомножителя.

Если имеется делитель степени k у коэффициентов. Это аналог нуль-пространства.

Определение: нормированный многочлен G(x) минимальной степени такой, что его класс вычетов принадлежит идеалу, называется порождающим многочленом идеала.

Дальше утверждения с фразой «попытаться понять смысл следующих утверждений».

1. Каждому идеалу в алгебре многочленов по модулю F(x) соответствует порождающий многочлен G(x) порождает свой идеал.

2. Каждый класс вычетов в идеале, порожденном g(x) содержит единственный многочлен, который делится на g(x) и степень которого меньше F(x) и каждый многочлен принадлежит некоторому классу вычетов, входящему в идеал.

Определение (нужно знать, а не понимать): многочлен R(x) принадлежит нулевого пространству идеала J, если для любого S(x) принадлежащего J. Это аналог понятия перпендикуляра (перпендикулярной плоскости).

Теорема: пусть F(x), G(a) и H(x) – нормированный многочлены и пусть .

Класс вычетов принадлежит нулевому пространству тогда и только тогда, когда он принадлежит идеалу, порожденному S(x).