Вычисление длины периода последовательности (метод Флойда)

Методы вычисления длины последовательности, которые не загромождают память.

Имеется случайная функция , где –произведение двух простых чисел.

Мы не знаем, когда начался цикл.

Будем вычислять 2 последовательности:

1)

2)

Т.е. берем значения через шаг и через 2 шага. Вскоре обгонит . Пока они находятся в хвосте, это не страшно. В круге значения рано или поздно совпадут. Мы запоминаем этот момент и продолжаем вычисление. Пока 1 обежит круг 1 раз, второй – 2 раза. Посчитав, сколько шагов сделал мы получим длину периода.

Из лаб: имеется два 16-битных регистра. Поэтому используем 2 цикла: с шагом 1 и шагом 2. Во время каждой итерации производим сдвиг каждого регистра влево на количествово бит равное числу шагов и запоминаем младший бит каждого регистра. Второй цикл вскоре начнет обгонять первый цикл и в определённые момент времени значения регистров совпадут. Определив сей факт, ждём повторного совпадения значений регистров.

Метод Брента немного эффективнее, но сложнее.

Полиномы.

F(x) – это многочлен (полином) от одной переменной x с коэффициентами из некоторого поля F.

.

Определения:

1. Степень многочлена – это наибольшая степень x при слагаемом с ненулевым коэффициентом. Степень нулевого многочлена равна 0 по определению.

– многочлен степени .

2. Многочлен - нормированный, если коэффициент при наибольшей степени X = 1.

3. Многочлены можно складывать и умножать обычным путем - они образуют кольцо.

   1. Многочлены - аддитивная абеллева группа.

   2. Определено произведение многочленов.

   3. Выполняется ассоциативность

   4. Имеет место дистрибутивность

4. Если многочлены с R(x), S(x), T(x) и выполняется 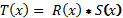, говорят, что R(x) – делитель многочлена T(x).

5. Неприводимый– многочлен P(x) степени n, который не делится ни на какой многочлен степени <n, но больше нуля.

6. НОД 2х многочленов – нормированный (иначе их могло быть много) многочлен наибольшей степени, который является делителем обоих многочленов.

7. 2 многочлена взаимнопросты, если их НОД = 1.

8. Многочлен P(x) двойственный многочлену Q(x), если его коэффициенты расположены в обратном порядке.

9. Двойственный многочлен неприводимого полинома неприводим.

Примечание: если смотреть таблицы полиномов, то там приводятся либо тот, либо другой, чтобы не удваивать объем.

10. Степень произведения двух многочленов равна сумме их степеней.

11. Ненулевой полином степени 0 – элемент поля коэффициентов.

12. Не существует многочленов больше 0, которые имели бы обратный элемент.

Многочлен степени 0 обязательно имеет обратный элемент.

13. Если S(x) делится на R(x), а R(x) делится на S(x), то они отличаются самое большее – множителем из поля коэффициентов.

Доказательство:

S(x) = q(x) *R(x),

R(x) = b(x)*S(x).

У них степени равны =>степени a(x) и b(x) = 0 – это некие множители из поля коэффициентов. Т.е. это просто коэффициенты.

14. Для любой пары многочленов существует пара многочленов Q(x) и R(x) таких, что – это алгоритм деления Евклида. Здесь можно выполнять деление столбиком. Степень полинома R(x) меньше, чем у D(x).

15. Если делитель имеет первую степень D(x) = x – a , то .

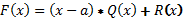А остаток имеет меньшую степень (степень меньше, чем 1).

Это свойство – теорема об остатке.

16. Если F(a)=0, т.е. a – корень многочлена F(x)=0, то R = 0 и многочлен F(a) – множитель многочлена F(x). Это теорема Безу.

Следствие к теореме Безу: т.к. степень произведения многочленов = сумме степеней сомножителей, то степень полинома F(x) по крайней мере не меньше числа корней многочлена F(x).

Следствие можно прочитать и задом наперед – количество корней полинома не больше, чем его степень.

17. НОД D(x) двух многочленов всегда можно представить в виде . Это один из вариантов теоремы Безу. Следствие из алгоритма Евклида.

Сходство колец для числовых полей с этими свойствами: соотношения для чисел «<» или «>» надо заменить на соотношения для степеней полиномов.

18. Совокупность многочленов образует идеал тогда и только тогда, когда она содержит все многочлены, кратные некоторому многочлену. Такой идеал многочленов обозначается, как J{F(x)} в фигурных скобках.

Теорема: Каждый класс вычетов по модулю многочлена содержит либо 0, либо многочлен степени, меньшей n. 0 – элемент идеала, а многочлены степеней меньше, чем n принадлежат к различным классам вычетов.

Теперь нужно распространить модульную арифметику на полиномы.