Парадокс дней рождения.

Сколько человек должно быть в комнате, чтобы с вероятностью > 50% можно было сказать, что есть два человека, родившихся в 1 день?

Возьмём наугад одного человека из группы и запомним его день рождения.Тогда ДР второго человека совпадает с ним с вероятностью , у третьего вероятность совпадения ДР с предыдущими двумя будет уже . Вычислить вероятность для n человек трудно. Проще посчитать вероятность несовпадения всех дней рождения :

–вероятность несовпадения всех ДР для человек.

.

Используя разложение экспоненциальной функции в ряд Тейлора:

.

.

Получаем .

Должно быть 22 человека, чтобы ДР не совпадали.

Альтернативный метод расчета использует комбинаторику. Но это сложно.

Факторизация.

Разложение натурального числа на простые сомножители. Сложность задачи порядка .

Метод Поларда.

Метод Флойда.

Метод Брента.

Вычисление числа по его вычетам.

Можно ли вычислить число, если известны его вычеты (остатки от деления)?

Пусть m и n – взаимно простые числа. Так, что gcd(m,n)=1.

Пусть известны вычеты y =xmodm

z = xmodn.

Нужно найти . .

Число U такое, что U*n = 1 modm–есть обратное число к одному из чисел по модулю другого числа.

.

Определение числа по его остаткам:

.

.

Пример:

n = 19687.

m = 17.

u=1.

y = 18000.

z = 13.

Найти число, которое дает остаток 18000 по модулю n и остаток 13 по модулю m.

.

.

Поиск простых чисел.

Решето Эратосфена.

Метод пробных делений.

Если n — составное, то , где , причем . Поэтому для d = 2, 3, . . ., [ ] мы проверяем, делится ли n на d? Если делитель числа n не будет найден, то n—простое. В противном случае будет найден минимальный простой делитель числа n, т.е. мы даже разложим n на два множителя.

Тест Миллера-Рабина на простоту.

Тест - модификация метода вычисления больших степеней путем повтореного возведения в квадрат.

p – вероятное простое число, нечетное.

а – свидетель простоты числа p, причем p не делится на a. Можно брать несколько случайных свидетелей.

В тесте используется:

1. малая теорема Ферма:

. Если получили 1, то это не противоречит тому, что число p – возможно простое. Если получили не 1, то p – составное число.

2. Если число n нечетное и множество целых чисел 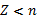содержит нетривиальный квадратный корень из 1, больший 1, то число n–составное.

Доказательство:

x²=1 modn, 1<x<n.

(x²-1)=0 modn (x-1)(x+1)=0 modn

Возможные случаи:

1. Если то и другое делит n, то (x-1)=i*n, (x+1)=j*n, то вычитаем первое из второго: 2=(j-i)*n это может быть при n=2.

2. Если n делит x-1, то (x-1)=k*nдля некоторого k.

x= 1+k*n = 1 mod n.

3. Если n делит x+1.

(x-1)=k*n

x=-1 modn = (n-1)+kn.

Если существует отличный от квадратный корень из n, то n число составное.

АлгоритмМиллера-Рабина:

bi- битовая компонента числа n (то есть 1 конкретный битовый разряд числа).

d<–1

for i=k downto 0 do

{

x<–d

d<–(d*d) mod n

if d=1 and x<>(n-1) then return TRUE

if bi=1 then d<– (d*a)mod n

if bi<>1 then return TRUE

else return FALSE

}

Если алгоритм вернет TRUE, то число составное.

Если вернет FALSE, то оно может быть составным с вероятностью не меньше 0,5.

Как проверить далее? Взять свидетелей – числа а, если свидетелей много, то при прогоне алгоритма вероятность ошибки мала.

Кармайкловы числа. Это положительные составные числа , которые удовлетворяют условию для всех целых , взаимно простых с .

Малая теорема Ферма утверждает, что любое простое число обладает выше указанным свойством. В этом смысле числа Кармайкла подобны простым. Поэтому они называются псевдопростыми числами.Кармайкловы числа имеют по меньшей мере три простых положительных множителя.

Для всех свидетелей теста в результате получаем 1. 3 первых числа Кармайкла:

561=3*11*17,

1105=5*13*17,

1729=7*13*19.

В действительности их количество стремится к нулю при увеличении разрадяности.