7 Вопрос

Основы подобия. Движение жидкости в межлопастных каналах ЦН имеет сложный характер. Поэтому при решении уравнений движения жидкости принимают ряд допущений. Исходя из сложности движения жидкости, при создании ЦН в частности и лопастных насосов вообще с лучшими эксплуатационными качествами наряду с теоретическими расчетами большое значение приобретают экспериментальные исследования и их обобщение. Обобщение результатов проводимых испытаний (например, моделей) и перенос их на другие насосы (например, натурные насосы) осуществляются на основании положения о механическом подобии потоков жидкости в них. Для этого необходимо соблюдение трех видов подобия: геометрического, кинематического, динамического. Другими словами, использование обобщенной информации испытаний модельных ЦН при проектировании (создании) натурных осуществляется с помощью теории о механическом подобии потоков жидкости. Конкретные случаи практического использования положений о механическом подобии: пересчет параметров одного насоса на параметры другого при условии геометрического подобия их проточных частей и  ; пересчет параметров насоса с одной частоты вращения на другую. При проектировании насосов широко используется моделирование. При этом модели должны быть изготовлены согласно требованиям законов подобия. Сущность геометрического подобия. В его основу положена пропорциональность сходственных линейных размеров геометрических параметров натурного и модельного насосов. Используя в качестве таких параметров соответственно для натуры и модели высоту лопасти (например, для ОН l_н, l_м) и наружный диаметр РК (например, для ЦН D_2H, D_2m), можно записать уравнение геометрического подобия

(1)

Коэффициент K₁ принято называть геометрическим масштабом или масштабом длины. Сущность кинематического подобия. Прежде всего у натурного и модельного насосов должно быть соблюдено геометрическое подобие и выдержана одинаковая ориентация модельного и натурного насосов относительно потока жидкости. Только при этих условиях можно рассматривать кинематическое подобие. В основу такого подобия положено прохождение сходственными частицами потоков жидкости (модели и натуры) подобных путей в пропорциональные отрезки времени. Используя скорости потоков жидкости для натурного и модельного насосов, можно записать уравнение кинематического подобия

(2)

Коэффициент К_C принято считать масштабом скоростей. Сущность динамического подобия. Обязательным условием такого подобия должно быть соблюдение геометрического и кинематического подобия у модельного и натурного насосов. В его основу положено постоянство отношения сил, приложенных к выделенным элементарным объемам в сходственных точках потоков жидкости. Для выполнения условия динамического подобия ЦН в частности и лопастных насосов вообще необходимо равенство двух критериев: Рейнольдса (Re) и Струхаля (Sh). В том случае, когда насос и его модель перекачивают одну и ту же жидкость, для их подобия достаточно соблюдения только условий, предусмотренных равенствами (1) и (2). Исходя из сказанного, можно записать уравнение динамического подобия при условии, что жидкость несжимаемая и вязкая, а ее движение неустановившееся:

(3)

Критерий подобия вообще характеризует отношение сил различной природы, действующих в движущейся жидкости. В частности, критерий Рейнольдса характеризует отношение сил инерции к силам вязкости, а критерий Струхаля — сил инерции, возникающих от переноса частиц, к силам, возникающим от нестационарности их движения:

(4)

где с —скорость движения частицы жидкости; l — длина прохождения ее пути;   — коэффициент кинематической вязкости;

(5)

где l —длинапути; с —скорость; Т —время. Критерий Струхаля, другими словами, характеризует подобие инерционных сил при неустановившемся движении жидкости. Условие установившегося движения жидкости  . В этом, случае  . Примеры использования теории подобия применительно к ЦН. Уравнения подобия связывают основные параметры (Q, N, H) натурного и модельного ЦН и по известным их значениям модельных насосов позволяют определить параметры натурных насосов (Q_H, N_H, H_H). Подача натурного насоса

(6)

Отношение   учитывает изменение объемных потерь, обусловленных изменением относительных значений зазоров, при существенном изменении масштаба. Мощность натурного насоса

(7)

Отношение учитывает изменение относительной величины механических потерь в подшипниках и сальниках. Напор натурного насоса

(8)

Отношение   учитывает изменение гидравлических потерь в зависимости от числа Re и геометрического масштаба. Если рассматривается один насос и к нему применяются указанные уравнения подобия, то в этом случае  . В области режимов работы насоса  объемные и гидравлические потери постоянны, поэтому и КПД равны. Исходя из этого, по известным (опытным) значениям параметров Q₁, H₁, N₁ и на одном режиме w₁ можно определить аналогичные параметры на другом режиме работыw_i по уравнениям подобия:  ;  ;  (приближенно, без учета изменения механических потерь). На подобных режимах работы насоса сохраняются постоянными отношения:  .

8 вопрос = 7 вопрос

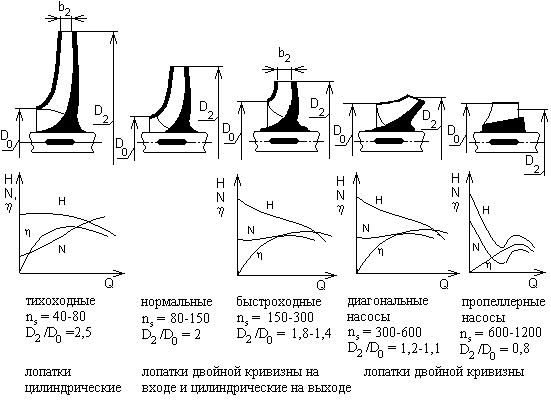
11) Коэффициент быстроходности - это частота вращения геометрически подобного насоса, имеющего такой размер, что при напоре 1 м он дает подачу 75 л/с. Служит для сравнения различных типов рабочих колес насоса, выбора насоса при заданных производительности, напоре и числе оборотов в минуту, значения которых берутся для оптимального режима, отвечающего максимальному КПД насоса.

Коэффициент быстроходности определяется по формуле:

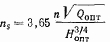
Конструкции рабочих колес

Коэффициент быстроходности рассчитывают на одно колесо и по количеству одностороннего входа в него жидкости. Наибольший КПД имеют насосы с коэффициентом быстроходности в пределах от 90 до 300. С другой стороны, насосы с n_s = 700-1200 имеют малые габариты и малый вес. Поэтому в современном насосостроении стремятся применять более быстроходные типы рабочих колес для насосов большой и малой производительности, что дает возможность уменьшить их размеры, создать насосы более компактной и легкой конструкции.

По величине коэффициента быстроходности центробежные насосы делят на:

• тихоходные, n_s = 40-80,

• нормальные, n_s = 80-150,

• быстроходные, n_s = 150-300.

На рисунке схематично изображены центробежные насосы с различными коэффициентами быстроходности и их характеристики.