16. Тест на основе экстремальной статистики дельта-произведения.

В ситуации, описанной в начале п.15, определим, вместо (15.1),статистики

Эти статистики также характеризуют «степень похожести» фрагментов , и при гипотезе они независимы в совокупности, маргинальные их распределения - биноминальные :

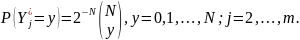
Далее строится статистика максимального дельта-произведения

которая при гипотезе имеет распределение

На основе этих результатов в [11] предложен соответствующий

1. Регистрируется последовательность длиной выбирается так, чтобы обеспечить выполнения условий применимости

2. Эта последовательность разбивается на подпоследовательностей длиной а каждая из них – на фрагментов длиной По -ой подпоследовательности, согласно (16.1), вычисляется статистик и по ним – экстремальная статистика , согласно (16.2).

3. По выборке экстремальных статистик вычисляется

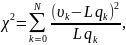
где (см(16.3))

4. Выносится решение по правилу:

Замечание. Как и в конце п.15 можно также построить и рассчитать соответствующий критерий Колмогорова.