4. Обобщенный покер тест

В этом тесте вида (1.4) - (1.7) используется частоты встречаемости некоторых комбинаций символов в n- сериях x=(x1,…,xn). Статистика T=T(x), на которой основан обобщенный покер-тест, определяется как количество различный символов в n-серии x; при этом и

где и числа - числа Стирлинга второго рода, определяемые разложением [2]

.

В частном случае n=5 имеем классический покер-тест.

5. Тест “собирателей купонов”

Этот тест обычно применяется при N>2; если исходная последовательность –двоичная, то можно увеличить мощность алфавита до значения 2­^r, рассматривая “укрупненную последовательность” фрагментов размера r>1.

В тесте “собирателя купонов” находится такой фрагмент {x1,…,xt} в исследуемой последовательности, который “впервые соберет полный комплект 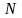купонов”, т.е. содержит все символов алфавита . Этот тест имеет вид (1.4)-(1.7) при

(5.1)

6. Тест перестановок

Это еще один из классический тестов Кнута [1], являющийся частным случаем тесте общего вида, описанного в п.1.

Для построения теста выбирается некоторое натуральное n, (для двоичной последовательности производится предварительной “укрупнение”, аналогично п.5), и рассматривается вариационный ряд

Фрагмента (x₁,…,x_n)=X.Статистика T(X) определяется следующим соотношением:

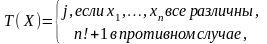(6.1)

где j=j(X)-номер перестановки, переводящий упорядоченный набор (x₍₁₎,…,x_(n)) в наблюдаемый набор (x₁,…,x_n).

При это в обозначения п.1

7. Тест пересекающихся n-грамм.

Этот тест предложен Дж. Марсальи (1985г) и использует частоты пересекающихся n-грамм в дополненной первыми n-1 символами последовательности (1.1):

Именно, рассматриваются “пересекающихся n-грамм” (со сдвигом на одну позиции.)

и для вычисляются частоты встречаемости всевозможных n-грамм:

.

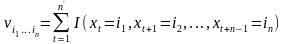Аналогично вычисляется частоты встречаемости всевозможный (n-1) - грамм { }.

Далее строится тестовая статистика

(7.1)

Доказано [3], что при распределение статистики Q при гипотезе H₀ к -распределению с числом степеней свободы :

(7.2)

На основе этого по аналогии п.1 строится решающее правило, основано на P-значении : гипотеза H₀ тогда и только тогда, когда 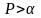, где - заданный уровень значимости.

Замечание. В качестве тестовой статистики можно также использовать статистику

, (7.3)

для которой также имеет место утверждение (7.2), и, следовательно соответствующий критерий имеет тот же вид.

8. Тест, основанный на рангах двоичных матриц.

Этот тест, входящий в «батарею статистических тестов» Дж. Марсальи, является частным случаем теста (1.4) – (1.7) и основан на вероятностных свойствах двоичной матрицы, которая строится по исследуемому фрагменту двоичной последовательности А = {0,1}.

Пусть длина n фрагмента представима в виде , где и – некоторые натуральные числа, 2 ≤ ≤ . Представим следующий фрагмент 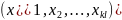в виде матрицы размером

(8.1)

и пусть статистика Т означает ранг этой матрицы:

(8.2)

Разделение статистики при нулевой гипотезе известно и имеет вид [3,4]:

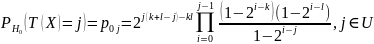(8.3)

Отметим, что случай соответствует нулевой матрице ; при этом

P₀₀=2^-kl (8.4)

Таким образом, тест, основанный на рангах двоичных матриц, имеет вид (1.4) – (1.7) с учетом обозначений (8.1) – (8.4).

В заключение отметим, что вычисление ранга (8.2) осуществляется методом Гаусса – приведением матрицы к матрице верхнего треугольного вида с помощью элементарных преобразований ее строк.