
- •Статистика
- •Статистическое тестирование дискретных случайных последовательностей.
- •1.Общий алгоритм тестирования по методу χ2.
- •2. Тест n-серий
- •3. Тест интервалов
- •4. Обобщенный покер тест
- •5. Тест “собирателей купонов”
- •6. Тест перестановок
- •7. Тест пересекающихся n-грамм.
- •8. Тест, основанный на рангах двоичных матриц.
- •9. Спектральные тесты.
- •10. Тесты случайного блуждания
- •11. Тест Маурера
- •12. Тест, основанный на алгоритме сжатия Лемпеля-Зивы.
- •13. Энтропийные тесты.
- •14. Тест, основанный на линейной сложности.
- •15. Тест на основе экстремальной статистики скалярного произведения.
- •16. Тест на основе экстремальной статистики дельта-произведения.
Статистика
Основные понятия и теоретические сведения.
1.
Статистические данные, являющиеся
исходным «материалом» в задачах
математической статистики, обычно
являются результатом наблюдения
некоторой совокупности случайных
величин
 ,
характеризующей исход изучаемого
эксперимента. В таких случаях говорят,
что эксперимент состоит в проведении
,
характеризующей исход изучаемого
эксперимента. В таких случаях говорят,
что эксперимент состоит в проведении
 испытаний, в которых результат
испытаний, в которых результат
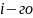 испытания описывается случайной
величиной
испытания описывается случайной
величиной
 .
В этом случае
называется выборкой
объема
,
а множество всех возможных её реализаций
.
В этом случае
называется выборкой
объема
,
а множество всех возможных её реализаций
 – выборочным пространством. Ниже будет
рассматриваться ситуации, когда элементы
выборки являются независимыми копиями
некоторой случайной величины
– выборочным пространством. Ниже будет
рассматриваться ситуации, когда элементы
выборки являются независимыми копиями
некоторой случайной величины
 с распределением
с распределением
 ,
т.е.
,
т.е.
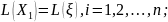 в этом случае говорят кратко, что
есть выборка
из распределения
в этом случае говорят кратко, что
есть выборка
из распределения
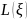 .
Статистическая модель задается классом
допустимых (возможных) распределений
наблюдаемой случайной величины
и обычно является параметрической,
т.е. когда класс допустимых функций
распределения
имеет вид
.
Статистическая модель задается классом
допустимых (возможных) распределений
наблюдаемой случайной величины
и обычно является параметрической,
т.е. когда класс допустимых функций
распределения
имеет вид
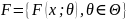 ,
где
,
где
 -
неизвестный параметр распределения;
множество
-
неизвестный параметр распределения;
множество
 возможных значений
называется параметрическим
множеством
модели. Для таких моделей распределение
вероятностей на выборочном пространстве
возможных значений
называется параметрическим
множеством
модели. Для таких моделей распределение
вероятностей на выборочном пространстве
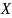 ,
отвечающее параметру
,
обозначается символом
,
отвечающее параметру
,
обозначается символом
 .
.
2.
Всякая случайная величина
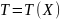 ,
являющаяся функцией ишь от выборки
,
называется статистикой,
а любая теоретическая характеристика
наблюдаемой случайной величины
является некоторой функцией от параметра
.
В статистических задачах речь идет либо
об оценивании по наблюдениям
той или иной параметрической
функции
,
являющаяся функцией ишь от выборки
,
называется статистикой,
а любая теоретическая характеристика
наблюдаемой случайной величины
является некоторой функцией от параметра
.
В статистических задачах речь идет либо
об оценивании по наблюдениям
той или иной параметрической
функции
 ,
либо о проверке тех или иных статистических
гипотез о параметре
(или функции от него ).
,
либо о проверке тех или иных статистических
гипотез о параметре
(или функции от него ).
Если
для оценивания параметрической функции
используется некоторая статистика
 ,
то
называется оценкой
(для
).
Обычно в качестве меры точности оценки
используют среднеквадратическую
ошибку
,
то
называется оценкой
(для
).
Обычно в качестве меры точности оценки
используют среднеквадратическую
ошибку
 ,
и среди всех возможных оценок ищут
такую, для которой среднеквадратическая
ошибка минимальна. Часто ограничиваются
лишь несмещенными
оценками,
т.е. такими, для которых выполняется
условие несмещенности :
,
и среди всех возможных оценок ищут
такую, для которой среднеквадратическая
ошибка минимальна. Часто ограничиваются
лишь несмещенными
оценками,
т.е. такими, для которых выполняется
условие несмещенности :

функция , для которой это уравнение имеет решение, называется оцениваемой.
Для
несмещенных оценок
 ,
т.е. мерой точности таких оценок является
дисперсия, а оптимальной
оценкой
является оценка с минимальной дисперсией,
для нее используется обозначение
,
т.е. мерой точности таких оценок является
дисперсия, а оптимальной
оценкой
является оценка с минимальной дисперсией,
для нее используется обозначение
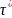 .
Оптимальная оценка (в заданной модели
.
Оптимальная оценка (в заданной модели
 и для заданной функции
)
существует не всегда, но в тех случаях,
когда она существует, она единственна.
и для заданной функции
)
существует не всегда, но в тех случаях,
когда она существует, она единственна.
Обязательным для любого правила оценивания является свойство состоятельности, означающее сходимость по вероятности оценки к оцениваемой характеристике при неограниченном возрастании объема выборки .
3.
Пусть
 -плотность
распределения наблюдаемой случайной
величины
(или вероятность события
-плотность
распределения наблюдаемой случайной
величины
(или вероятность события
 –
в дискретном случае) и
–
в дискретном случае) и
 – функция
правдоподобия данных
(выборки
).
Если
– функция
правдоподобия данных
(выборки
).
Если
 при всех
при всех
 ,
функция
,
функция
 дважды дифференцируема по
,
существует второй момент
дважды дифференцируема по
,
существует второй момент

называется функцией информации (или информацией Фишера), то модель называется регулярной (большинство рассматриваемых ниже являются таковыми).
Для регулярной модели любая несмещенная оценка дифференцируемой функции удовлетворяет неравенству Рао-Крамера:

Оценка
 ,
для которой эта нижняя граница достигается
называется эффективной
(она и является оптимальной). В заданной
модели
эффективная оценка может существовать
только для какой-то одной параметрической
функции
.
,
для которой эта нижняя граница достигается
называется эффективной
(она и является оптимальной). В заданной
модели
эффективная оценка может существовать
только для какой-то одной параметрической
функции
.
Если
модель
обладает полной
достаточной
статистикой т.е. существует статистика
такая, что функция правдоподобия
 может быть представлена в виде
может быть представлена в виде

где
функция
 не зависит от
(критерий
факторизации),
и при этом уравнение
не зависит от
(критерий
факторизации),
и при этом уравнение
 имеет
лишь решение
имеет
лишь решение
 (на множестве значений статистики
(на множестве значений статистики
 ),
то оптимальная не смещенная оценка
),
то оптимальная не смещенная оценка
 для функции
удовлетворяет уравнению
не смещенности
для функции
удовлетворяет уравнению
не смещенности

Это
уравнение либо имеет единственное
решение, либо решений нет. В последнем
случае функция
 не является оцениваемой. Таким образом,
для полной достаточной статистики
всякая функция от нее является оптимальной
оценкой своего среднего.
не является оцениваемой. Таким образом,
для полной достаточной статистики
всякая функция от нее является оптимальной
оценкой своего среднего.
4.
Одним из наиболее универсальным методом
оценивания неизвестных параметров
распределений является метод
максимального правдоподобия.
По этому методу оценкой
максимального правдоподобия
(о.м.п.)
 по выборке
,
является такая точка параметрического
множества
,
в которой функция правдоподобия
по выборке
,
является такая точка параметрического
множества
,
в которой функция правдоподобия
 достигает максимума т.е.
достигает максимума т.е.

Для
произвольной параметрической функции
ее о.м.п. находится по правилу
 .
.
Для
регулярных моделей оценки максимального
правдоподобия обладает свойствами
состоятельности, асимптотической
нормальности и асимптотической
эффективности : если
– непрерывно дифференцируемая функция,
то при


5.
При доверительном оценивании функции
ищут две такие статистики
 для которых при заданном доверительном
интервале
для которых при заданном доверительном
интервале
 выполняется условие
выполняется условие
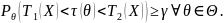
Такой
случайный интервал
 называется
называется
 доверительным
интервалом
для
.
доверительным
интервалом
для
.
Для больших выборок (при ) в ряде случаев удается построить приближенные доверительные интервалы, основанные на оценках максимального правдоподобия. Так если – непрерывно дифференцируемая функция, то в случае регулярной модели асимптотический доверительный интервал для имеет вид
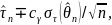
где
 и
и
 (
( – стандартная нормальная функция
распределения). В частности, для самого
параметра
такой интервал есть
– стандартная нормальная функция
распределения). В частности, для самого
параметра
такой интервал есть
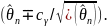
6.
В случае параметрической модели
статистические гипотезы формируются
в терминах параметра
,
и в общем случае основная гипотеза
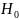 имеет вид утверждения
имеет вид утверждения
 при некотором подмножестве
при некотором подмножестве
 ,
а альтернатива
,
а альтернатива
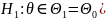 .
При заданном уровне значимости
.
При заданном уровне значимости
 (вероятности отвергнуть гипотезу
,
когда она верна) критерий проверки
гипотезы
задаётся выбором такого критического
множества
(вероятности отвергнуть гипотезу
,
когда она верна) критерий проверки
гипотезы
задаётся выбором такого критического
множества
 в выборочном пространстве
,
для которого выполняется условие
в выборочном пространстве
,
для которого выполняется условие

В
этом случае критерий (называется
критерием
 )
формулируется следующим образом : если
)
формулируется следующим образом : если
 – наблюдавшаяся
– наблюдавшаяся
реализация
выборки
X,
то при
 X1α
гипотезу H0
отвергают (принимают альтернативную
H1),
если же
X0α
=1α,
то гипотезу H0
принимают.
X1α
гипотезу H0
отвергают (принимают альтернативную
H1),
если же
X0α
=1α,
то гипотезу H0
принимают.
О качестве критерия X1α судят по его функции мощности
W(X1α;
θ)
= Pθ(X X1α),
θ
ϴ:
X1α),
θ
ϴ:
вероятность ошибки первого рода равна W(X1α; θ), θ ϴ0, а вероятность ошибки второго рода есть 1-W(X1α; θ), θ ϴ1.
Критерий
X называется равномерно
наиболее мощным
(р.н.м.), если для любого другого критерия
X1α
выполняются условия:
называется равномерно
наиболее мощным
(р.н.м.), если для любого другого критерия
X1α
выполняются условия:
W(X
;
θ)
 W(X1α;
θ)
при θ
ϴ0,
W(X1α;
θ)
при θ
ϴ0,
W(X ; θ) W(X1α; θ) при θ ϴ1.
Часто
ограничиваются рассмотрением только
несмещенных
критериев, для которых выполняется
дополнительное условие W(X1α;
θ)
α
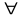 θ
ϴ1.
θ
ϴ1.
В
теории удобно рассматривать так
называемые рандомизированные критерии,
когда при наблюдении x
гипотезу H0
отвергают с некоторой вероятностью
 и принимают с дополнительной вероятностью
1-
.
Такая функция
,
X,
называется критической;
в этом случае функция мощности определяется
так: W(
и принимают с дополнительной вероятностью
1-
.
Такая функция
,
X,
называется критической;
в этом случае функция мощности определяется
так: W( ,
θ) = Eθ
,
θ) = Eθ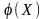 .
.
7. В основе большинства способов построения оптимальных критериев лежит фундаментальный результат (Ю. Нейман и Э. Пирсон) о существовании наиболее мощного критерия в задаче проверки простой гипотезы при простой же альтернативе.
Именно, если ϴ = {θ0, θ1}, то при любом уровне значимости α наиболее мощный критерий для гипотезы H0: θ = θ0 при альтернативе H1: θ = θ1 существует и задается критической областью
X
=
 (*)
(*)
Если
проверяется простая гипотеза H0:
θ
= θ0
против сложной альтернативы H1:
θ
ϴ\{
θ0},
то р.н.м. критерий существует, если
критическая область X
= X
(θ0,
θ1),
определенная соотношением (*), не зависит
от θ1
ϴ\{
θ0}:
в этом случае X
и есть р.н.м. критерий. Такое обстоятельство
имеет место для важного класса моделей
F = {F(x;θ),
θ
ϴ},
обладающих монотонным
отношением правдоподобия
(т.е. таких, которые обладают достаточной
статистикой T(X),
и при этом функция
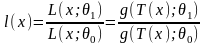 (см. выше критерий факторизации) монотонна
по T),
и в случае односторонних альтернатив
(см. выше критерий факторизации) монотонна
по T),
и в случае односторонних альтернатив
 или
или
 (здесь θ
– скалярный параметр).
(здесь θ
– скалярный параметр).
Более
того, для таких моделей р.н.м. критерий
в задаче ( ,
)
является одновременно р.н.м. критерий
и в задаче (
,
)
является одновременно р.н.м. критерий
и в задаче ( ,
)
при том же уровне значимости (аналогичное
утверждение справедливо и для двойственной
проблемы проверки
,
)
при том же уровне значимости (аналогичное
утверждение справедливо и для двойственной
проблемы проверки
 против
).
против
).
В частности, для экспоненциальной модели, задаваемой плотностью

статистика
 достаточна, и если функция A(θ)
строго монотонна, то вид р.н.м. критериев
X
указан в следующей таблице
достаточна, и если функция A(θ)
строго монотонна, то вид р.н.м. критериев
X
указан в следующей таблице
|
|
|
A(θ) ↑ |
|
|
A(θ) ↓ |
|
|
При
проверке простой гипотезы
против двусторонней альтернативы
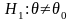 используется прием объединения двух
односторонних критических областей
соответственно для гипотез
и
,
т.е. используют критерий вида
используется прием объединения двух
односторонних критических областей
соответственно для гипотез
и
,
т.е. используют критерий вида
X1α
= X X
X при α1
+ α2
= α.
при α1
+ α2
= α.
Особый интерес представляют малые отклонения от нулевой гипотезы . В этом случае при исследовании свойств критерия ограничиваются анализом локального поведения функции мощности W(θ) в окрестности точки θ0 и строят локальный наиболее мощный критерий.
8.
Одним из наиболее удивительных методов
построения критериев проверки сложных
параметрических гипотез является метод
отношения правдоподобия.
Общий вид критерия
отношения правдоподобия
(к.о.п.) для проверки гипотезы
 таков:
таков:
X1α
= X1α
 ,
,
где граница cα выбирается из условия
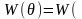 X1α
X1α .
.
Во
многих случаях такой подход приводит
к удовлетворительным решениям. Кроме
того, при некоторых условиях к.о.п.
обладает свойством асимптотической
оптимальности для больших выборок
 .
.




