Если в пространстве ввести систему координат, то точка р в этой
системе
будет иметь определенные координаты
и скалярная величина
станет функцией этих координат:
.
Обратно, всякая функция трех переменных
задает некоторое скалярное поле.
Скалярное поле часто геометрически
изображается с помощью так называемых
поверхностей уровня.
Определение. Поверхностью уровня скалярного поля называется геометрическое место точек пространства, в которой функция поля имеет одно и тоже значение С.
Уравнение
поверхности уровня имеет вид :
,
придавая С различные значения, получим
семейство поверхностей уровня.
Например,
если поле задано функцией
,
то поверхностями уровня будут сферы
с центром в начале координат.
Наряду
со скалярным полем в пространстве
рассматриваются также плоские скалярные
поля. Функция плоского скалярного поля
зависит то двух переменных:
Плоские скалярные поля изображаются геометрически с помощью линий уровня. Для функции плоского скалярного поля линия уровня имеет следующий вид: , где с – постоянная.
Например,
для плоского скалярного поля, заданного
функцией
,
линиями уровня являются равносторонние
гиперболы.
.
Пусть задана дифференцируемая функция скалярного поля .
Рассмотрим
точку
этого поля и луч
,
выходящий
из точки Р в направлении единичного
вектора
,
где
углы вектора
с осями координат.
Пусть
- какая-нибудь другая точка этого луча.
Обозначим через
расстояние между точками
и
.
Определение. Производной функции по направлению
называется
предел
и обозначается символом
.
Заметим, что если производная функции в точке по данному направлению положительна, то функция в этом направлении возрастает, если же <0, то функция в этом направлении убывает.
Можно
сказать, что производная по направлению
дает скорость изменения функции
в этом направлении. Выведем формулу
для вычисления производной по направлению.
Прежде всего заметим, что
.
Так
как функция
по условию дифференцируема, то
+
+
+
,
а тогда
+
+
+
.
Следовательно,
+
+
,
так как
=
=0,
то
+
+
.
В
случае плоского скалярного поля
производная по направлению имеет
следующий вид:
+
.
Пример.
1)Найти
производную функции
в точке
по
направлению, идущему от точки
к точке
.
Находим
вектор
и соответствующий ему единичный вектор
.
Таким образом
,
,
.
Теперь найдем частные производные
,
и их значения в точке
:
.
Тогда
.
2)
Найти производную функции
в точке ( 1, 1 ) в направлении биссектрисы
первого координатного угла.
Единичный
направляющий вектор
биссектрисы первого координатного
угла равен
.
.
Тогда
.
Градиент скалярного поля.
Определение. Градиентом в точке скалярного поля, заданного дифференцируемой функцией , называется вектор, равный
=
+
+
.
Пример.
1)
Найти
градиент функции
в точке
.
Найдем
,
,
.
+
+
=
.
2)
Найти градиент функции
,в
точке
.
,
.
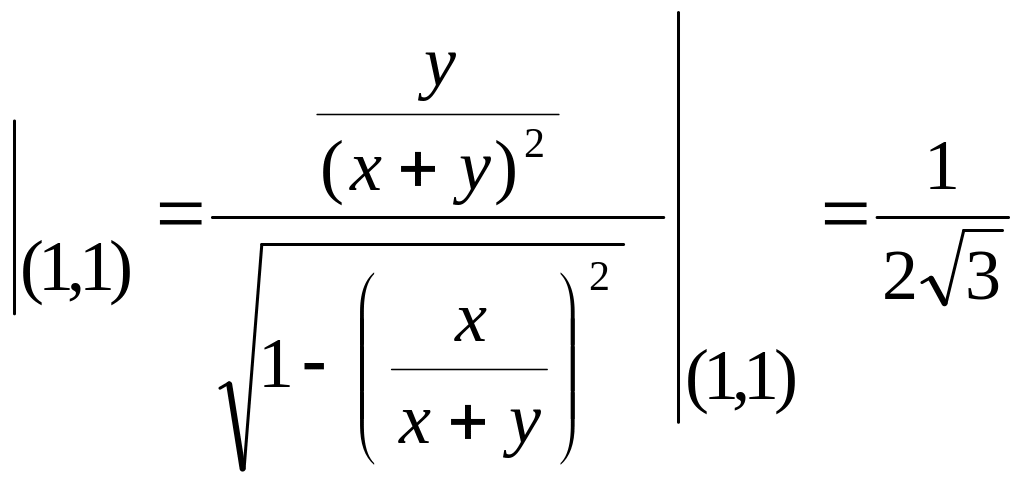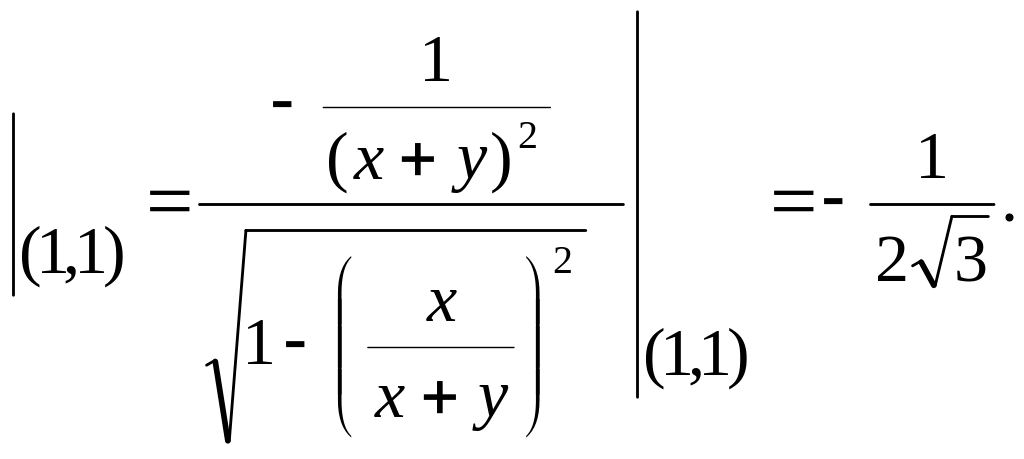
Теорема.
Проекция
вектора
на единичный вектор
равна производной по направлению
:
.
Пусть . Известно, что проекция какого-либо вектора на единичный вектор равна скалярному произведению этих векторов.
Поэтому
+
+
=
.
Обозначим
через
угол между единичным вектором
и
.
Тогда
=
.
Если
направления векторов
и
совпадают,
то производная по направлению
,
имеет наибольшее значение, равное
.
Таким образом, мы приходим к выводу: градиент есть вектор, указывающий направление наибольшего возрастания поля в данной точке и имеющей
модуль, равный скорости этого возрастания.
Пример.
Найти
наибольшую скорость возрастания функции
в
точке
:
.
В
точке
.
Следовательно, наибольшая скорость
возрастания функции равна
.
Выясним
взаимное расположение
=
в данной точке
и поверхности уровня, проходящей через
эту точку.
Пусть
уравнение этой поверхности имеет вид
.
Рассмотрим
кривую
,
лежащую на этой поверхности и проходящую
через точку
.
Предположим, что эта кривая задана уравнениями
,
где
дифференцируемые функции, причем
.
Каждая
точка кривой
имеет координаты
,
которые должны удовлетворять уравнению
поверхности уровня, поскольку кривая
полностью лежит на этой поверхности.
Таким образом,
.
Дифференцируя обе части этого тождества по , получим
.
В частности при
имеем
.
Левая
часть этого равенства является скалярным
произведением
и вектора
,
направленного по касательной к кривой
.
Таким образом,
.
Предположим,
что
.
Тогда из последнего равенства вытекает,
что
перпендикулярен вектору
.
Так как кривая была выбрана произвольно,
то мы приходим к следующему выводу.
Все
касательные, проведенные в точке
к линиям, лежащим на поверхности уровня
и проходящим через точку
,
расположены в одной плоскости,
перпендикулярной вектору
,
при условии, что этот вектор не равен
нулю.
Касательная плоскость и нормаль к поверхности
Пусть
поверхность задана уравнением
,
левая часть которого является функцией
дифференцируемой в некоторой области.
Эта функция
определяет скалярное поле,
является одной из поверхностей уровня.
Пусть в точке , тогда все касательные, проведенные в точке к линиям, лежащим на поверхности уровня и проходящим через точку , расположены в одной плоскости, перпендикулярной вектору .
Эта плоскость называется касательной плоскостью к поверхности , точке .
Найдем уравнение этой плоскости. Оно будет иметь вид:
Так
как вектор
=
+
+
перпендикулярен касательной плоскости,
то его можно принять за нормальный
вектор этой плоскости, т.е. можно положить
,
,
.
Тогда уравнение плоскости, проходящей через заданную точку с заданным вектором нормали, будет уравнением касательной плоскости, т.е.
.
Пусть поверхность имеет в некоторой точке касательную плоскость. Определение. Прямая, проходящая через эту точку перпендикулярно этой плоскости, называется нормалью к поверхности в точке .
Вектор
,
очевидно, направлен вдоль нормали и
поэтому может быть принят в качестве
ее направляющего вектора. Тогда
каноническое уравнение нормали имеет
следующий вид:
.
Пример.
1)Найти
уравнения касательной плоскости и
нормали к однополостному гиперболоиду
в точке
.
.
Найдем частные производные:
, , , тогда
+ + = .
Искомые уравнения плоскости и нормали будут следующими:
,
.
2) Найти уравнения касательной плоскости и нормали к поверхности
в
точке ( 1,1,1 ).
.
Найдем частные производные:
,
,
,
тогда
+
+
=
.
Искомые уравнения плоскости и нормали будут следующими:
,
.