МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ

Утверждена на заседании кафедры ИСС 26 апреля 2011 г.

Методические указания

по курсу

Высшая математика

Дифференциальное исчисление функций многих переменных

для бакалавров дневной формы обучения

Ростов-на-Дону

2011

УДК 512.8 (08)

Методические указания по курсу высшая математика «Дифференциальное исчисление функций нескольких переменных» для бакалавров дневной формы обучения. – Ростов н/Д: Рост. гос. строит. ун-т, 2011. – 24 c.

Изложен теоретический материал по дифференциальному исчислению функций нескольких переменных.

Предназначена для бакалавров дневной формы обучения специальностей института ПГС.

Электронная версия находится в библиотеке, ауд. 224.

УДК 512.8 (08)

Составители:

канд. физ.-мат. наук, доц. А.Е.Богданов

асс. Н.А. Кучма

Рецензент:

д-р физ.-мат. наук, проф. А.А. Ляпин

Редактор Т.М. Климчук

Доп. план 2011 г., поз. 16

Подписано в печать 18.07.11. Формат 60х84/16.

Бумага белая. Ризограф. Уч.-изд. л. 1,0. Тираж 100 экз. Заказ 223

Редакционно-издательский центр

Ростовского государственного строительного университета

344022, Ростов н/Д, ул. Социалистическая, 162

 РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ

СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ, 2011

Дифференциальное исчисление функций нескольких переменных

Функция одной переменной определяет фактически две переменные величины – аргумент и функцию . При этом переменная является зависимой и определяется по заданному закону значением независимой переменной .

В реальных процессах часто наблюдается наличие двух и более независимых переменных. Например, рельеф поверхности земли можно описать в Декартовой системе координат как функцию двух независимых переменных , где значения переменных и не зависят друг от друга.

Определение. Переменная (область изменения ) называется функцией независимых переменных , если каждой паре по некоторому правилу или закону ставится в соответствие одно определенное значение .

Аналогичным образом можно ввести понятие функции многих независимых переменных.

Частные производные первого порядка

Рассмотрим функцию двух переменных .Зафиксируем один из аргументов, например, , положив = .Тогда функция будет функцией одной переменной .Пусть она имеет производную в точке :

.

Эта производная называется частной производной первого порядка функции по в точке Р . - называется частным приращением по функции в точке Р( .Тогда можно записать , если этот предел существует. Аналогично определяются и обозначаются частное приращение функции по в точке Р( .

.

Частные производные, рассматриваемые как функции двух переменных, обозначаются следующим образом:

или или .

Примеры.

Найти частные производные функций:

1.

Частную производную находим как производную функции по аргументу в предположении, что . Поэтому .

Аналогично .

2.

3.

4.

, , .

Частные производные высших порядков

Частные производные функции нескольких переменных являются функциями тех же переменных. Эти функции в свою очередь могут иметь частные производные, которые будем называть частными производными второго порядка исходной функции. Функция имеет четыре частных производных второго порядка, которые определяются и обозначаются следующим образом:

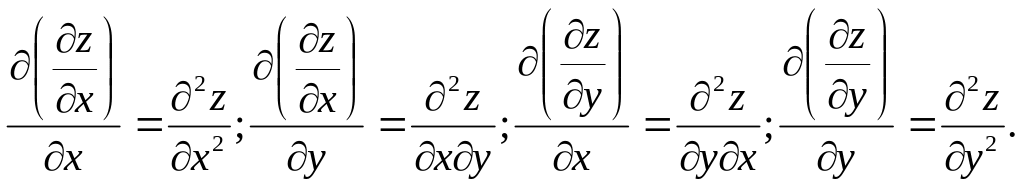
Функция имеет девять частных производных второго порядка:

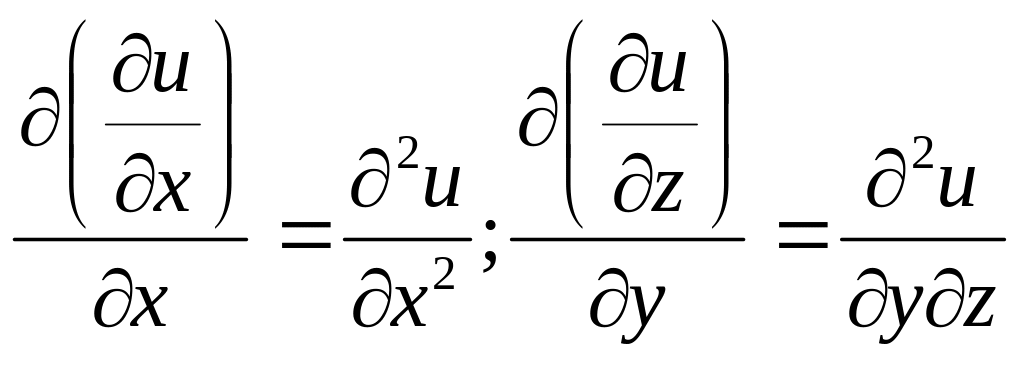и т.д.

Аналогично определяются и обозначаются частные производные третьего и более высокого порядка функции нескольких переменных. Частной производной n-го порядка функции нескольких переменных называется частная производная первого порядка от частной производной (n-1)-го порядка той же функции.

Например, частная производная третьего порядка функции ,

.

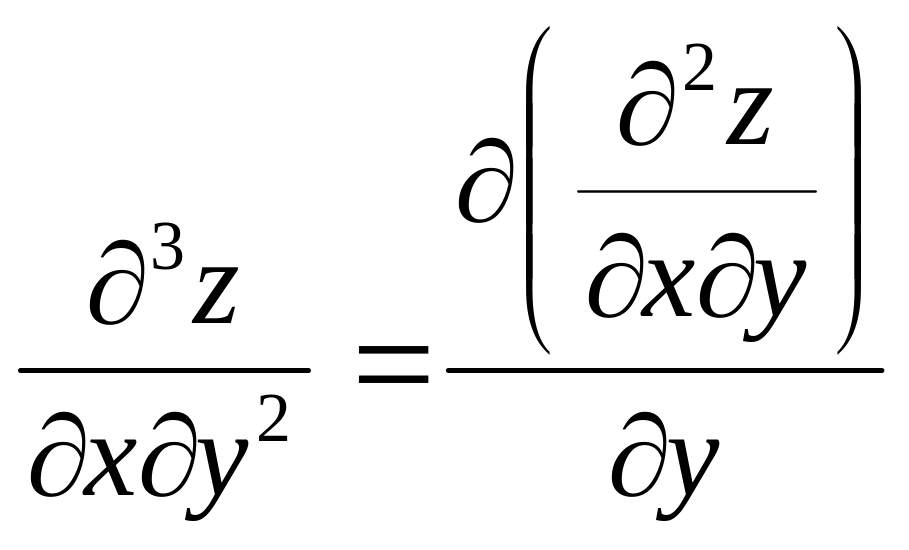Частная производная второго или более высокого порядка, взятая по нескольким различным переменным, называется смешанной частной производной. Относительно частных производных имеет место следующая теорема.

Теорема: Две смешанные частные производные одной и той же функции, отличающиеся лишь порядком дифференцирования, равны между собой при условии их непрерывности. В частности, для функции двух переменных имеем:

Примеры.

1. Найти , , от функции .

,

, , .

2) Найти от функции .

, ,

.

Полный дифференциал функции нескольких переменных

Пусть дана функция двух переменных . Предположим, что ее аргументы получают соответственно приращения и . Тогда функция получает полное приращение , которое определяется следующей формулой:

Определение. Функция называется дифференцируемой в точке P , если ее полное приращение можно представить в следующем виде: где и - любые приращения соответствующих аргументов и в окрестности точки Р; А и В – постоянные; - бесконечно малая более высокого порядка, чем расстояние между точками ( и .

Определение. Главная часть приращения функции , линей относительно и , называется полным дифференциалом этой функции и обозначается символом или .

В выражении для дифференциала величины А и В не зависят от и , но являются функциями от и . Вид этих функций устанавливается следующей теоремой.

Теорема. Если функция в точке дифференцируема, то она имеет в точке первые частные производные и , причем

Т.е. .

Как и в случае функции одной переменной, введем обозначения: . Тогда выражение для дифференциала примет следующий вид:

Теорема. Если частные производные и функции непрерывны в окрестности точки , то эта функция в точке дифференцируема.

Пример.

Найти полный дифференциал функции в произвольной точке:

.

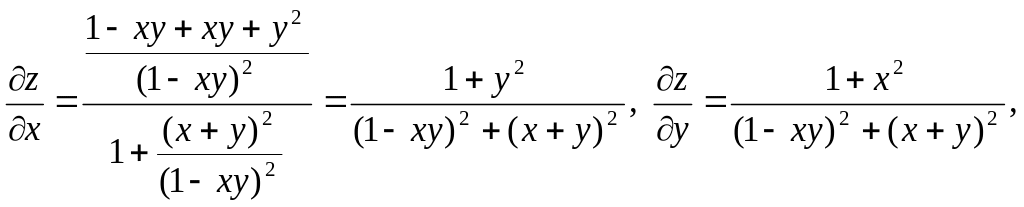
Пусть дана дифференцируемая функция . Ее полное приращение выражается формулой:

При малых и , слагаемым можно пренебречь и писать: . (1)

Так как , то Подставляя это выражение для в формулу (1), получим , откуда

. (2)

Формулой (2) можно пользоваться для приближенных вычислений значений функции двух переменных в точке близкой к точке , если известны значения функции и ее частных производных в самой точке .

Приложение полного дифференциала к приближенным вычислениям