Тест 3 Многочлени над різними полями
Кожен многочлен, степінь якого більша за 1 є … у полі :
а) незвідним;
б) звідним;
в) зведеним;
г) примітивним.
Скільки коренів має многочлен -го степеня над полем :
а) рівно
;
б) рівно ;
в) рівно
;
г) не менше .
Який вигляд має дискримінант кубічного рівняння
:
а)
;
б)
;
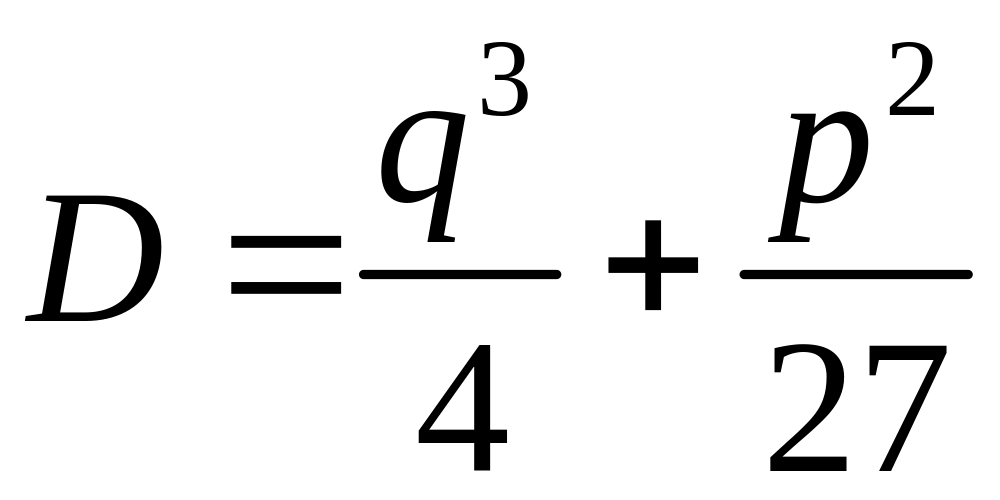в)
;
г)
.
При якій умові кубічне рівняння має один дійсний корінь і два комплексних спряжених кореня:
а)
;
б)
;
в)
;
г)
.
При якій умові кубічне рівняння має три дійсних корені (два з яких рівні):
а) ;
б) ;
в) ;
г) .
При якій умові кубічне рівняння має три різних дійсних кореня:
а) ;
б) ;
в) ;
г) .
Довільний многочлен ненульового степеня з комплексними коефіцієнтами має хоча б один … корінь (основна теорема теорії многочленів):
а) цілий;
б) раціональний;
в) дійсний;
г) комплексний.
Якщо комплексне число
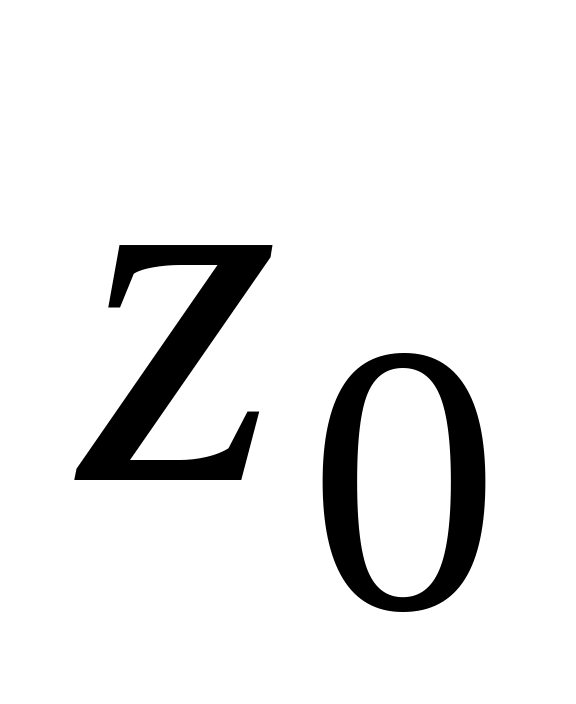- є коренем многочлена
з дійсними коефіцієнтами, то спряжене
комплексне
число
…
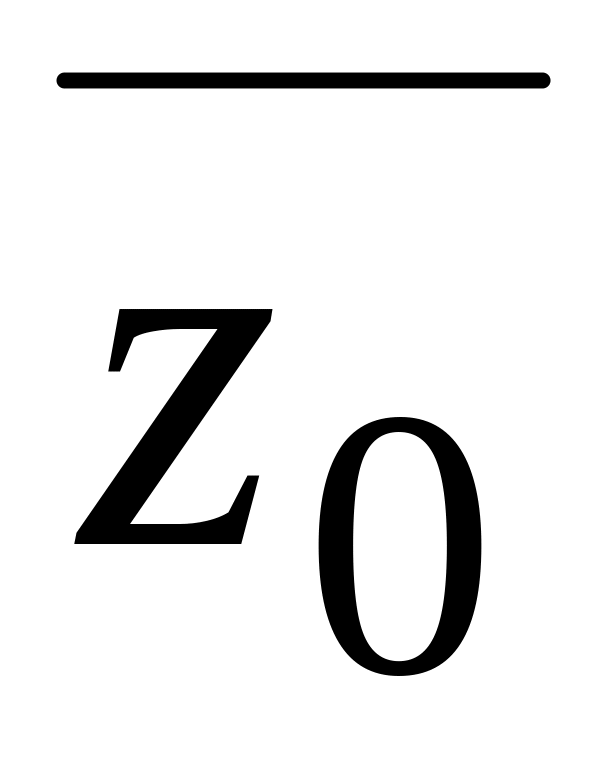а) не є коренем цього многочлена;
б) є коренем цього ж многочлена;
в) є коренем многочлена з протилежними знаками;
г) є коренем многочлена з коефіцієнтами, оберненими до даних.
Якщо комплексне число - є коренем -ї кратності многочлена з дійсними коефіцієнтами, то спряжене комплексне число є коренем …
а)
-ї
кратності;
б)
-ї
кратності;
в) -ї кратності;
г) нульової кратності.
Всі дійсні корені рівняння
містяться в інтервалі
,
де
і ...
а)
;
б)
;
в)
;
г)
.
Щоб відокремити дійсні корені многочлена необхідно знайти інтервали, у яких …
а) не лежить жодного кореня;
б) лежить один корінь;
в) лежать два кореня;
г) лежать всі корені.
Якщо , зростаючи, проходить через корінь якої-небудь проміжної функції ряду, але не проходить через корінь , то число змін знаків у ряді Штурма при цьому …
а) не зміниться;
б) зросте на 1;
в) зменшиться на 1.
Якщо і
(
)
– довільні дійсні числа, які не є
коренями
,
то число
дійсних коренів многочлена
в інтервалі (
)
дорівнює
…,
де
і
є число змін знаків у ряді Штурма
відповідно у точках
і
:
а)
;
б)
;
в)
;
г)
.
Яким є поле розкладу многочлена
:
а) Z;
б) Q;
в) R;
г) C.
Яким є поле розкладу многочлена
:
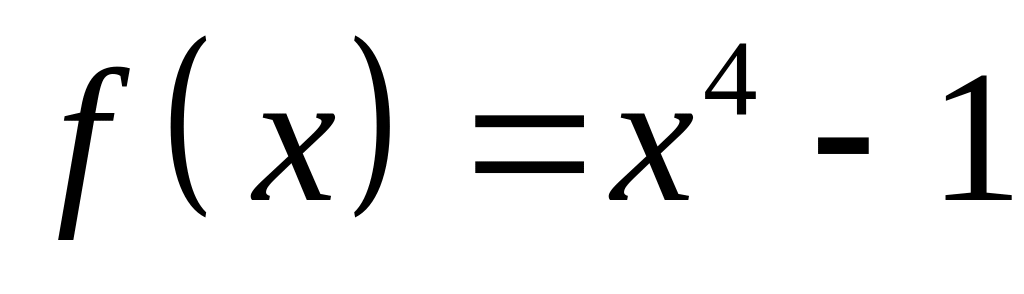а) Z;
б) Q;
в) R;
г) C.
Яким є поле розкладу многочлена
:
а) Z;
б) Q;
в) R;
г) C.
Коренем многочлена
є …
а) ;
б) 3;
в) ;
г)
.
Чи є звідним над полем С многочлен
:
а) так;
б) ні;
в) при певному ;
г) можливо.
Яке максимальне число змін знаків може мати многочлен -го степеня:
а) ;
б) ;
в) ;
г)
.
Щоб дріб , де (
)
= 1 було коренем рівняння з цілими
коефіцієнтами необхідно, щоб
…
многочлена
,
а
- …
а) було дільником вільного члена, а було б дільником старшого коефіцієнта;
б) було дільником старшого коефіцієнта, а було б дільником вільного члена;
в) було дільником вільного члена, а не було б дільником старшого коефіцієнта;
г) не було б дільником вільного члена, а було б дільником старшого коефіцієнта.
Щоб дріб , де ( ) = 1 був раціональним коренем многочлена з цілими коефіцієнтами , необхідно, щоб при довільному цілому число
ділилося на …
а)
,
де
0;
б)
,
де
0;
в) , де 0;
г) , де 0.
Якщо в многочлені з цілими коефіцієнтами
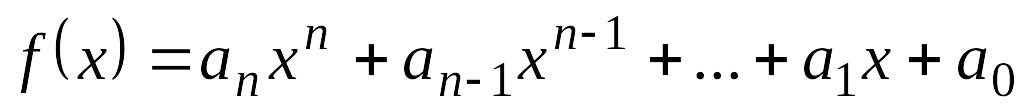коефіцієнти
діляться на деяке просте число
,
причому
…,
а старший коефіцієнт
…,
то многочлен
незвідний
у полі раціональних чисел:
а) не ділиться на , і не ділиться на ;
б)
не ділиться на
,
і
не ділиться на
;
в)
не ділиться на
,
і
не ділиться на
;
г) не ділиться на , і не ділиться на .
Многочлени і з кільця є взаємно простими. Чи можуть вони мати спільний комплексний корінь
:
а) так;
б) ні;
в) при певному ;
г) при певному .
Чи може незвідний у кільці многочлен мати кратні комплексні корені :
а) так;
б) ні;
в) при певному ;
г) при певному .
Нехай є многочлен
.
Яка заміна приводить до многочлена
виду
:
а)
;
б)
;
в)
;
г)
.
Якщо , зростаючи, проходить через корінь многочлена , то число змін знаків у ряді Штурма …
а) не зміниться;
б) зменшиться на 1;
в) збільшиться на 1.
Задача 1: знайти многочлен найменшого степеня, в якого число є трикратним коренем, -5 – двократним, а 3 є простим коренем:
а)
;
б)
;
в)
;
г)
.
Задача 2: знайти суму квадратів коренів многочлена
:
а)
;
б)
;
в)
.
Задача 3: розв’язати рівняння
:
а)
;
б)
;
в)
.
Задача 4: відокремити дійсні корені многочлена
:
а) один
комплексний корінь в інтервалі
;
б) два дійсних кореня в інтервалі ;
в) один дійсний корінь в інтервалі .
Задача 5: знайти всі раціональні корені многочлена
:
а)
;
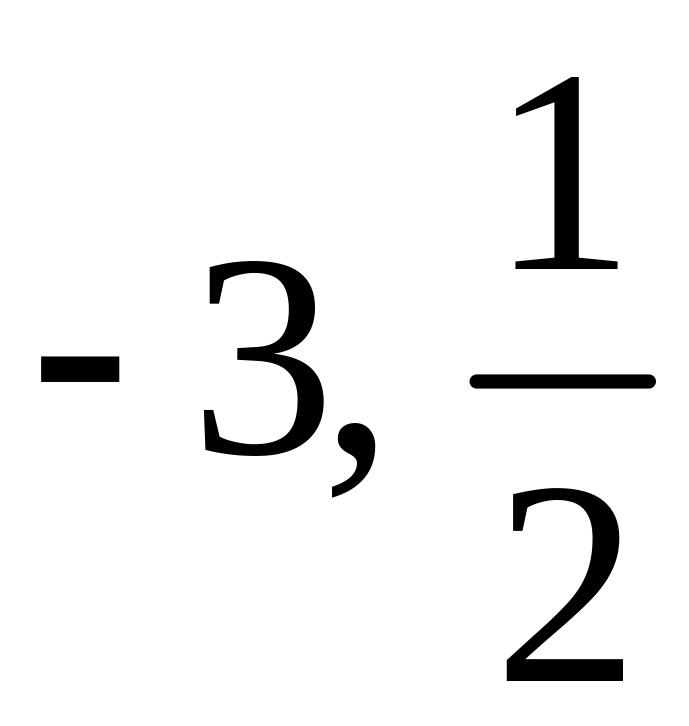б)
;
в) раціональних коренів немає.