§ 14. Позбавлення від алгебраїчної ірраціональності в знаменнику дробу Питання для самоконтролю:

1) На яких фактах ґрунтуються основні методи розв’язування задач на позбавлення від ірраціональності в знаменнику дробу?

2) Що треба зробити, щоб позбавиться від ірраціональності в знаменнику дробу ?

Задачі

1) Позбавитися від ірраціональності в знаменнику дробу:

де , де

2. Позбавитися від ірраціональності в знаменнику дробу:

3. Позбавитися від ірраціональності в знаменнику дробу:

4. Позбавитися від ірраціональності в знаменнику дробу:

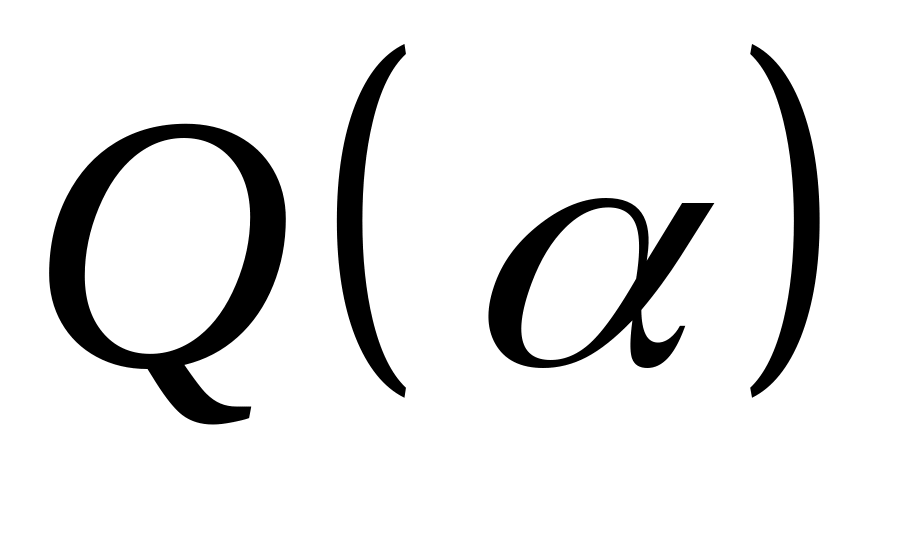5. В полі , де , знайти представлення для числа у вигляді .

6. Звільнитись від в знаменнику дробу , якщо - корінь рівняння .

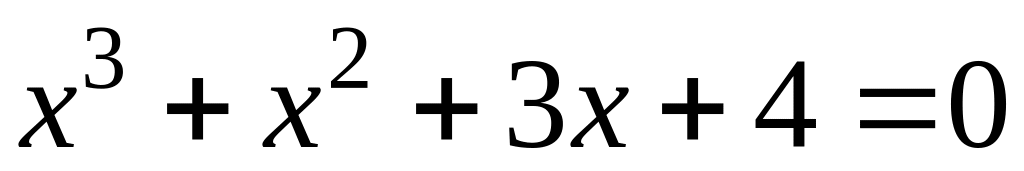7. Спростити вираз:

Тематичні тести тест 1 Подільність. Взаємнопрості многочлени. Нсд та нск многочленів. Раціональні дроби

1. Чи є многочленом від змінної чи вираз:

а) ;

б) ;

в) ;

г) .

2. Який степінь має многочлен :

а) 3;

б) 4;

в) 8;

г) 7.

3. Канонічною формою многочлена називається такий запис:

а) коли його члени впорядковані в довільному порядку;

б) коли його члени впорядковані за спаданням степеня ;

в) коли його члени впорядковані за зростанням степеня ;

г) коли його члени впорядковані за спаданням значення коефіцієнта.

4. Які з многочленів записані в канонічній формі:

а) над полем ;

б) над полем ;

в) над кільцем ;

г) над полем .

5. Допишіть нерівність: …

а) ;

б) ;

в) ;

г) .

6. При яких та многочлен з кільця рівні між собою: та

а) ;

б) ;

в) ;

г) .

7. У кільці многочлени і …, якщо вони відрізняються лише множником, який є відмінною від нуля константою.

а) незвідні;

б) асоційовані;

в) подібні;

г) звідні.

8. Знайти суму коефіцієнтів многочлена 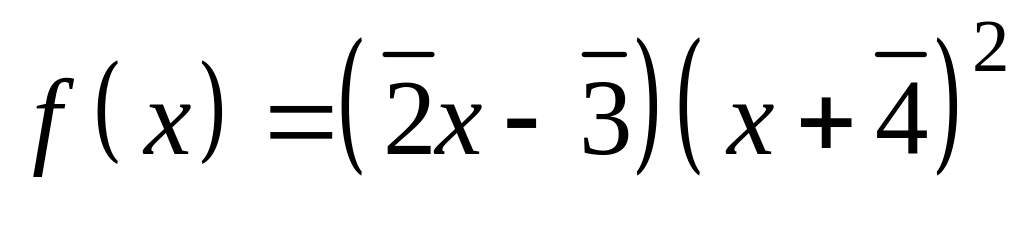з кільця :

а) -5;

б) 24;

в) 0;

г) -25.

9. Як називається многочлен у виразі :

а) ділене;

б) частка;

в) остача;

г) дільник.

10. Як називається вираз виду :

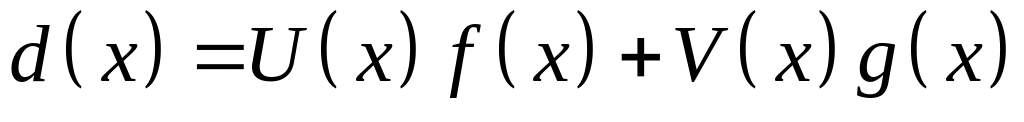а) лінійний запис НСД;

б) лінійний запис НСК;

в) лінійне представлення НСД;

г) лінійне представлення НСК.

11. … називається будь-який многочлен такий, що :

а) СД;

б) НСК;

в) НСД;

г) СК.

12. Якщо , то називається …

а) СД;

б) НСК;

в) НСД;

г) СК.

13. Многочлен називається … у полі , якщо і в кільці існують многочлени і такі, що = , і .

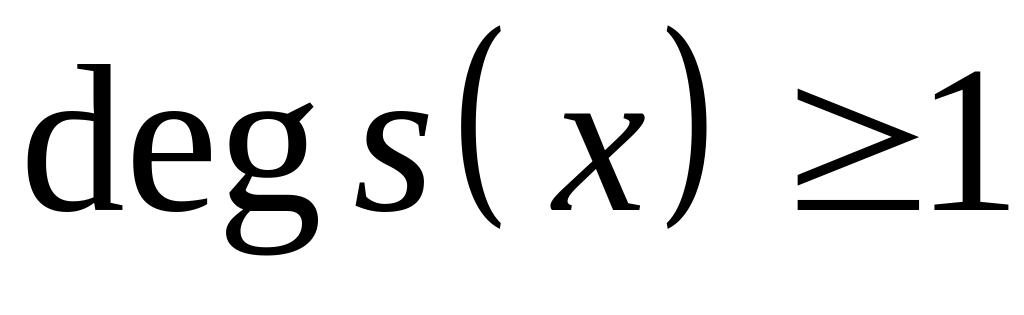а) незвідним;

б) асоційованим;

в) симетричним;

г) звідним.

14. Чи вірне твердження: многочлен першого степеня над будь-яким полем є звідним у кільці ?

а) так;

б) ні;

в) в окремих випадках;

г) можливо.

15. Поле , де многочлен розкладається на лінійні множники називається:

а) канонічним полем;

б) полем розкладу;

в) кратним полем;

г) звідним полем.

16. Якщо , то многочлени і називаються:

а) асоційованими;

б) звідними;

в) незвідними;

г) взаємно простими.

17. Число всіх можливих коренів многочлена степеня над полем …

а) дорівнює ;

б) не перевищує ;

в) більше ;

г) менше .

18. Скільки многочленів можуть бути найменшим спільним дільником многочленів і у кільці :

а) 2;

б) 1;

в) 4;

г) безліч.

19. Скільки многочленів можуть бути найменшим спільним кратним многочленів і у кільці :

а) 2;

б) 1;

в) 4;

г) безліч.

20. Раціональний дріб називається неправильним, якщо …

а) ;

б) ;

в) ;

г) .

21. – це …

а) СД;

б) СК;

в) НСК;

г) НСД.

22. Як називається вираз :

а) канонічний розклад многочлена ;

б) розклад многочлена на множники;

в) лінійне представлення многочлена ;

г) розклад многочлена на незвідні множники.

23. Елементарним дробом у полі називається раціональний дріб виду:

а) , де - звідний у полі , ;

б) , де - незвідний у полі , , ;

в) , де - незвідний у полі , , ;

г) , де - звідний у полі , , ;

24. Який з раціональних дробів є елементарним над полем :

а) ;

б) ;

в) ;

г) .

25. Неправильний дріб над полем можна подати як …

а) суму многочлена і неправильного дробу;

б) різницю многочлена і правильного дробу;

в) суму многочлена і правильного дробу;

г) суму многочленів.

26. Нехай маємо деякий многочлен . Тоді запис означає:

а) - корінь многочлена ;

б) значення многочлена при .

27. Нехай є довільний многочлен . Що розуміється під записом :

а) - корінь многочлена ;

б) значення многочлена при .