§ 11. Відокремлення дійсних коренів многочленів. Теорема Штурма Питання для самоконтролю:

1. Як розташовані комплексні корені з дійсними коефіцієнтами відносно дійсної осі?

2. Де розміщені всі дійсні корені рівняння ?

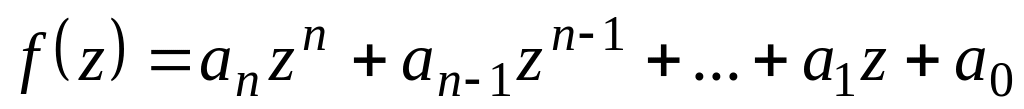3. Число М є верхньою межею додатних коренів многочлена , якщо …

4. Кількість змін знаків деякої впорядкованої послідовності дійсних чисел – це …

5. Сформулюйте правило Декарта.

6. Яка заміна використовується для знаходження кількості від’ємних коренів многочлена ?

7. Щоб побудувати ряд Штурма необхідно…

8. Сформулювати теорему Штурма.

9. Чи мають дві сусідні функції ряду Штурма спільні корені?

10. Якщо є коренем однієї з проміжних функцій ряду Штурма, то…

11. Якщо , зростаючи, проходить через корінь якої-небудь проміжної функції ряду, але не проходить через корінь , то …

12. Якщо , зростаючи, проходить через корінь многочленна , то…

Задачі

1) Знайти верхню межу дійсних коренів многочлена методом Ньютона:

2) Знайти нижню межу дійсних коренів многочлена методом Ньютона:

3) Обмежити зверху і знизу дійсні корені многочленів:

4) Знайти число дійсних коренів для многочленів: на проміжку [0,2], на проміжку [-3,5].

5) Відокремити дійсні корені многочленів:

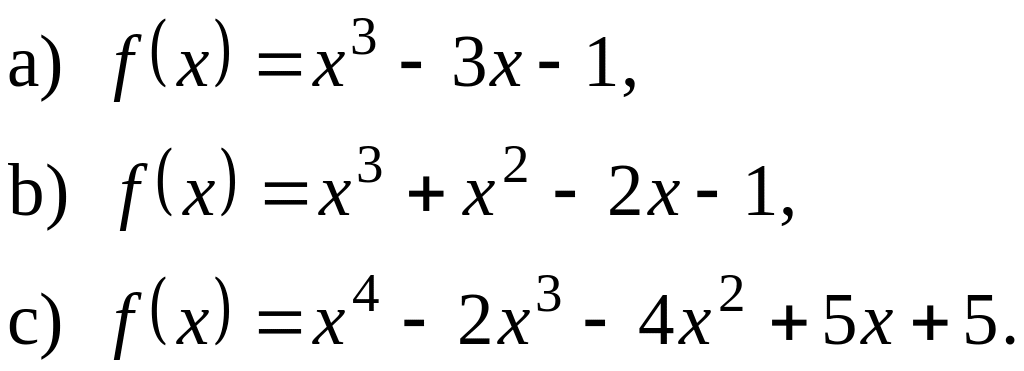
6) Оцінити за правилом Декарта число додатніх і від’ємних коренів многочлена

Розділ IV. Многочлени над полем раціональних чисел та алгебраїчні числа § 12. Цілі і раціональні корені многочлена з цілими коефіцієнтами. Критерій незвідності Ейзенштейна Питання для самоконтролю:

1. Число якого виду може бути раціональним коренем многочлена?

2. При якій умові число , де 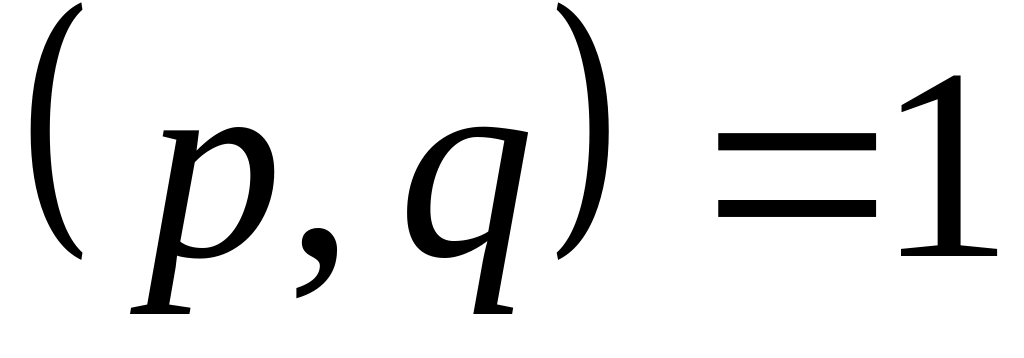, може бути коренем рівняння з цілими коефіцієнтами?

3. Коли всі раціональні корені є цілими числами і являються дільниками вільного члена?

4. Якщо числа 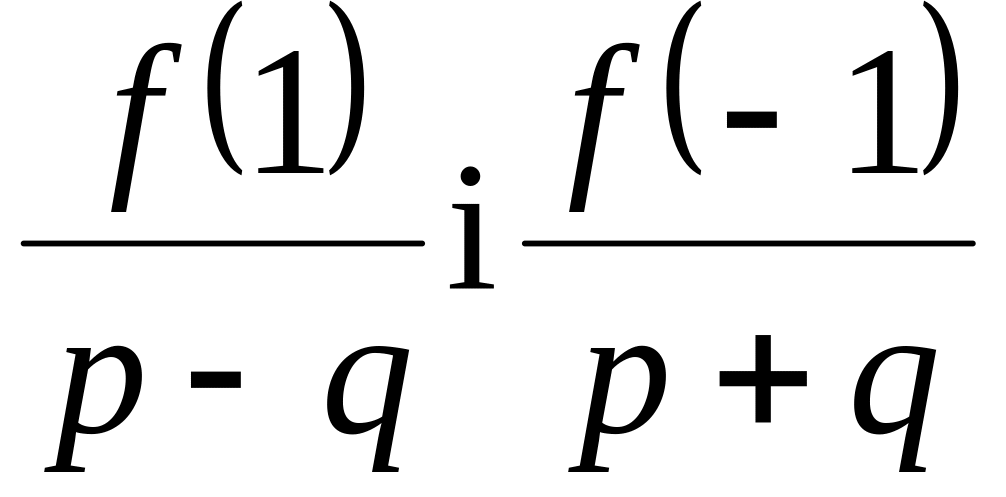є цілими, то є …

5. Умова звідності многочлена з цілими коефіцієнтами у полі раціональних чисел.

6. Якщо многочлен з раціональними коефіцієнтами, 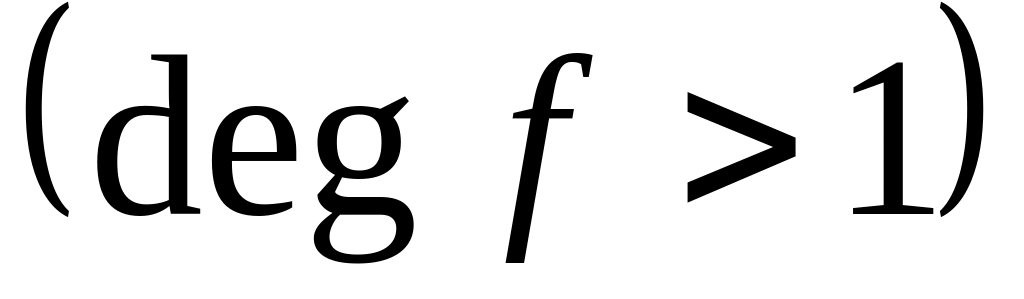має хоч один раціональний корінь 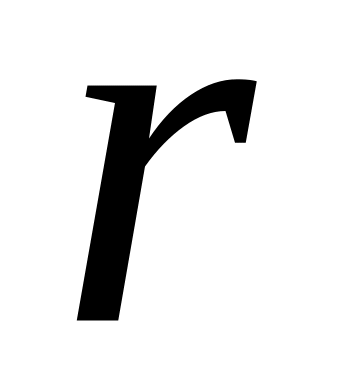, то …

7. Сформулюйте критерій Ейзенштейна незвідності многочлена з цілими коефіцієнтами.

Задачі

1. Розв’язати рівняння:

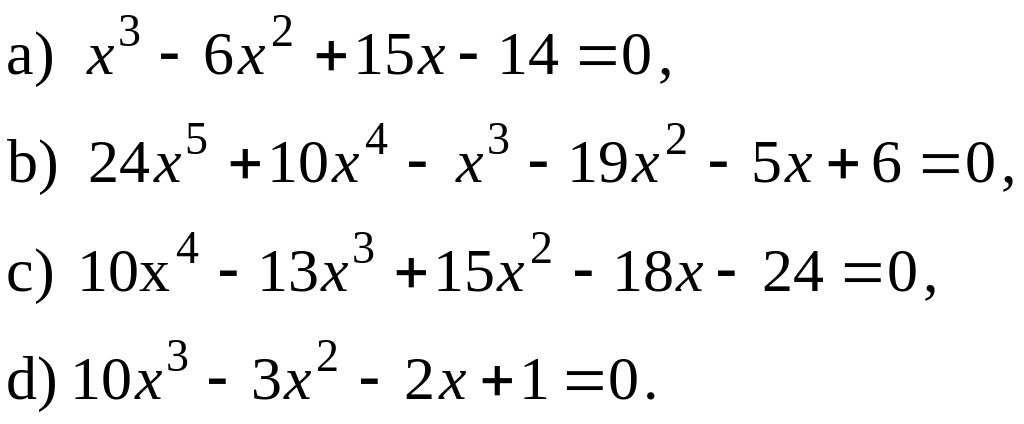
2. Знайти раціональні корені рівняння:

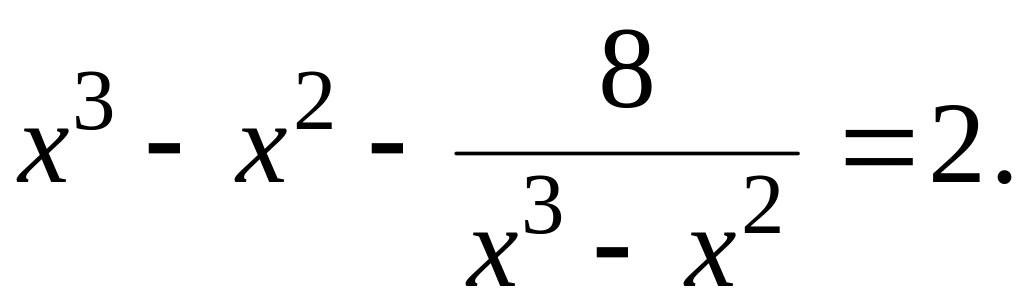
3. Розкласти на незвідні множники дані многочлени або довести їх незвідність:

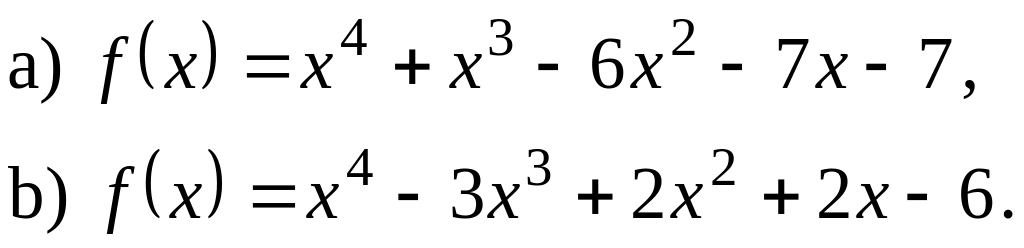
4. Дослідити на звідність у полі Q такий многочлен:

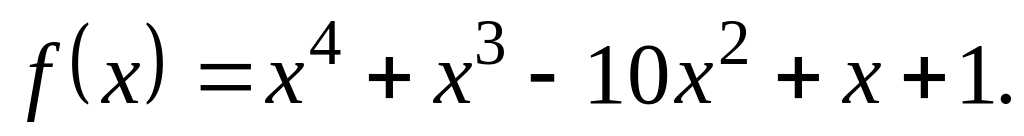
5. Що можна сказати про звідність даного многочлена у кільці :

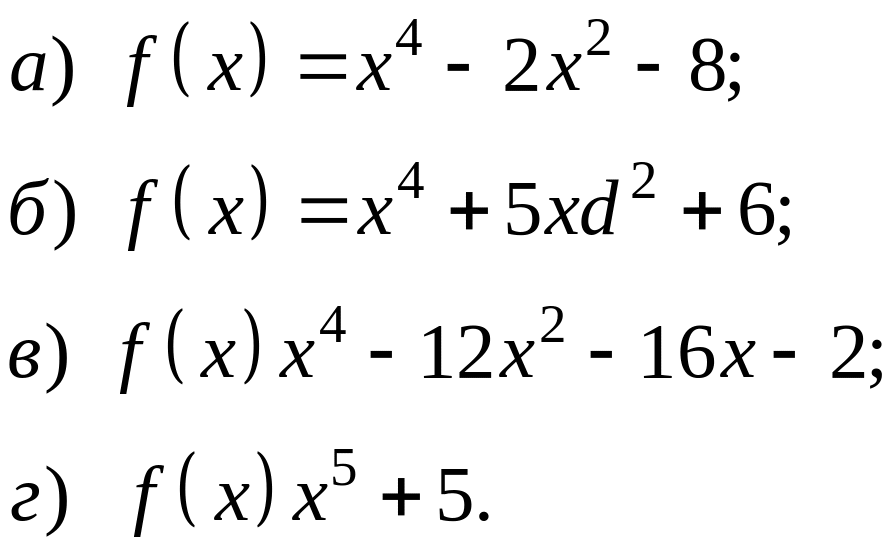
6. Користуючись критерієм Ейзенштейна, довести незвідність над полем Q многочленів:

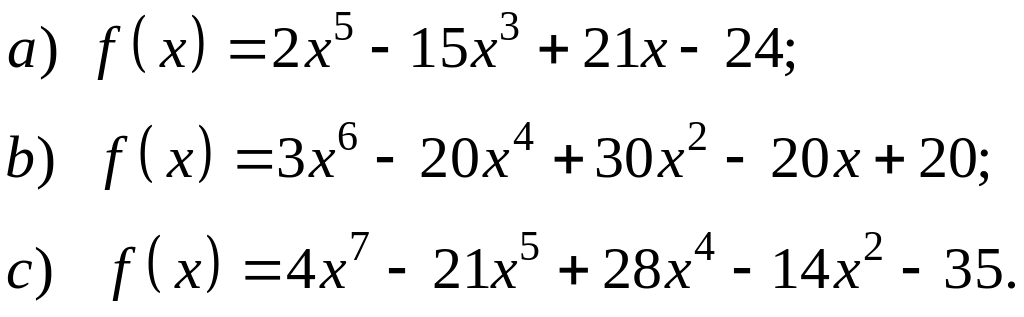
§ 13. Алгебраїчні і трансцендентні числа. Будова простого алгебраїчного розширення поля Питання для самоконтролю:

1. Яке число називається алгебраїчним відносно поля ? А яке трансцендентним?

2. Чи існує незвідний зведений многочлен , коренем якого є алгебраїчне число відносно поля ? Який його степінь? Як він називається? Скільки таких многочленів існує?

3. Яке поле називається простим алгебраїчним (трансцендентним) розширенням поля ?

4. З яких чисел складається поле 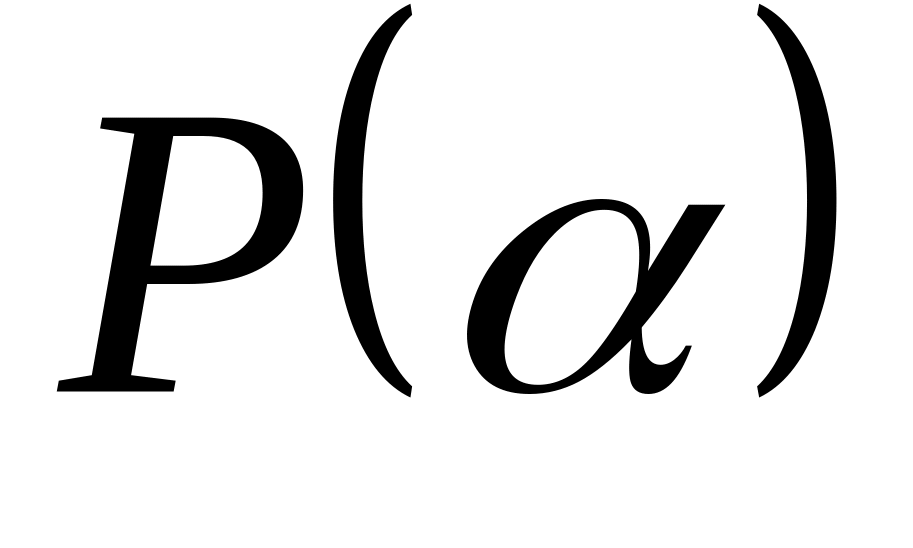, утворене з поля приєднанням кореня α, незвідного у полі многочлена -го степеня ?

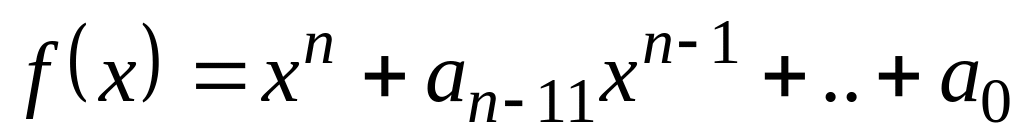5. З яких чисел складається просте алгебраїчне розширення Р(α) поля , якщо α – корінь многочлена 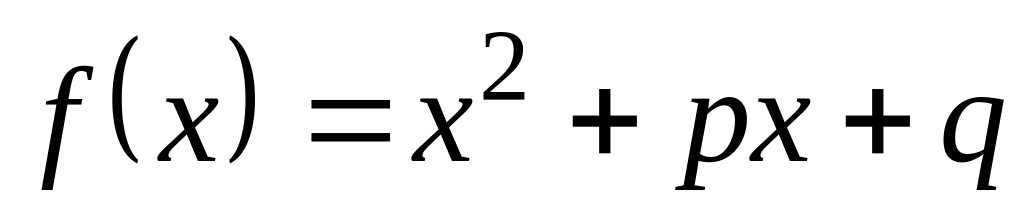і ?

6. Яке розширення поля називається квадратичним?

7. Розширення поля називається скінченим, якщо …

8. Яка степінь будь-якого квадратичного розширення?

9. Яке розширення є складним розширенням поля ?

10. Якщо всі елементи поля є алгебраїчними відносно поля , то розширення називається …

Задачі

1. Довести, що число  є алгебраїчним і знайти його мінімальний многочлен:

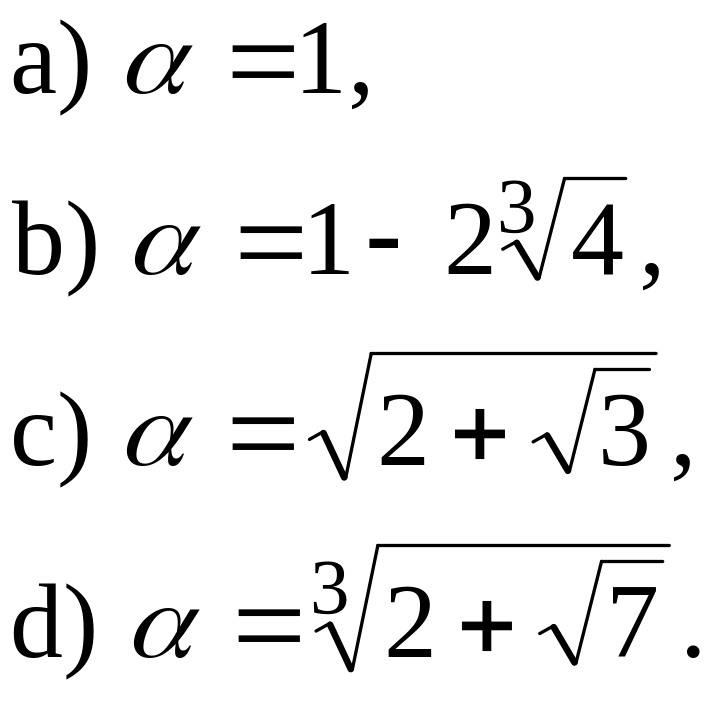
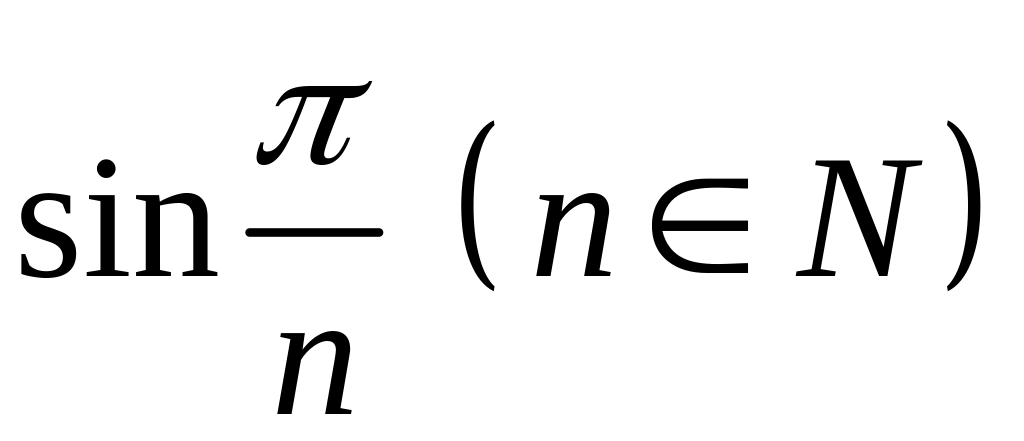2. Довести, що числа і алгебраїчні. Знайти степінь числа .

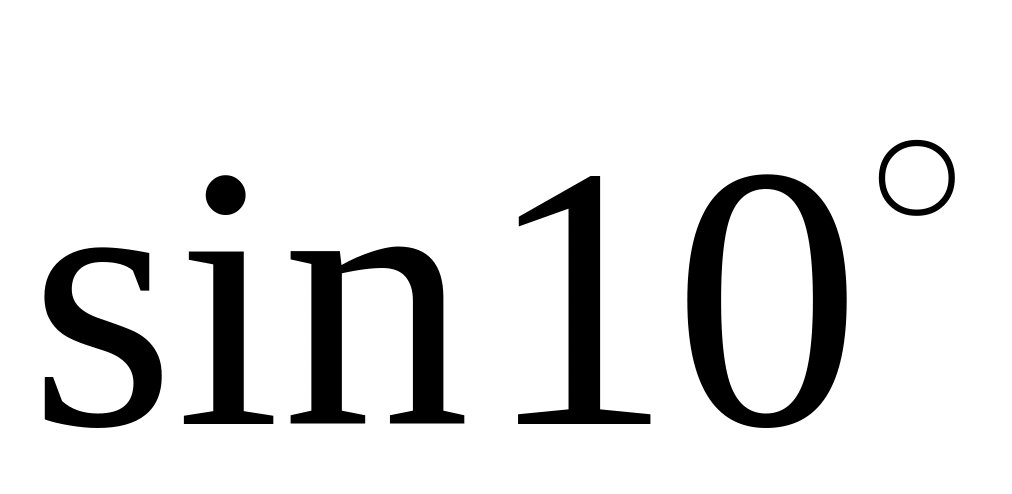3. Довести безпосередньо, що число є алгебраїчним, і знайти многочлен над Q (не обов’язково мінімальний), коренем якого є :

4. Для даного числа , алгебраїчного над Q, знайти алгебраїчно спряжене до нього (над Q) число:

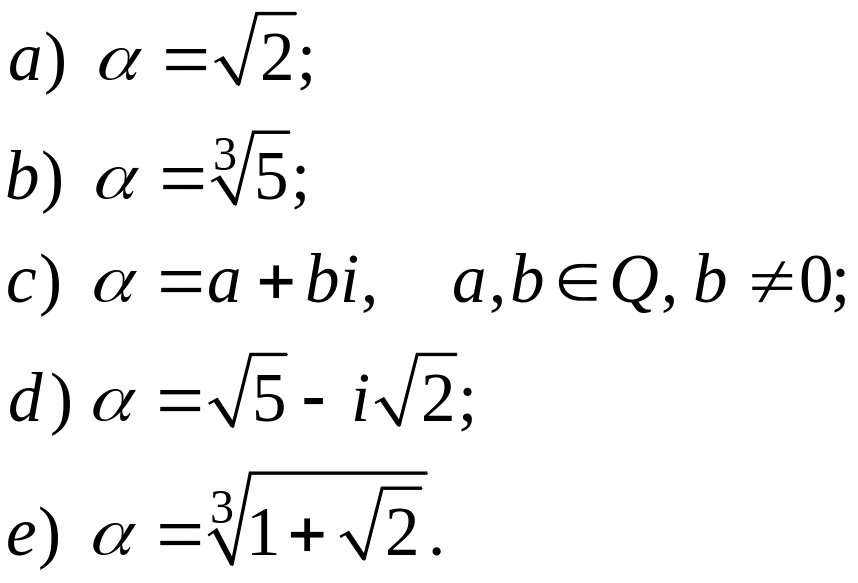
5. Чи міститься в полі число 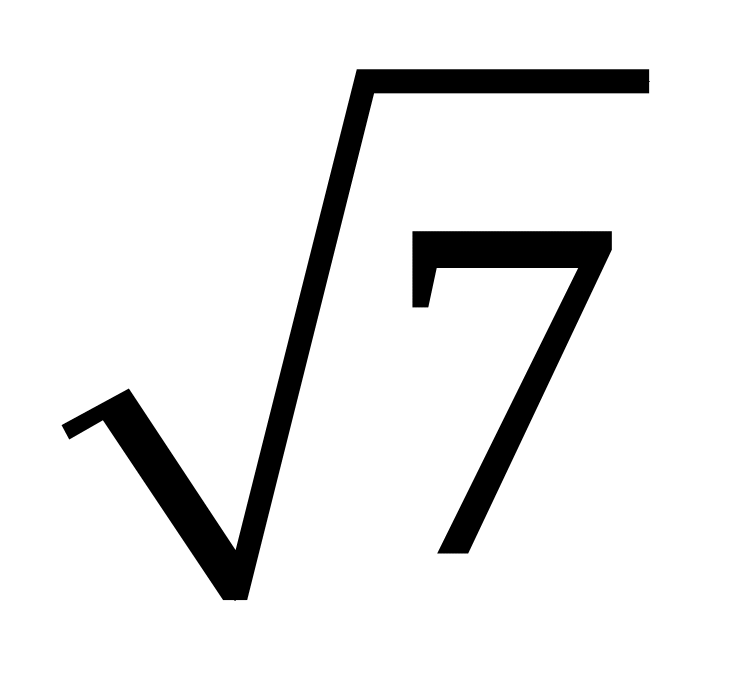? В полі 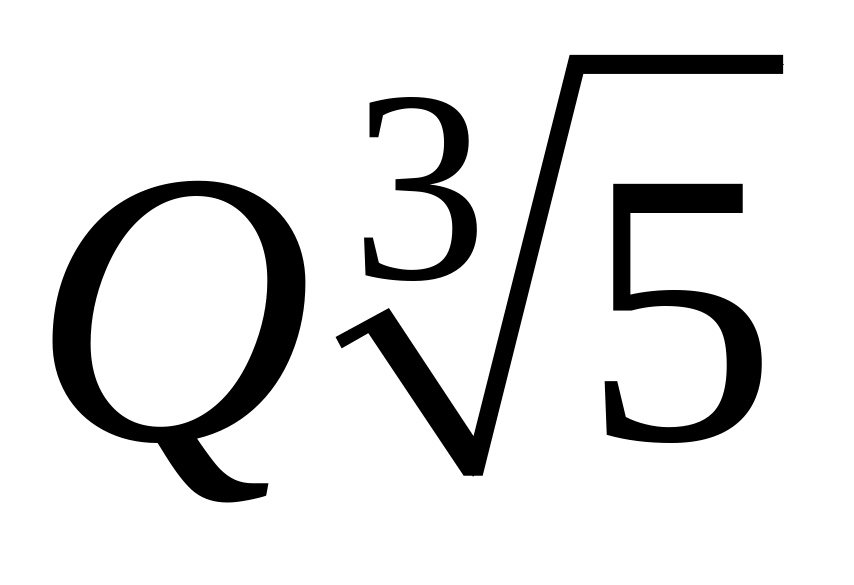число ?

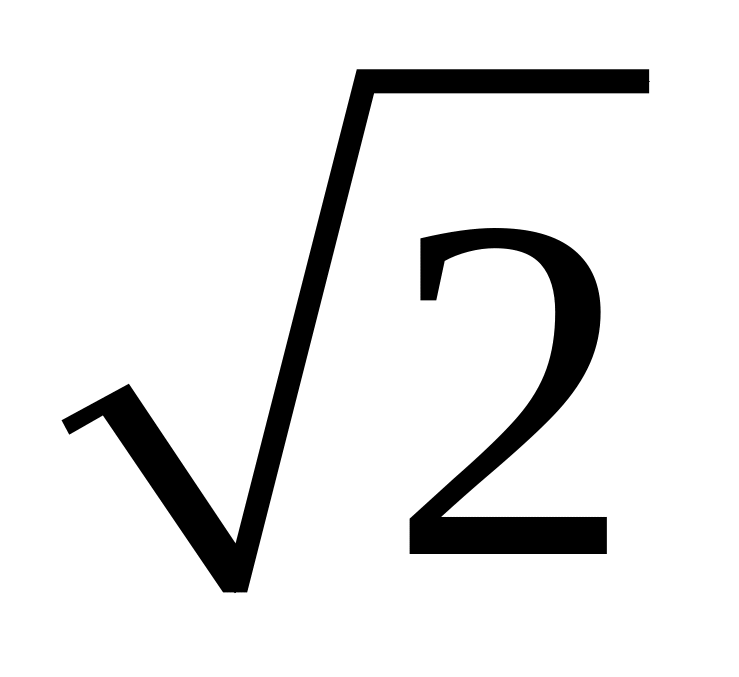6. Знайти алгебраїчне число, приєднанням якого до Q поля можна дістати складне алгебраїчне розширення:

де - прості числа,

,

.

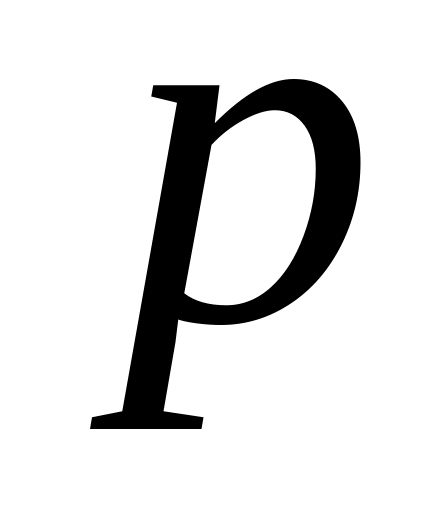7. Нехай і - натуральні числа, причому 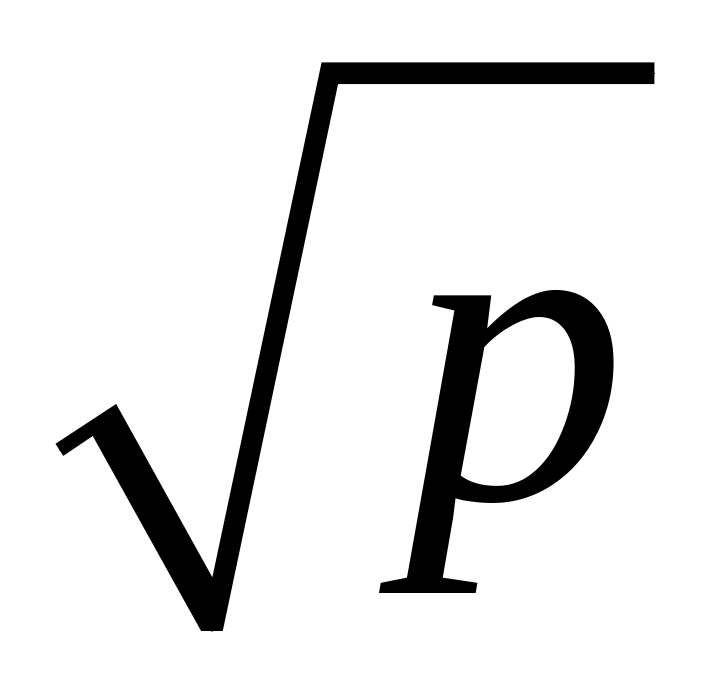і 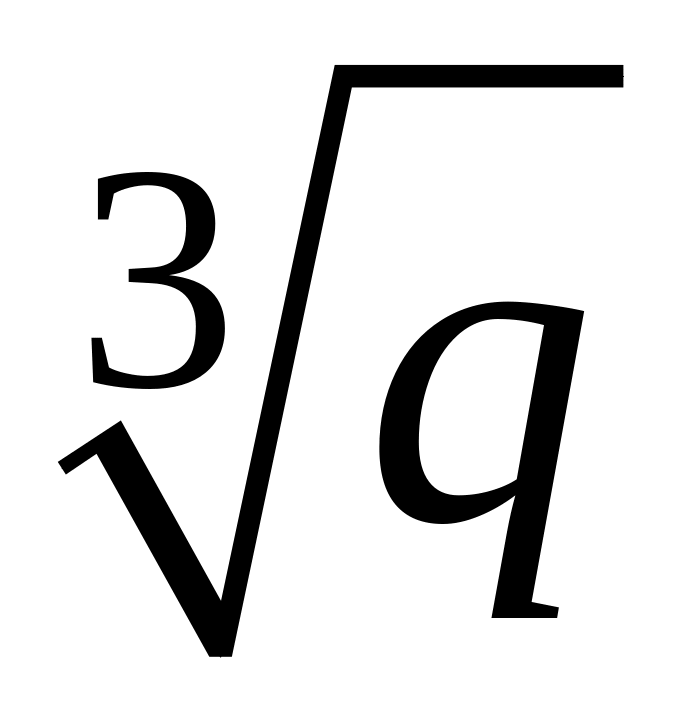- не цілі. Довести, що .

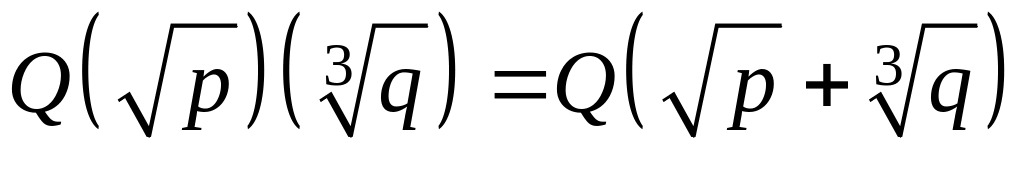8. Знайти вираження для кожного з чисел і через + :