
- •§ 3. Незвідні многочлени над полем. Розклад многочленів на незвідні множники. Похідна многочлена. Кратні корені Питання для самоконтролю:
- •§ 4. Раціональні дроби. Елементарні дроби. Розклад дробу на елементарні дроби над полями q,r і c Питання для самоконтролю:
- •Розділ II. Многочлени від кількох змінних § 5. Кільце многочленів від n змінних. Розклад многочлена на добуток незвідних множників. Симетричні многочлени Питання для самоконтролю:
- •§ 6. Застосування симетричних многочленів до розв’язування деяких задач з елементарної алгебри Задачі
- •§ 7. Дискримінант та результант двох многочленів, їх властивості і застосування до розв'язування задач Питання для самоконтролю:
- •Розділ III.Многочлени над полем комплексних чисел і над полем дійсних чисел § 8. Многочлени над полем комплексних чисел. Алгебраїчна замкненість поля комплексних чисел Питання для самоконтролю:
- •§ 9. Многочлени над полем дійсних чисел Питання для самоконтролю:
- •§ 10. Рівняння третього степеня Питання для самоконтролю:
- •§ 11. Відокремлення дійсних коренів многочленів. Теорема Штурма Питання для самоконтролю:
- •Розділ IV. Многочлени над полем раціональних чисел та алгебраїчні числа § 12. Цілі і раціональні корені многочлена з цілими коефіцієнтами. Критерій незвідності Ейзенштейна Питання для самоконтролю:
- •§ 13. Алгебраїчні і трансцендентні числа. Будова простого алгебраїчного розширення поля Питання для самоконтролю:
- •§ 14. Позбавлення від алгебраїчної ірраціональності в знаменнику дробу Питання для самоконтролю:
- •Тематичні тести тест 1 Подільність. Взаємнопрості многочлени. Нсд та нск многочленів. Раціональні дроби
- •Чи вірно, що коли многочлени рівні між собою функціонально, то вони рівні і алгебраїчно?
- •Тест 2 Симетричні многочлени
- •Тест 3 Многочлени над різними полями
- •Тест 4 Алгебраїчні розширення
- •Підсумковий тест Теорія многочленів
- •Відповіді Розділ I
- •Розділ II
- •Розділ III
- •Розділ IV
- •Тест II
- •Тест III
- •Тест IV
- •Список використаних джерел.
Розділ III.Многочлени над полем комплексних чисел і над полем дійсних чисел § 8. Многочлени над полем комплексних чисел. Алгебраїчна замкненість поля комплексних чисел Питання для самоконтролю:
Яке поле називається алгебраїчно замкненим?
Скільки дійсних і комплексних коренів має многочлен з дійсними коефіцієнтами?
Сформулюйте основну теорему теорії многочленів.
Які многочлени називаються звідними у полі комплексних чисел?
Необхідна і достатня умова незвідності многочлена у полі С: …
Скільки коренів має многочлен -го степеня у полі комплексних чисел?
Задачі
1) Знайти
многочлен найменшого степеня, в
якого:
а) 1 – подвійний корінь, а 2, 3,
![]() – прості;
б) -1
– потрійний корінь, а 3 і 4 – прості.
– прості;
б) -1
– потрійний корінь, а 3 і 4 – прості.
2) Знайти
многочлен найменшого степеня з дійсними
коефіцієнтами, якщо
![]() – його потрійний корінь.
– його потрійний корінь.
3) Знайти
суму квадратів коренів многочлена
![]()
Сума двох коренів рівняння
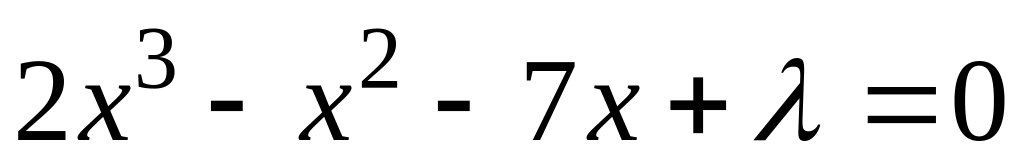 дорівнює
1. Визначити
.
дорівнює
1. Визначити
.Використовуючи формули Вієта, побудувати многочлен за його коренями:
![]()
Знайти зведений многочлен, в якого корені задовольняють умову:
 ,
а
,
а
 ,
, ,
, є коренями многочлена
є коренями многочлена
 .
.Корені многочлена утворюють арифметичну прогресію. Знайти цей многочлен і його корені, якщо
 .
.Чи утворюють корені рівняння
 арифметичну прогресію?
арифметичну прогресію?Визначте так, щоб один з коренів многочлена був рівний подвоєному другому кореню.
§ 9. Многочлени над полем дійсних чисел Питання для самоконтролю:
Що можна сказати про спряжене комплексне число
 ,
якщо комплексне число
,
якщо комплексне число
 є коренем многочлена
є коренем многочлена
 з дійсними коефіцієнтами?
з дійсними коефіцієнтами?Який многочлен є звідним у полі дійсних чисел?
Як можна многочлен розкласти над полем дійсних чисел на незвідні множники?
Задачі
Розв’язати рівняння:
![]() ,
якщо
,
якщо
![]() ;
;
![]() ,
якщо
,
якщо
![]() ;
;
![]() ,
якщо
,
якщо
![]() .
.
2) Знайти нормований многочлен найменшого степеня з дійсними коефіцієнтами, що має:
а)
простий корінь
![]() і двократний корінь 1;
і двократний корінь 1;
b)
простий корінь
![]() і двократні корені
і двократні корені
![]() та
та
![]() ;
;
с) трикратний корінь .
3) Знаючи, що число є коренем многочлена , знайти інші його корені:

Розкласти многочлен на множники, незвідні над полем R:

Яким умовам повинні задовольняти дійсні коефіцієнти многочлена:
![]() ,
щоб він мав два різних дійсних корені;
,
щоб він мав два різних дійсних корені;
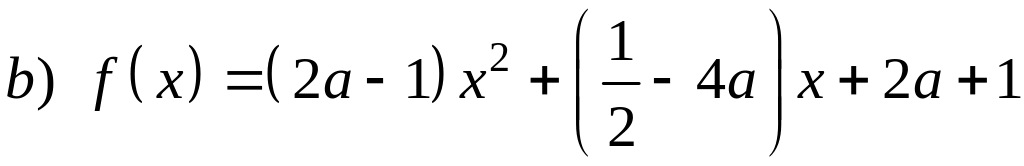 ,
щоб він мав один дійсний корінь.
,
щоб він мав один дійсний корінь.
§ 10. Рівняння третього степеня Питання для самоконтролю:
Яке рівняння називається рівнянням третього степеня?
Рівняння
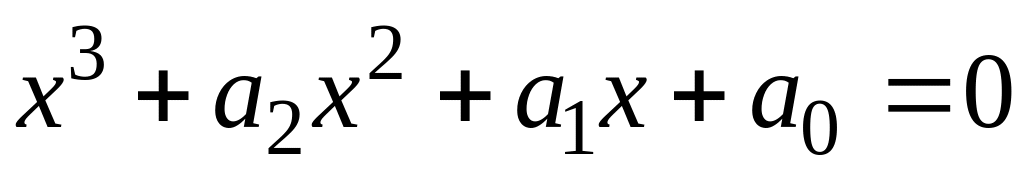 третього степеня зводиться до рівняння
виду
третього степеня зводиться до рівняння
виду
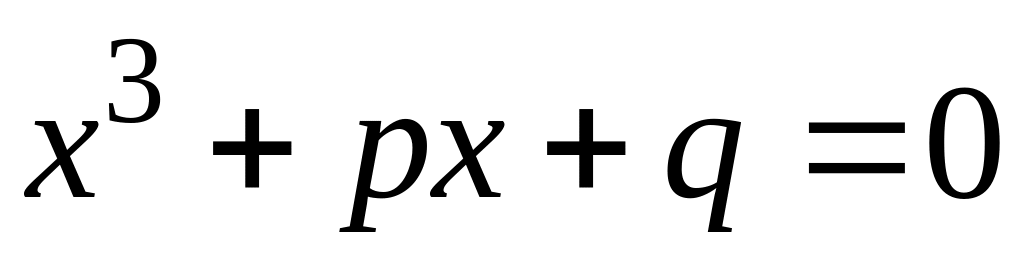 за допомогою …
за допомогою …Як називається вираз
 ?
?Як знайти корені рівняння ?
Коли рівняння має один дійсний і два комплексні корені спряжених?
Якщо
 ,
то які корені має рівняння
?
,
то які корені має рівняння
?Рівняння має три дійсні корені, якщо …
U1 i V1 – це …
З якої умови знаходиться числа U1 i V1?
Задачі
Звести кубічне рівняння до виду, у якому відсутній доданок з невідомим у другому степені:
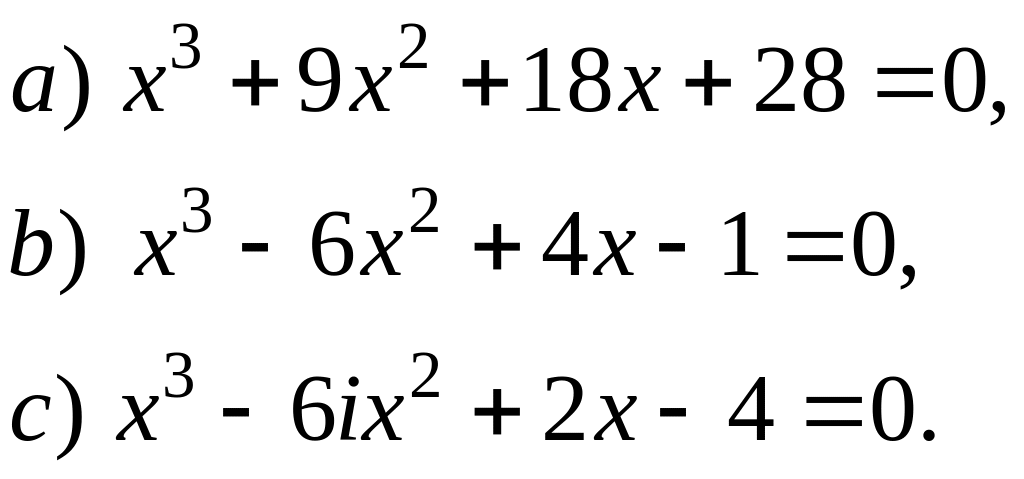
Розв’язати рівняння :
![]()
![]()
![]()
При яких дійсних значеннях рівняння
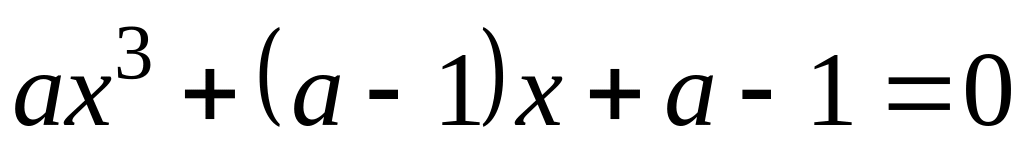 має кратний корінь? Знайти його.
має кратний корінь? Знайти його.Які корені залежно від значення числа має рівняння з дійсними коефіцієнтами
 ?
?Розв’язати рівняння
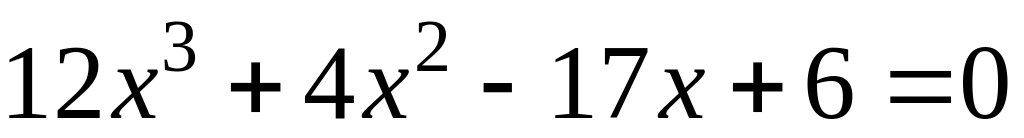 ,
коли відомо, що серед його коренів є
два числа, обернених за абсолютною
величиною і протилежних за знаком.
,
коли відомо, що серед його коренів є
два числа, обернених за абсолютною
величиною і протилежних за знаком.Розв’язати рівняння
 ,
коли відомо, що добуток двох його коренів
дорівнює 1.
,
коли відомо, що добуток двох його коренів
дорівнює 1.Розв’язати кубічне рівняння
 ,
коли відомо, що його коефіцієнти в
порядку спадання степенів утворюють
геометричну прогресію з знаменником
2.
,
коли відомо, що його коефіцієнти в
порядку спадання степенів утворюють
геометричну прогресію з знаменником
2.
