
- •§ 3. Незвідні многочлени над полем. Розклад многочленів на незвідні множники. Похідна многочлена. Кратні корені Питання для самоконтролю:
- •§ 4. Раціональні дроби. Елементарні дроби. Розклад дробу на елементарні дроби над полями q,r і c Питання для самоконтролю:
- •Розділ II. Многочлени від кількох змінних § 5. Кільце многочленів від n змінних. Розклад многочлена на добуток незвідних множників. Симетричні многочлени Питання для самоконтролю:
- •§ 6. Застосування симетричних многочленів до розв’язування деяких задач з елементарної алгебри Задачі
- •§ 7. Дискримінант та результант двох многочленів, їх властивості і застосування до розв'язування задач Питання для самоконтролю:
- •Розділ III.Многочлени над полем комплексних чисел і над полем дійсних чисел § 8. Многочлени над полем комплексних чисел. Алгебраїчна замкненість поля комплексних чисел Питання для самоконтролю:
- •§ 9. Многочлени над полем дійсних чисел Питання для самоконтролю:
- •§ 10. Рівняння третього степеня Питання для самоконтролю:
- •§ 11. Відокремлення дійсних коренів многочленів. Теорема Штурма Питання для самоконтролю:
- •Розділ IV. Многочлени над полем раціональних чисел та алгебраїчні числа § 12. Цілі і раціональні корені многочлена з цілими коефіцієнтами. Критерій незвідності Ейзенштейна Питання для самоконтролю:
- •§ 13. Алгебраїчні і трансцендентні числа. Будова простого алгебраїчного розширення поля Питання для самоконтролю:
- •§ 14. Позбавлення від алгебраїчної ірраціональності в знаменнику дробу Питання для самоконтролю:
- •Тематичні тести тест 1 Подільність. Взаємнопрості многочлени. Нсд та нск многочленів. Раціональні дроби
- •Чи вірно, що коли многочлени рівні між собою функціонально, то вони рівні і алгебраїчно?
- •Тест 2 Симетричні многочлени
- •Тест 3 Многочлени над різними полями
- •Тест 4 Алгебраїчні розширення
- •Підсумковий тест Теорія многочленів
- •Відповіді Розділ I
- •Розділ II
- •Розділ III
- •Розділ IV
- •Тест II
- •Тест III
- •Тест IV
- •Список використаних джерел.
Міністерство освіти України
Черкаський національний університет
ім. Богдана Хмельницького
Ілляшенко Н.Г.
Гордієнко Н.М.
Теорія многочленів
Частина II
Черкаси 2005р.
Міністерство освіти України
Черкаський національний університет
ім. Богдана Хмельницького
Ілляшенко Н.Г.
Гордієнко Н.М.
Теорія многочленів
Частина II
Навчально – методичний посібник для організації самостійної роботи студентів
Черкаси 2005р.
Посібник містить набір запитань для самоперевірки відповідно до розділів частини І. Запропоновано 97 завдань для самостійної роботи. До кожної задачі дано відповідь.
Посібник призначений для організації самостійної роботи студентів стаціонарної та заочної форм навчання.
Рецензент : Кляцька Л. М. – кандидат фіз-мат наук, доцент кафедри алгебри, геометрії та МВМ ЧНУ ім. Б. Хмельницького.
Розділ I. Многочлени від однієї змінної
§ 1. Кільце многочленів. Алгебраїчна і функціональна рівність многочленів. Відношення подільності в кільці многочленів. Ділення з остачею
Питання для самоконтролю:
Многочлен – це …
Старший коефіцієнт многочлена – це … , старший член многочлена – це … , степінь многочлена – це … .
Чи є такий запис многочлена його канонічною формою. Відповідь пояснити.



Канонічне представлення многочлена єдине чи ні?
Чому рівний степінь суми та добутку многочлена?
Що означають записи
 і
і

В чому полягає функціональна рівність многочленів?
Яка умова алгебраїчної рівності многочленів?
Чи вірно, що коли многочлени рівні між собою функціонально, то вони рівні і алгебраїчно?
Асоційовані многочлени – це …
Що означає запис:
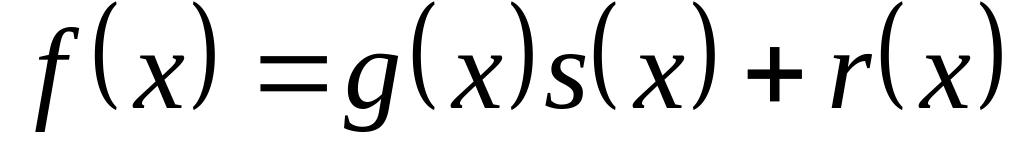
Задачі
Знайти канонічну форму многочлена:
а)
![]() в кільці
в кільці![]() ;
;
б)
![]() у кільці
у кільці
![]() .
.
Виконати ділення з остачею („кутом”): а) многочлена
 на многочлен
на многочлен
 ;
б)
многочлена
;
б)
многочлена
 на многочлен
на многочлен
 .
.Використовуючи схему Горнера поділити в кільці
 многочлен
многочлен
 на лінійний двочлен
на лінійний двочлен
 :
а)
:
а)
 ;
б)
;
б)
 .
.При якій умові многочлен
 ділиться на многочлен
ділиться на многочлен
 .
.При яких значеннях
 многочлени
многочлени
 і
і
 з
кільця
з
кільця
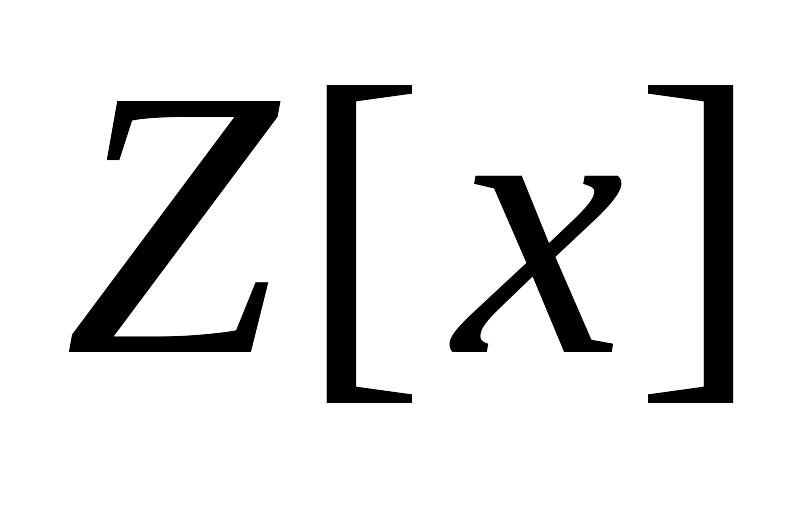 рівні
між собою:
рівні
між собою:
 .
.Довести, що з функціональної точки зору ці многочлени рівні:
![]() з кільця
з кільця
![]() .
.
Знайти всі значення
 при
яких многочлен
є
квадратом
при
яких многочлен
є
квадратом
деякого
многочлена
з кільця
![]() .
Записати
.
Записати
![]() .
.
![]() .
.
Знайти суму коефіцієнтів многочленна
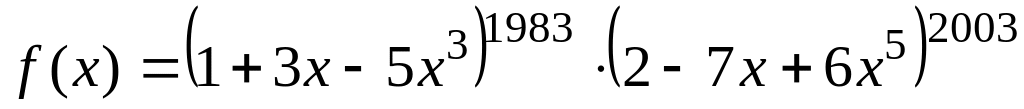 в кільці
.
в кільці
.Знайти необхідну і достатню умову подільності многочленів
 на
на
 в
кільці
.
в
кільці
.Знайти остачу від ділення
 на
на
 в кільці
.
в кільці
.При діленні многочлена
 на
в
кільці
дістали остачу
на
в
кільці
дістали остачу
 .
Знайти остачу від ділення
.
Знайти остачу від ділення
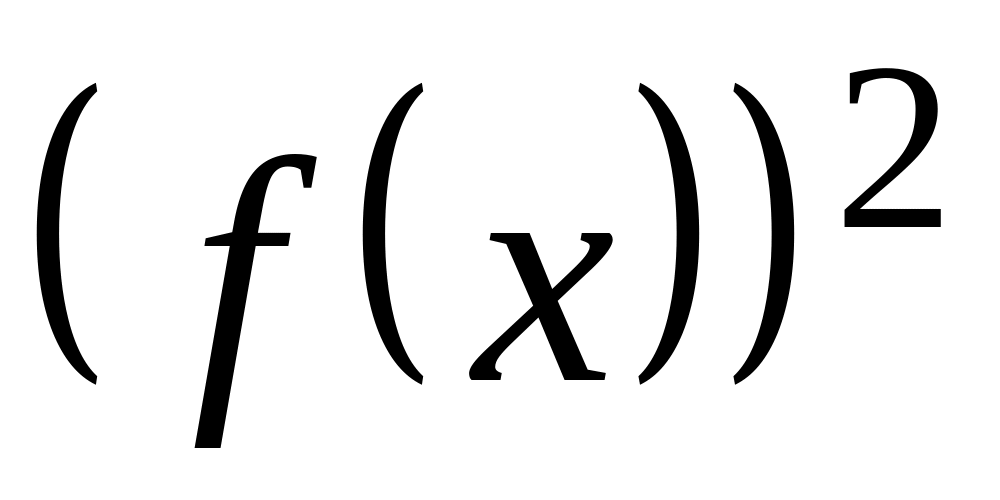 на
на
 ,
якщо
,
якщо
 .
.При діленні многочлена на в кільці
 дістали остачу 3, а при діленні
дістали остачу 3, а при діленні
 на
на
 - остачу 9. Яка буде остача, якщо
поділити
на
- остачу 9. Яка буде остача, якщо
поділити
на
 ?
?При діленні многочлена на
 у кільці
у кільці
 дістали частку
дістали частку
 та остачу
та остачу
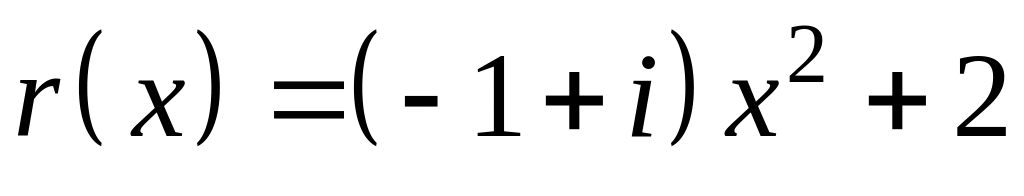 .
Знайти остачу від ділення
на
.
Знайти остачу від ділення
на
 .
.
§ 2. Ділення многочлена на двочлен ( x- ). Теорема Безу. Схема Горнера. Розклад многочлена за степенями ( x-). Найбільший спільний дільник і найменше спільне кратне многочленів. Алгоритм Евкліда
Питання для самоконтролю:
Сформулювати теорему Безу і наслідок з неї.
Що означає розкласти многочлен за степенями
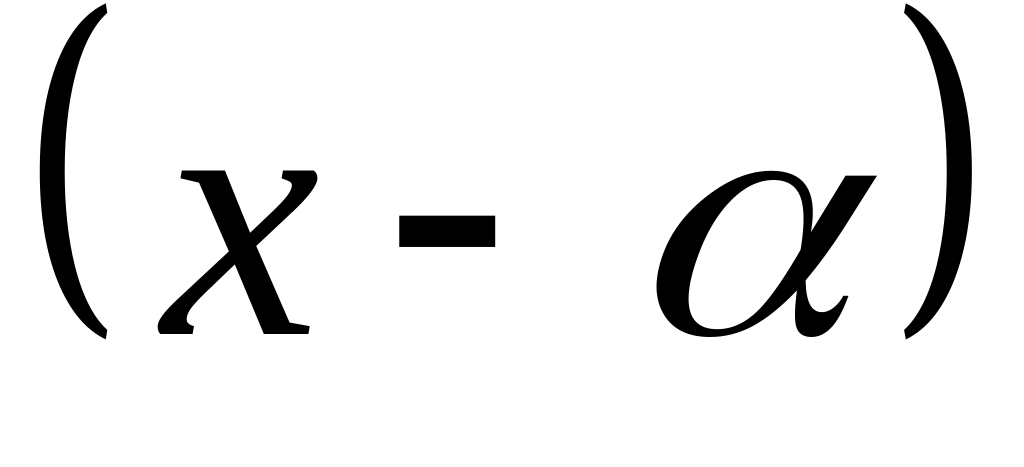 ?
?Який дільник є спільним для многочленів?
Спільний дільник називається найбільшим спільним дільником многочленів, якщо…
Взаємно прості многочлени – це…
Що означає лінійно представити найбільший спільний дільник ?
При якій умові і взаємно прості?
Алгоритм Евкліда. Для чого його використовують?
Спільне кратне многочленів і - це …
Що називається НСК многочленів і як його обчислити?
Задачі
Знайти частку і остачу від ділення многочлена
 на многочлен
на многочлен
 .
.Знайти значення многочлена з кільця
 в точці
в точці
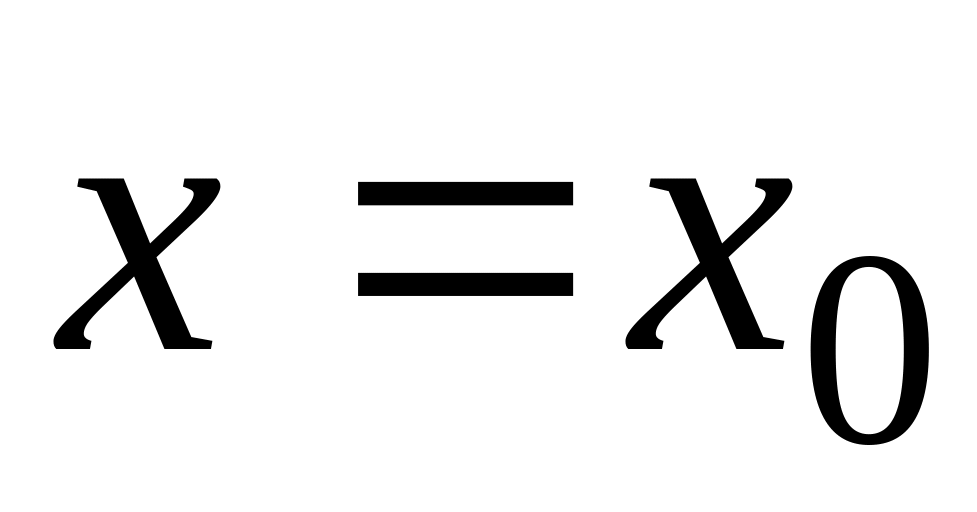 ,
якщо:
,
якщо:
а)
![]() К
= С
;
К
= С
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
3) Методом
невизначених коефіцієнтів знайти частку
і остачу від ділення
![]() на
на
![]() .
.
4) Остачі
від ділення многочлена
з кільця
на
![]() відповідно дорівнюють
відповідно дорівнюють
![]() .
Знайти остачу від ділення цього многочлена
на
.
Знайти остачу від ділення цього многочлена
на
![]() .
.
При діленні многочлена на

 отримали
остачі 5, -4, 6 відповідно. Знайдіть остачу
при діленні многочлена
на
отримали
остачі 5, -4, 6 відповідно. Знайдіть остачу
при діленні многочлена
на
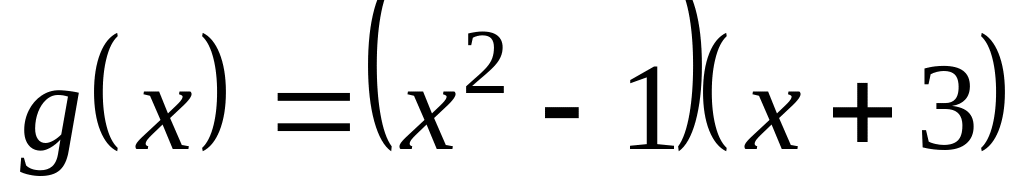 .
.Знайти остачу від ділення многочлена
 на двочлени :
а)
на двочлени :
а)
 б)
б)
 в)
в)

7) Користуючись
схемою Горнера розкласти многочлен
за степенями двочлена
![]() ,
якщо
,
якщо
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
8) Довести,
що многочлен
![]() ділиться:
ділиться:
а) на
![]() над
областю цілісності К з одиницею;
б)
на
над
областю цілісності К з одиницею;
б)
на
![]() в
кільці
в
кільці
![]() .
.
9) Користуючись алгоритмом Евкліда, знайти найбільший спільний дільник таких многочленів:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
10) Знайти
найменше спільне кратне таких многочленів
:
а)
![]() ;
б)
;
б)
![]() ;
в)
.
;
в)
.
11) Визначити
многочлени
![]() і
і
![]() так,
щоб для многочленів
і
виконувалася рівність
так,
щоб для многочленів
і
виконувалася рівність
![]() ,
якщо
,
якщо
а)
![]() ;
б)
;
б)
![]() .
.
§ 3. Незвідні многочлени над полем. Розклад многочленів на незвідні множники. Похідна многочлена. Кратні корені Питання для самоконтролю:
Який многочлен називається незвідним у полі
 ?
?Звідний многочлен у полі – це …
Чи вірно, що многочлени першого степеня над будь-яким
полем
![]() є незвідними у кільці
?
є незвідними у кільці
?
Нехай
 - незвідні многочлени у полі
.
Як називається такий запис:
- незвідні многочлени у полі
.
Як називається такий запис:
 ?
?Канонічним розкладом многочлена називається …
Властивості незвідних многочленів: …
Які множники називаються кратними?
Яка кратність множника
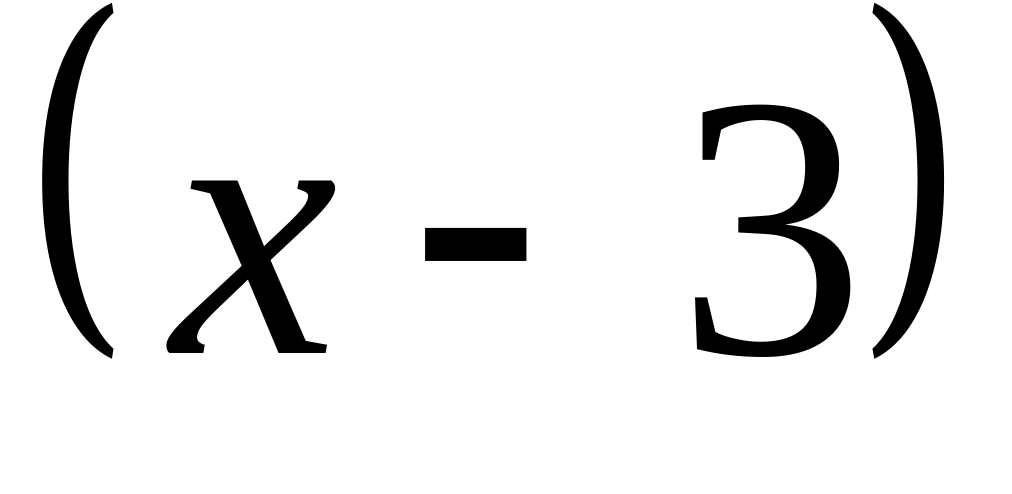 у канонічному розкладі многочлена
у канонічному розкладі многочлена
 ?
?Якщо многочлени і розкладені на незвідні множники у полі , то чому рівний НСД цих многочленів?
Коренем кратності
 називається …
називається …Число коренів многочлена над полем Р рівне …
Що називається полем розкладу многочлена?
Сформулюйте теорему Вієта.
Похідна многочлена
 дорівнює:…
дорівнює:…Чи вірно, що
 ?
?Необхідна і достатня умова, щоб многочлен мав кратний корінь …
Задачі
Встановити чи звідні над полем Q такі многочлени :

Розкласти на незвідні множники многочлен
 в полях Q, R, C, якщо він має дві пари
коренів у полі, які є протилежними
числами.
в полях Q, R, C, якщо він має дві пари
коренів у полі, які є протилежними
числами.Розкласти на незвідні у полі Р множники такі многочлени:

Знайти многочлен шостого степеня з кільця
 ,
якщо
,
якщо

Розкласти многочлен f(x) за степенями двочлена
 і знайти
і знайти
 ,
якщо:
,
якщо:
![]()
![]() належить
належить
![]() .
.
Знайти кратність кореня
 многочлена
:
многочлена
:

При яких значеннях
 многочлен
многочлен
 має
кратний корінь:
має
кратний корінь:

Визначити коефіцієнт
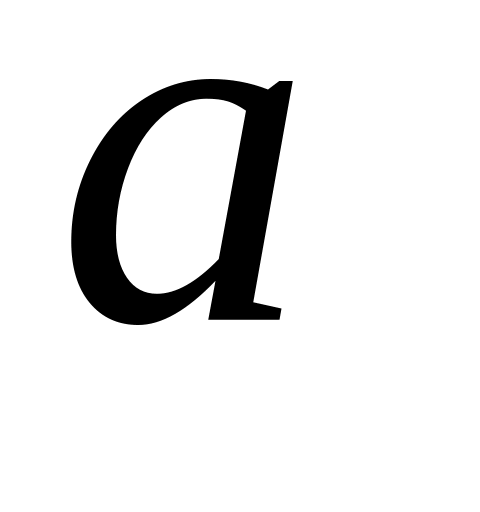 так,
щоб многочлен
так,
щоб многочлен
 мав число -1 коренем не нижче другої
кратності.
мав число -1 коренем не нижче другої
кратності.Відокремити кратні множники таких многочленів:

Визначити коефіцієнт так, щоб один з коренів многочлена
 був рівним подвійному другому.
був рівним подвійному другому.
Знайти многочлен третього степеня, якщо його корені рівні
 ,
де
,
де
 - корені многочлена
- корені многочлена
 .
.
§ 4. Раціональні дроби. Елементарні дроби. Розклад дробу на елементарні дроби над полями q,r і c Питання для самоконтролю:
Який раціональний дріб називається правильним?
Елементарний дріб у полі - це …
Чи є елементарний дріб правильним?
Чи вірно, що
 ,
якщо
,
якщо
 і
і
 - взаємно прості многочлени? Відповідь
пояснити.
- взаємно прості многочлени? Відповідь
пояснити.Як можна представити правильний дріб
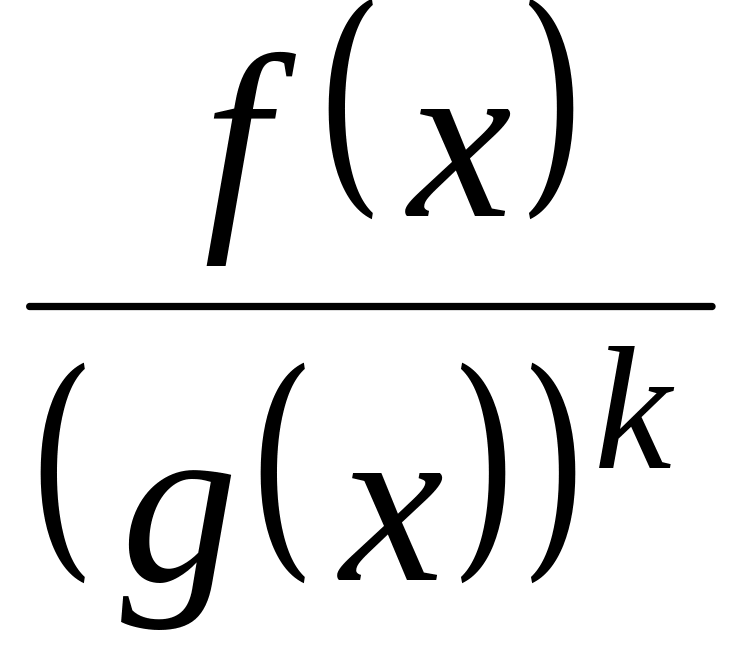 ,
,
де - многочлен незвідний над полем ?
Чи єдиний розклад правильного дробу
 на елементарні дроби у даному полі.
Відповідь пояснити
на елементарні дроби у даному полі.
Відповідь пояснити
Задачі
Довести тотожність:

Використовуючи інтерполяційну формулу Ньютона, побудувати многочлен найменшого степеня
 за такою таблицею:
за такою таблицею:
|
-3 |
-2 |
-1 |
|
|
|
1 |
2 |
4 |
|
|
|
-1 |
0 |
1 |
2 |
3 |
|
6 |
5 |
0 |
3 |
2 |
Знайти многочлен найменшого степеня за такою таблицею:
|
1 |
і |
-1 |
-і |
|
і |
1 |
-і |
-1 |
Обчислити
![]()
|
1 |
2 |
3 |
4 |
|
1 |
|
|
|
Знайти цілі числа
 такі, що
такі, що
а)
 ;
;
б)
 .
.
5) У полі
![]() знайти нескоротний дріб, який дорівнює
знайти нескоротний дріб, який дорівнює
![]() ,
,
![]() .
.
6) Перевірити,
чи є раціональні дроби
елементарними над полем
,
якщо:

7) Розкласти
дріб на елементарні дроби:
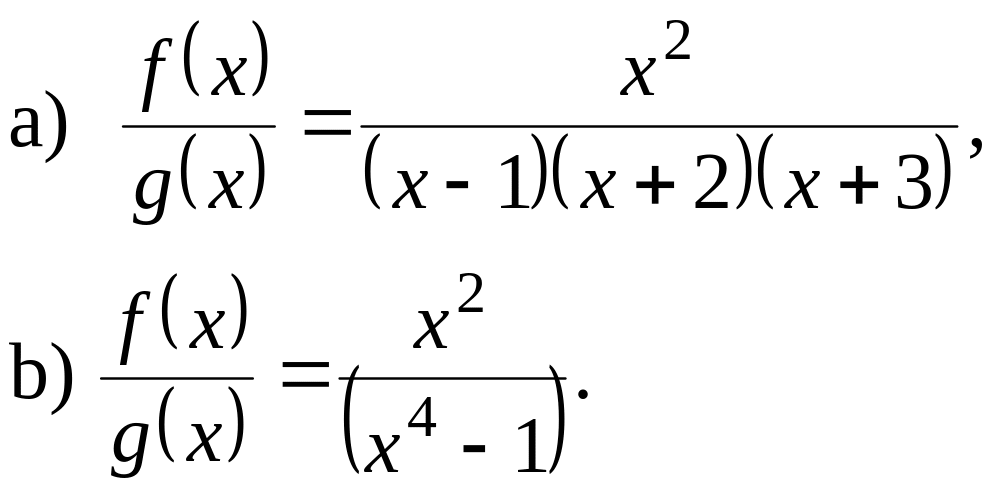
8) Розкласти
дріб на елементарні дроби:
![]()
9) Розкласти
дріб на елементарні дроби в полі
комплексних чисел:
![]()
10) Розкласти
дріб на елементарні дроби в полі
раціональних чисел:
![]()
