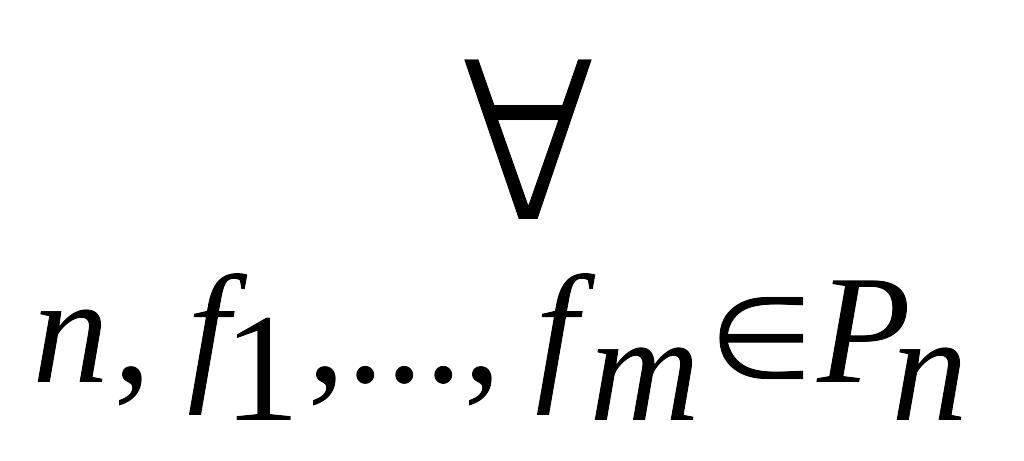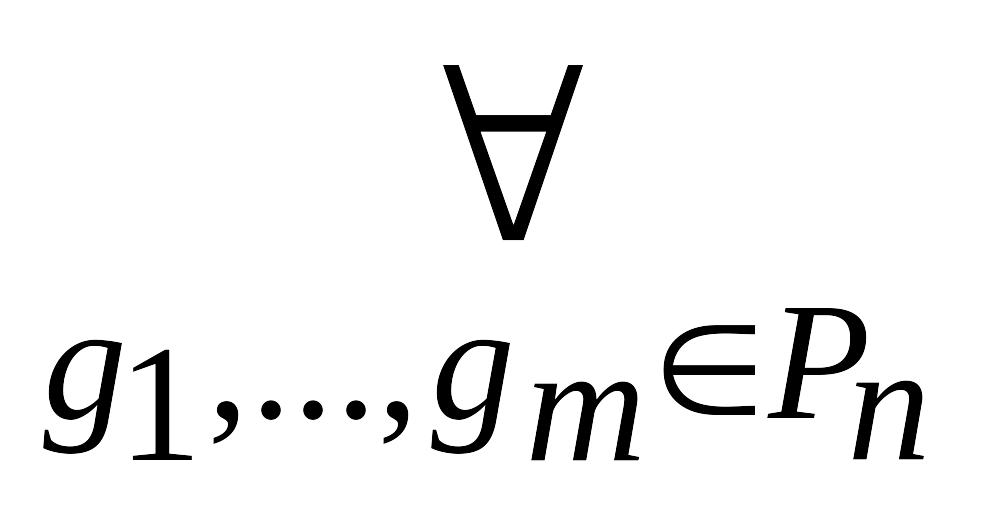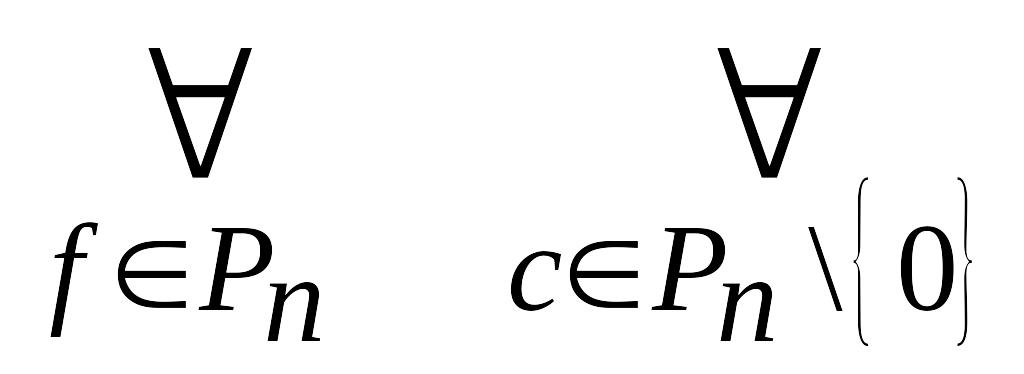- •Розділ I. Многочлени від однієї змінної § 1. Кільце многочленів. Алгебраїчна і функціональна рівність многочленів. Відношення подільності в кільці многочленів. Ділення з остачею.
- •Відношення подільності многочленів над полем р має такі властивості:
- •Приклади розв’язування задач.
- •§ 2. Ділення многочлена на двочлен ( X- ). Теорема Безу. Схема Горнера. Розклад многочлена за степенями ( X-). Найбільший спільний дільник і найменше спільне кратне многочленів. Алгоритм Евкліда.
- •Метод невизначених коефіцієнтів :
- •Властивості взаємно простих многочленів:
- •Алгоритм Евкліда.
- •Властивості нсд:
- •Приклади розв’язування задач.
- •§ 3. Незвідні многочлени над полем. Розклад многочленів на незвідні множники. Похідна многочлена. Кратні корені.
- •Властивості незвідних многочленів над полем :
- •Виконуються такі рівності:
- •Відокремлення кратних множників.
- •Приклади розв’язування задач.
- •§ 4. Раціональні дроби. Елементарні дроби. Розклад дробу на елементарні дроби надполями q,r і c.
- •Приклади розв’язування задач.
- •Розділ II. Многочлени від кількох змінних § 5. Кільце многочленів від n змінних. Розклад многочлена на добуток незвідних множників. Симетричні многочлени.
- •Властивості подільності:
- •Властивості незвідних многочленів:
- •Властивості симетричних многочленів:
- •Елементарні симетричні многочлени:
- •Представлення симетричних сум через елементарні симетричні многочлени:
- •Приклади розв’язування задач.
- •§ 6. Застосування симетричних многочленів до розвязування деяких задач з елементарної алгебри. Приклади розв’язування задач.
- •§ 7. Дискримінант та результант двох многочленів, їх властивості і застосування до розв'язування задач.
- •Властивості результанта:
- •Приклади розв’язування задач.
- •Розділ III.Многочлени над полем комплексних чисел і над полем дійсних чисел § 8. Многочлени над полем комплексних чисел. Алгебраїчна замкненість поля комплексних чисел.
- •Приклади розв’язування задач.
- •§ 9. Многочлени над полем дійсних чисел.
- •Приклади розв’язування задач.
- •§ 10. Рівняння третього степеня.
- •Якщо коефіцієнти p I q рівняння (1) є дійсними числами, то:
- •Приклади розв’язування задач.
- •§ 11. Відокремлення дійсних коренів многочленів. Теорема Штурма.
- •Властивості ряду Штурма:
- •Застосування теореми Штурма:
- •Приклади розв’язування задач.
- •Розділ IV. Многочлени над полем раціональних чисел та алгебраїчні числа § 12. Цілі і раціональні корені многочлена з цілими коефіцієнтами. Критерій незвідності Ейзенштейна.
- •Приклади розв’язування задач.
- •§ 13. Алгебраїчні і трансцендентні числа. Будова простого алгебраїчного розширення поля.
- •Приклади розв’язування задач.
- •§ 14. Позбавлення від алгебраїчної ірраціональності в знаменнику дробу.
- •Приклади розв’язування задач.
- •Розділ V. Цікаві задачки § 15. Задачі на доведення
- •§ 16. Нестандартні задачі
- •§ 17. Задачі для самостійного розв’язання
- •Словничок термінів
- •Список використаних джерел.
Розділ II. Многочлени від кількох змінних § 5. Кільце многочленів від n змінних. Розклад многочлена на добуток незвідних множників. Симетричні многочлени.
Означення
1. Кільцем
многочленів
![]() від
змінних
від
змінних
![]() над областю цілісності R
називається кільце многочленів від
однієї змінної
над областю цілісності R
називається кільце многочленів від
однієї змінної
![]() над кільцем
над кільцем
![]() ,
тобто
=
[
].
,
тобто
=
[
].
Кільце
многочленів
![]() над областю цілісності R
є область цілісності, причому кожен
елемент
над областю цілісності R
є область цілісності, причому кожен
елемент
![]() можна подати як скінчену суму:
можна подати як скінчену суму:
![]() ,
(1),
,
(1),
де
![]()
Означення
2. Кожний
елемент кільця
називається многочленом
від
змінних над
і позначається
![]() ,
,
![]()
і т.д.
Кожен
доданок
![]() в сумі (1) називається членом
многочлена
в сумі (1) називається членом
многочлена
![]() ,
елемент
,
елемент
![]() – коефіцієнтом
цього члена. Два члени, які відрізняються
тільки коефіцієнтами називаються
подібними.
– коефіцієнтом
цього члена. Два члени, які відрізняються
тільки коефіцієнтами називаються
подібними.
Приклад:
![]() -
многочлен
від двох змінних
x,
y.
-
многочлен
від двох змінних
x,
y.
Теорема
1. Будь-який
многочлен
![]() можна подати у канонічній формі ( без
подібних членів ).
можна подати у канонічній формі ( без
подібних членів ).
Означення
2 Степенем
члена
![]() многочлена називається сума
многочлена називається сума
![]() .
Число
.
Число
![]() називається степенем
даного члена відносно
називається степенем
даного члена відносно
![]() .
Найбільший із степенів членів називається
степенем
многочлена,
а член з найбільшим степенем – старшим
членом многочлена.
.
Найбільший із степенів членів називається
степенем
многочлена,
а член з найбільшим степенем – старшим
членом многочлена.
Приклад:
![]()
7
– степінь многочлена,
![]() -
старший член многочлена.
-
старший член многочлена.
Означення 3. Якщо всі члени многочлена мають однаковий степінь, то многочлен називається однорідним.
Теорема
2. Якщо
і
– відмінні від нуля многочлени з
,
де
– область цілісності, то
![]() .
.
Нехай
і
![]() - два члени многочлена
.
Вважається, що перший елемент вищий від
другого, якщо
- два члени многочлена
.
Вважається, що перший елемент вищий від
другого, якщо
![]() .
Відношення “бути
вищим”
на множині членів многочленів є лінійним
строгим порядком, його називають
лексикографічним
(позначають
.
Відношення “бути
вищим”
на множині членів многочленів є лінійним
строгим порядком, його називають
лексикографічним
(позначають
![]() ).
).
Приклад:
![]() -
лексикографічний запис
многочлена,
-
лексикографічний запис
многочлена,
![]() - вищий член.
- вищий член.
Лема 1. Вищий член добутку двох многочленів дорівнює добутку вищих членів цих многочленів.
Означення
4.
Вважатимемо, що многочлен
![]() ділиться на многочлен
ділиться на многочлен
![]() і записуватимемо
і записуватимемо
![]() ,
якщо існує такий многочлен
,
якщо існує такий многочлен
![]() ,
що
,
що
![]() .
При цьому
- дільник
.
.
При цьому
- дільник
.
Властивості подільності:
Означення
5.
Многочлен
![]() називається незвідним
у
полі Р,
якщо
називається незвідним
у
полі Р,
якщо
![]() і
і
![]() .
.
Многочлен
![]() називається звідним
у полі Р,
якщо
називається звідним
у полі Р,
якщо
![]() і
і
![]() .
.
Властивості незвідних многочленів:
Якщо р незвідний у полі многочлен, то і будь-який асоційований з ним многочлен
 незвідний у полі
.
незвідний у полі
.Якщо
 і
і
 незвідні у полі Р многочлени і
незвідні у полі Р многочлени і
 , то
і
асоційовані.
, то
і
асоційовані.Будь-який многочлен
 першого степеня незвідний у полі
.
першого степеня незвідний у полі
.
Теорема
3.
Будь-який многочлен
![]() над полем Р ненульового степеня множна
подати як добуток многочленів, незвідних
у полі Р, причому єдиним способом з
точністю до сталих множників і їх
порядку.
над полем Р ненульового степеня множна
подати як добуток многочленів, незвідних
у полі Р, причому єдиним способом з
точністю до сталих множників і їх
порядку.
Лема
2. Для
будь-якої скінченої системи елементів
![]() (
(![]() –
область цілісності), відмінних від нуля,
існує єдиний ( з точністю до дільників
одиниці ) НСД.
–
область цілісності), відмінних від нуля,
існує єдиний ( з точністю до дільників
одиниці ) НСД.
Означення
6. Многочлен
![]() називається примітивним
(відносно
),
якщо НСД його коефіцієнтів дорівнює
одиниці.
називається примітивним
(відносно
),
якщо НСД його коефіцієнтів дорівнює
одиниці.
Лема
3. Добуток
двох примітивних многочленів з
![]() є примітивний многочлен.
є примітивний многочлен.
Означення
7. Многочлен
![]() називається симетричним
відносно змінних
називається симетричним
відносно змінних
![]() ,
якщо внаслідок довільної перестановки
змінних
утворюється многочлен рівний даному.
,
якщо внаслідок довільної перестановки
змінних
утворюється многочлен рівний даному.
Приклад:![]() симетричний
відносно
симетричний
відносно
![]() ;
;
![]() симетричний
відносно
симетричний
відносно
![]() ,
але несиметричний відносно
,
але несиметричний відносно
![]() або
або
![]() не симетричний відносно
не симетричний відносно
![]()