§ 14. Позбавлення від алгебраїчної ірраціональності в знаменнику дробу.

Основні методи розв’язування задач на позбавлення від ірраціональності в знаменнику дробу ґрунтуються на таких фактах :

1. Якщо - многочлен від однієї змінної над полем з коренями (які можуть і не належати ), то будь-який симетричний многочлен над полем при набуває значення, яке є елементом поля .

2. Поле , утворене з числового поля приєднанням кореня α, незвідного у полі многочлена -го степеня , складається з усіх чисел виду , де - довільні числа з поля .

Крім цього, використовуються формули скороченого множення:

Нехай дано дріб , де і - многочлени над полем Q,

а α - ірраціональний корінь незвідного многочлена з раціональними коефіцієнтами ( 0). Слід виконати тотожні перетворення даного дробу, щоб позбутись ірраціональності в знаменнику. Якщо , то ділячи на з остачею, отримаємо рівність .

Підставляючи значення дістанемо , тому ,

де . Отже завжди можна вважати степінь знаменника даного дробу меншим за . Але тоді зрозуміло, що , бо - незвідний.

Нехай тепер і – такі многочлени над Q, що

(1)

Тоді і (2)

Таким чином, щоб знищити ірраціональність у знаменнику дробу , де α - корінь незвідного многочлена , потрібно виконати такі дії :

1) якщо , то замінити на , де - остача від ділення на ;

2) знайти многочлени і , які задовольняють рівність (1) ;

3) обчислити і подати дріб за формулою (2).

Приклади розв’язування задач.

14.1. Позбавитися від ірраціональності в знаменнику дробу де .

Розв’язання.

Нехай , а - мінімальний многочлен . Розділимо на “кутом”:

- _ х⁴ - 4х - 2 | x² + 1 -

x⁴ + x² | x² - 1 -

_ - x² - 4x - 2

- x² - 1

-4x - 1 -

Маємо .

Ділимо на :

- _ х² + 1 |-4x – 1 -

х² +¼ х |-¼ x + 1/16 -

_ -¼ x + 1

-¼ x – 1/16

17/16 -

Отже ( , ) = 1 – взаємно прості і = + . Тоді

14.2. Позбавитися від ірраціональності в знаменнику дробу .

Розв’язання.

Заданий дріб є значенням раціонального дробу при , яке є незвідним у полі Q многочлена . Многочлени взаємно прості. Знайдемо лінійне представлення їхнього найбільшого дільника. Ділення многочленів виконаємо ”кутом” :

_ х³ – 2 |3x² + x + 1

х³ + 1/3х²+ 1/3х | 1/3x – 1/9

_ - 1/3х² – 1/3х – 2

- 1/3х² – 1/9х – 1/9

- 2/9х – 17/9

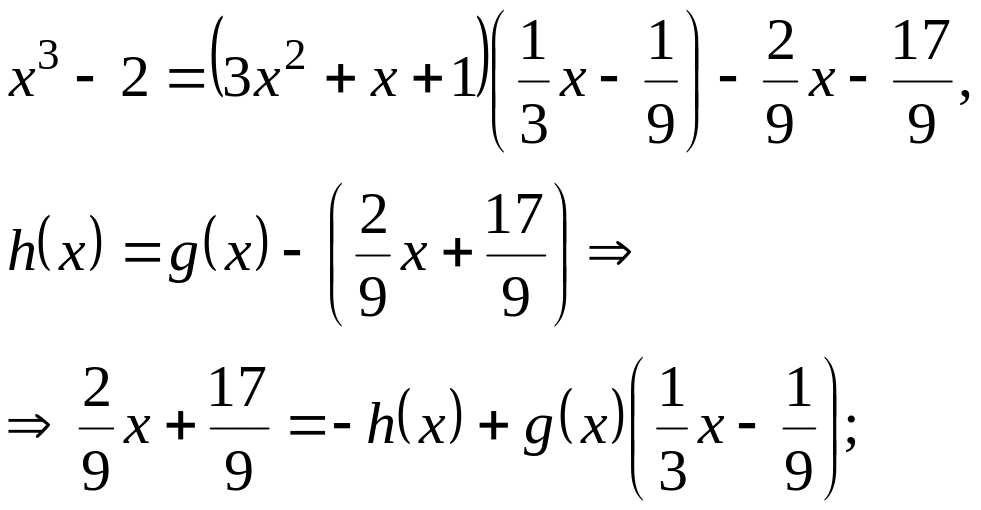
Тодi

_ 3x² + x + 1 |-2/9x – 17/9

3x² + 51/2x |-27/2x + 441/4

_ - 49/2x + 1

- 49/2x - 833/4

837/4

Звідси

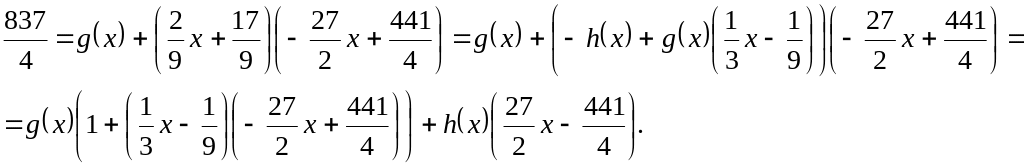
Оскільки , то

14.3. Позбавитися від ірраціональності в знаменнику дробу .

Розв’язання.

Застосуємо формулу скороченого множення : Тоді маємо:

14.4. Позбавитися від ірраціональності в знаменнику дробу

Розв’язання.

I спосіб.

Введемо позначення . Тоді дріб набуває вигляду , де

- елементарний многочлен від трьох змінних. Складемо вираз із степеневих сум з парними індексами так, щоб у ньому множником був многочлен :

, тоді

Звідси .

Враховуючи, що ,

маємо

.

II спосіб.

Домножимо даний дріб на спряжне і виконаємо ряд перетворень, використовуючи формулу скороченого множення: