§ 9. Многочлени над полем дійсних чисел.

Нехай (1) - многочлен з дійсними коефіцієнтами.

Теорема 1. Якщо комплексне число - є коренем многочлена (1), то спряжене комплексне число є коренем цього ж многочлена.

Теорема 2. Якщо комплексне число - є коренем -ї кратності многочлена з дійсними коефіцієнтами (1), то спряжене комплексне число є коренем многочлена тієї ж кратності.

Теорема 3. Кожний многочлен над полем , степінь якого перевищує 2, є звідним у цьому полі.

Теорема 4. Кожний многочлен над полем дійсних чисел допускає єдиний розклад на незвідні множники (лінійні і квадратні тричлени) в цьому полі виду :

Приклади розв’язування задач.

9.1. Розв’язати рівняння , якщо .

Розв’язання.

Задане рівняння має дійсні коефіцієнти, тому число теж є коренем, а многочлен ділиться на :

(наслідок з теореми Безу). Виконаємо ділення ”кутом”:

x⁴ - x³ - 11x² + 31x - 20 | x² - 4x + 5

x⁴ - 4x³ + 5x² | x² + 3x - 4

3x³ - 16x² + 31x

3x³ - 12x² + 15x

_-4x² + 16x - 20

-4x² + 16x - 20

0

Щоб знайти інші корені заданого рівняння розв’яжемо рівняння .

Корені: .Тому

9.2. Число є коренем рівняння з дійсними коефіцієнтами . Знайти та два інші корені.

Розв’язання.

Маємо , а тому - теж корінь (див. вище).Тоді многочлен поділимо на : .

x³ + x² + ax + b | x² + 6x + 10

x³ + 6x² + 10x | x - 5

-5x² + (a - 10)x + b

-5x² - 30x - 50

(a + 20)x + (b + 50) =

Щоб необхідно і достатньо, щоб :

, 0 тому .

Тоді

§ 10. Рівняння третього степеня.

Нехай - рівняння третього степеня з комплексними коефіцієнтами. За допомогою підстановки зведемо його до виду (1)

Число називають дискримінантом рівняння (1). Корені цього рівняння знаходять за формулою , яка називається формулою Кардано.

Якщо і є тими значеннями кубічних коренів, при яких є коренями рівняння (1), то решту коренів цього рівняння обчислюють так:

Числа знаходяться з умови .

Якщо коефіцієнти p I q рівняння (1) є дійсними числами, то:

1. при рівняння має один дійсний корінь і два комплексних спряжених корені;

2. при рівняння має три дійсних корені і два з яких дорівнюють один одному;

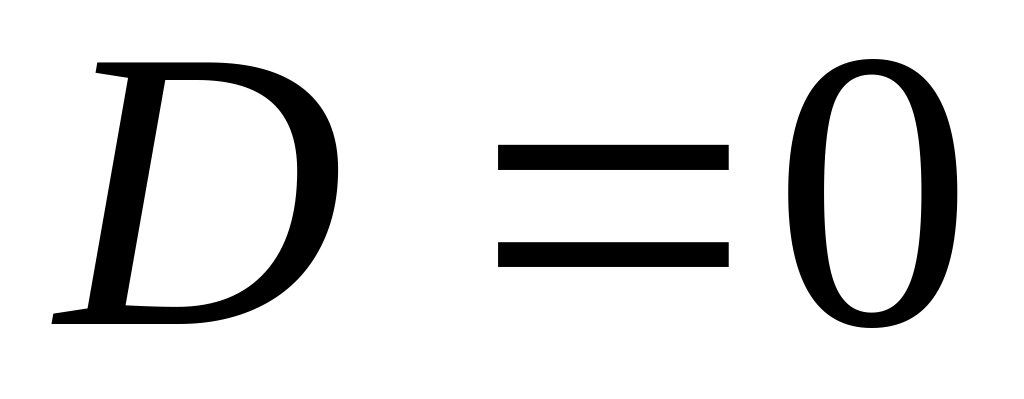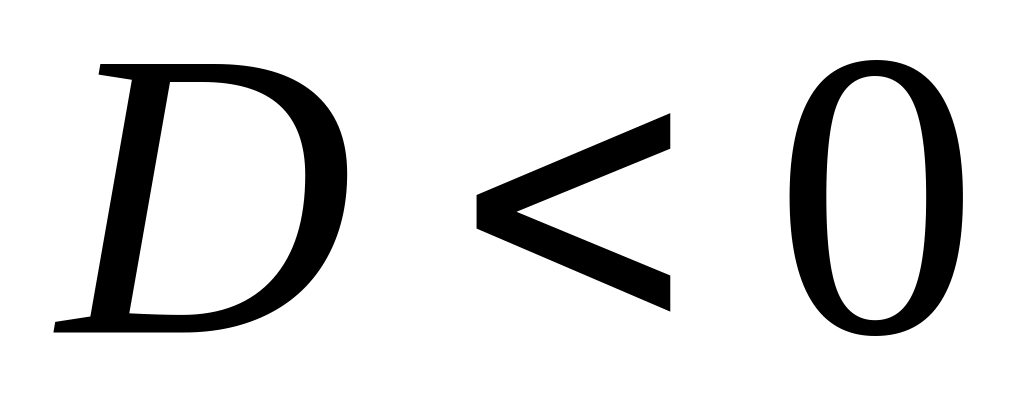3. при рівняння має три дійсних різних корені.

Приклади розв’язування задач.

10.1. При яких дійсних значеннях рівняння має один дійсний корінь і два комплексних корені.

Розв’язання.

Щоб рівняння мало один дійсний корінь і два комплексних корені треба, щоб . Тому

Тому такі корені будуть при

10.2. Довести, що корені рівняння є дійсними при будь-якому дійсному значенню числа .

Розв’язання.

Зведемо це рівняння до виду (1), ввівши заміну : . Матимемо

Щоб корені рівняння були дійсними при будь-якому дійсному значенню числа треба, щоб виконувалася умова, що .

Дискримінант цього рівняння:

< 0.

Як бачимо умова виконується.

Отже рівняння має три різних дійсних корені при будь-якому дійсному значенню числа , що і треба було довести.

10.3. Розв’язати рівняння:

Розв’язання.

Дане рівняння є рівнянням виду (1), тому обчислюємо його дискримінант:

.

Тоді

Далі

10.4. Розв’язати рівняння:

Розв’язання.

Зведемо це рівняння до рівнянням виду (1), помноживши спершу обидві його частини на :

Виконажмо заміну:

Маємо:

Знаходимо дискримінант:

Тоді