
- •Розділ I. Многочлени від однієї змінної § 1. Кільце многочленів. Алгебраїчна і функціональна рівність многочленів. Відношення подільності в кільці многочленів. Ділення з остачею.
- •Відношення подільності многочленів над полем р має такі властивості:
- •Приклади розв’язування задач.
- •§ 2. Ділення многочлена на двочлен ( X- ). Теорема Безу. Схема Горнера. Розклад многочлена за степенями ( X-). Найбільший спільний дільник і найменше спільне кратне многочленів. Алгоритм Евкліда.
- •Метод невизначених коефіцієнтів :
- •Властивості взаємно простих многочленів:
- •Алгоритм Евкліда.
- •Властивості нсд:
- •Приклади розв’язування задач.
- •§ 3. Незвідні многочлени над полем. Розклад многочленів на незвідні множники. Похідна многочлена. Кратні корені.
- •Властивості незвідних многочленів над полем :
- •Виконуються такі рівності:
- •Відокремлення кратних множників.
- •Приклади розв’язування задач.
- •§ 4. Раціональні дроби. Елементарні дроби. Розклад дробу на елементарні дроби надполями q,r і c.
- •Приклади розв’язування задач.
- •Розділ II. Многочлени від кількох змінних § 5. Кільце многочленів від n змінних. Розклад многочлена на добуток незвідних множників. Симетричні многочлени.
- •Властивості подільності:
- •Властивості незвідних многочленів:
- •Властивості симетричних многочленів:
- •Елементарні симетричні многочлени:
- •Представлення симетричних сум через елементарні симетричні многочлени:
- •Приклади розв’язування задач.
- •§ 6. Застосування симетричних многочленів до розвязування деяких задач з елементарної алгебри. Приклади розв’язування задач.
- •§ 7. Дискримінант та результант двох многочленів, їх властивості і застосування до розв'язування задач.
- •Властивості результанта:
- •Приклади розв’язування задач.
- •Розділ III.Многочлени над полем комплексних чисел і над полем дійсних чисел § 8. Многочлени над полем комплексних чисел. Алгебраїчна замкненість поля комплексних чисел.
- •Приклади розв’язування задач.
- •§ 9. Многочлени над полем дійсних чисел.
- •Приклади розв’язування задач.
- •§ 10. Рівняння третього степеня.
- •Якщо коефіцієнти p I q рівняння (1) є дійсними числами, то:
- •Приклади розв’язування задач.
- •§ 11. Відокремлення дійсних коренів многочленів. Теорема Штурма.
- •Властивості ряду Штурма:
- •Застосування теореми Штурма:
- •Приклади розв’язування задач.
- •Розділ IV. Многочлени над полем раціональних чисел та алгебраїчні числа § 12. Цілі і раціональні корені многочлена з цілими коефіцієнтами. Критерій незвідності Ейзенштейна.
- •Приклади розв’язування задач.
- •§ 13. Алгебраїчні і трансцендентні числа. Будова простого алгебраїчного розширення поля.
- •Приклади розв’язування задач.
- •§ 14. Позбавлення від алгебраїчної ірраціональності в знаменнику дробу.
- •Приклади розв’язування задач.
- •Розділ V. Цікаві задачки § 15. Задачі на доведення
- •§ 16. Нестандартні задачі
- •§ 17. Задачі для самостійного розв’язання
- •Словничок термінів
- •Список використаних джерел.
Розділ III.Многочлени над полем комплексних чисел і над полем дійсних чисел § 8. Многочлени над полем комплексних чисел. Алгебраїчна замкненість поля комплексних чисел.
Нехай
- деякий многочлен над полем
.
Якщо
![]() ,
то існує розширення
,
то існує розширення
![]() поля
,
в якому міститься деякий корінь многочлена
.З
цього твердження випливає, що для
будь-якого многочлена
поля
,
в якому міститься деякий корінь многочлена
.З
цього твердження випливає, що для
будь-якого многочлена
![]() степеня
існує таке розширення
степеня
існує таке розширення
![]() поля
,
що
можна подати в
поля
,
що
можна подати в
![]() у вигляді добутку лінійних множників.
у вигляді добутку лінійних множників.
Поле
![]() називається полем
розкладу многочлена
,
якщо
розкладається в
називається полем
розкладу многочлена
,
якщо
розкладається в
![]() на лінійні множники. Поле
,
яке є полем розкладу будь-якого многочлена
,
називається алгебраїчно
замкненим.
на лінійні множники. Поле
,
яке є полем розкладу будь-якого многочлена
,
називається алгебраїчно
замкненим.
Теорема 1. Многочлен непарного степеня над полем дійсних чисел має принаймні один дійсний корінь.
Теорема
2.
Кожний многочлен степеня
![]() з дійсними коефіцієнтами має принаймні
один комплексний корінь.
з дійсними коефіцієнтами має принаймні
один комплексний корінь.
Теорема 3. (Основна теорема теорії многочленів):
Довільний
многочлен ненульового степеня з
комплексними коефіцієнтами
![]() має хоча б один комплексний корінь.
має хоча б один комплексний корінь.
Теорема 4. Кожний многочлен, степінь якого вища за одиницю, звідний у полі комплексних чисел.
Наслідок. Для того, щоб многочлен був незвідним у полі комплексних чисел, необхідно і достатньо, щоб його степінь дорівнював 1.
Теорема 5. Кожний многочлен -го степеня у полі комплексних чисел єдиним чином (з точністю до порядку множників) розкладається на лінійні множники у цьому полі:
![]() ,
,
де
![]() - корені,
- корені,
![]() - старший коефіцієнт
.
- старший коефіцієнт
.
Терема 6. Многочлен -го степеня у полі комплексних чисел має точно коренів.
Очевидно,
що всі корені многочлена
![]() над полем комплексних чисел належать
цьому ж полю, тобто полем розкладу
будь-якого многочлена
з комплексними коефіцієнтами є поле С
(поле комплексних чисел ). Тому поле
комплексних чисел є алгебраїчно замкненим
і для коренів многочлена
у полі С є справедливими формули Вієта:
над полем комплексних чисел належать
цьому ж полю, тобто полем розкладу
будь-якого многочлена
з комплексними коефіцієнтами є поле С
(поле комплексних чисел ). Тому поле
комплексних чисел є алгебраїчно замкненим
і для коренів многочлена
у полі С є справедливими формули Вієта:
![]()
![]()
..........................................
![]()
Приклади розв’язування задач.
8.1.
Знайти
многочлен найменшого степеня, в якого
число 2 - подвійний корінь, а
![]() – прості.
– прості.
Розв’язання.
Могочлен , виходячи з умови, можна розкласти на незвідні множники:
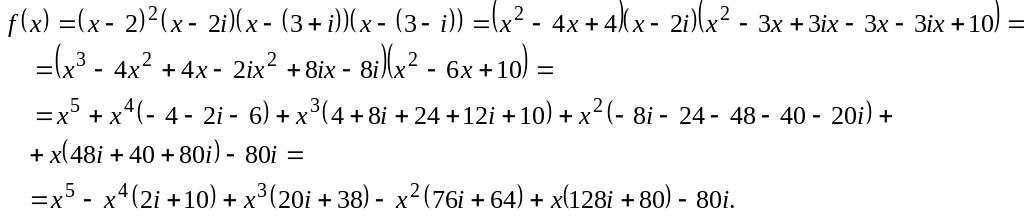
8.2.
Знайти
суму кубів коренів многочлена
![]()
Розв’язання.
Нехай – корені многочлена . За теоремою Вієта маємо систему:
![]()
![]()
8.3.
Знайти
зведені многочлени, в яких корені
задовольняють умову:
![]() ,
а
,
а
![]() є коренями многочлена
є коренями многочлена
![]() .
.
Розв’язання.
Запишемо
многочлен
![]()
![]() .
.
За
теоремою Вієта при умові, що
![]() - корені
,
маємо:
- корені
,
маємо:
![]()
Отримаємо
:
![]()
8.4.
Розкласти
на незвідні множники многочлен
![]() .
.
Розв’язання.
Знайдемо
корені многочлена
![]() .
.


Тоді
маємо, що
![]()
8.5.
Знайти суму кубів коренів многочлена
![]()
Розв’язання.
За
теоремою Вієта маємо:
![]()
Тоді

8.6.
Корені многочлена
утворюють арифметичну прогресію. Знайти
цей многочлен і його корені, якщо
![]()
Розв’язання.
Нехай
![]() -корені
многочлена
.
Так як вони утворюють арифметичну
прогресію, то виконується така умова:
-корені
многочлена
.
Так як вони утворюють арифметичну
прогресію, то виконується така умова:![]()
За
теоремою Вієта маємо:
![]()
Складемо
систему:
![]()
Розвязавши
її отримаємо такі значення:
![]()
Отже,
![]()
