Упражнения

1. Найдите законы распределения составляющих дискретной двумер­ной случайной величины, заданной законом распределения в виде таблицы

Y X	y1	y2
x1 x2 x3	0,12 0,18 0,10	0,10 0,11 0,39

X	x1	x2	x3	Y	y1	y2
p	0,22	0,29	0,49	p	0,40	0,60

2. Найдите вероятность того, что составляющая X двумерной слу­чайной величины примет значение X < и при этом составляющая Y примет значение Y< , если функция распределения величины (X, Y)

F(х,у) =

3. Найдите вероятность попадания случайно поставленной точки (X, У) в прямоугольник, ограниченный прямыми x= 0, x= , , , если функция распределения двумерной случайной величины F(х, у)=sinxsiny

4. Найдите плотность вероятности f(х, у) двумерной случайной ве­личины по известной функции распределения F(х, у)= ,

5. Плотность вероятности двумерной случайной величины определяет­ся выражением

Найдите коэффициент а.

6. Плотность вероятности двумерной случайной величины определя­ется выражением

Определите величину С и найдите функцию распределения F(х, у).

7. Плотность вероятности двумерной случайной величины определя­ется выражением

Найдите плотности распределения составляющих.

X Y	y1	y2
x1 x2 x3	0,15 0,30 0,35	0,05 0,12 0,03

8. Дискретная двумерная случайная величина задана таблицей

Найдите: а) условный закон распределения составляющей X при усло­вии, что составляющая Y приняла значение у₁; б) условный закон распре­деления составляющей Y при условии, что составляющая X приняла зна­чение x₂.

9. В условиях, изложенных в упражнении 7, найдите условные законы распределения вероятностей составляющих.

10. Плотность распределения непрерывной двумерной случайной вели­чины (X, У) задана выражением

Докажите, что составляющие X и Y независимы.

11. Дана таблица, определяющая закон распределения двумерной дис­кретной случайной величины

X Y	20	40	60
10			0
20
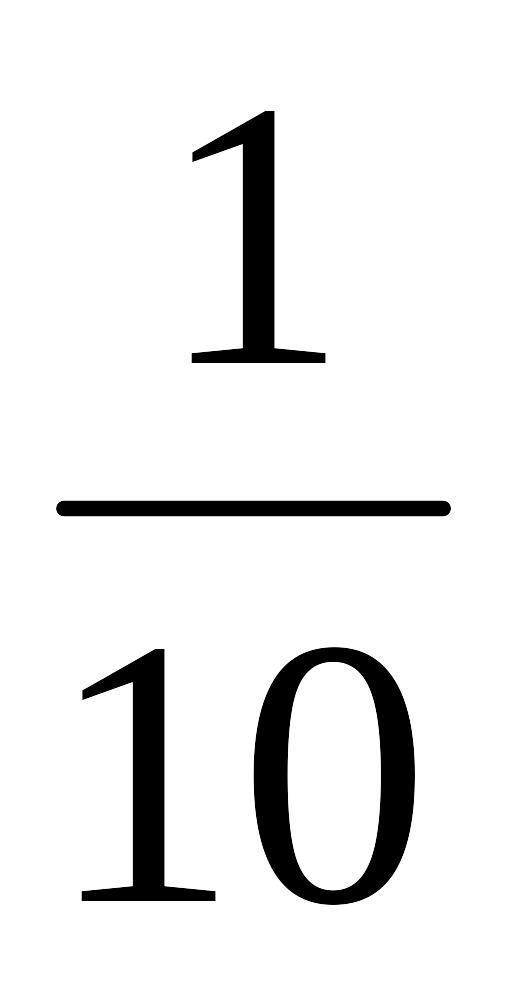
30

Найдите коэффициент корреляции . [ = 0,56]

12. Задана плотность вероятности непрерывной двумерной случайной величины

Найдите корреляционный момент и коэффициент корреляции .