4. Понятие o моментах распределения.

О п р е д е л е н и е 1. Начальным моментом порядка k случайной величины X называется математическое ожидание случайной вели­чины Х^k, где k - натуральное число:

v_k = M(X^k).

Cледствие. Если возможные значения непрерывной случайной величины расположены на всей числовой оси, то справедливы следующие предельные соотношения:

F(- )= F(x)=0; F(+ )= F(x)=1

2. Дифференциальная функция распределения. Дифференциальной функцией распределения непрерывной случайной величины Х (или ее плотностью вероятности, или ее плотностью распределения) называется функция f(x), равная производной интегральной функции

f(x)=F’(x).

Так как F(x)-неубывающая функция, то f(x) 0.

Из равенства (2.9) с учетом неравенства F(x+ )-F(x) F’(x) , справедливо для малых , и свойства 5(п.1) имеем

P(x<X<x+ F

P(x<X<x+ )

(для малых , т.е. вероятность попадания случайной величины X в интервал (x; x+ при малых приближенно равна произведению ее плотности вероятности в точке x на длину этого интервала.

Имеет место и следующая теорема.

Теорема. Вероятность попадания непрерывной случайной величины Х в интервал (a;b) равна определенному интегралу от ее плотности вероятности, взятому в пределах от a до b:

P(a<X<b)= (2.13)

Доказательство. Так как F(x)является первообразной для f(x), то на основании формулы Ньютона-Лейбница имеем

(2.14)

Теперь с учетом (2.9), (2.12), (2.14) получим искомое равенство.

Из (2.13) следует, что геометрическая вероятность P(a<X<b) представляет собой площадь криволинейной трапеции, ограниченной графиком плотности вероятности y=f(x) и отрезками прямых y = 0, x = a и x = b.

Следствие. В частности, если f(x) - четная функция и концы интервала симметричны относительно начала координат, то

P(-a<X<a)=P( <a)=2 (2.15).

Действительно.

П р и м е р 1. Пусть задана плотность вероятности случайной величины X

Найдем вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу(0,5; 1).

Согласно формуле (2.13), искомая вероятность

P(0,5<X<1)=2 =0,75.

Заменяя в формуле (2.14) а на - и b на х, получим

F(x) - F(- = откуда в силу приведенного выше следствия (п.1)

F(x)=

Выражение (2.16)позволяет найти интегральную функцию распределения F(x) по ее плотности вероятности.

Заметим что формулы (2.16) и отмеченного следствия вытекает что

Пример 2. Пусть плотность вероятности случайной величины Х задана так:

f(x)= (-

Требуется найти коэффициент А, функцию распределения F(x)и вероятность попадания случайной величины Х в интервал (0; 1).

Покажем, что M(X)=a, или =D(x)Согласно формуле(2.18), получаем M(X)= dx.

Введя новую переменную t по формуле (2.24), с учетом равенства(2.25) получим M(X)= )e dt+ dt=a- e / =a.

Далее, а в соответствие с формулой (2.19)

D(X)= e- dx.

Воспользовавшись подстановкой(2.24), получим:

D(X)=

Применяя здесь метод интегрирования по частям (t=u, te dt=dv), получим с учетом (2.25)

D(X)=-

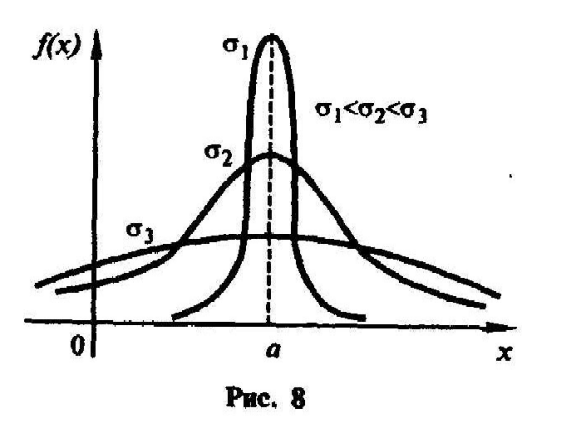
График функции (кривая Гаусса) имеет вид(рис 6). С учетом графика этой функции график функции (2.22) будет иметь вид (рис.7). Причем его максимальная ордината равна1/( ). Значит эта ордината убывает с возрастанием значения (кривая «растягивается» к оси Ох-рис.8) и возрастает (кривая «сжимается» в положительном направлении оси Оу). Изменение значение параметра а (при неизменном значении ) не влияет на форму кривой.

Нормальное распределение с параметрами а=0 и называется нормированным. Плотность вероятности в случае такого распределения оказывается равной

Вероятность попадания случайной величины, распределенной по нормальному закону, в заданный интервал.

Пусть случайная величина Х распределена по нормальному закону. Тогда вероятность того что, Х примет значение, принадлежащее интервалу ( ), согласно теореме из п.2

P( <X< =

Проведя в этом интеграле замену переменной , t= получим

P( <X< =

Учитывая, что функция является первообразной для, и используя формулу Ньютона-Лейбница, будем иметь . (2.26)

П р и м е р 1. Пусть случайная величина Х распределена по нормальному закону с параметрами a=30 и . Найдем вероятность того, что Х примет значение, принадлежащее интервалу (10; 50).

Пользуясь формулой (2.26), получим

P(10<X<50)=

По таблице приложения 3 находим . Отсюда искомая вероятность

P(10<X<50)=2 =0,9544.

Вычисление вероятности заданного отклонения.

Часто требуется определить вероятность того, что отклонение нормально распределенной случайной величины Х от ее математического ожидания по абсолютной величине меньше заданного положительного числа , т.е нужно найти P(

Используя формулу (2.26) и учитывая что функция нечетная, имеем

P( т.е

P(

П р и м е р 2. Пусть случайная величина Х распределена по нормальному закону с параметрами a=20 и и .Найдем P(

Используя выражения (2.27) имеем

P(

По таблице приложения 3 находим . Поэтому P( .

Правило трех сигм.

Полагая в выражении (2.27), получим P(

Но (см.таблицу приложения 3) и, значит, P( .

Формула (2.28) означает, что событие, состоящие в осуществлении неравенства имеет вероятность, близкую к единице, т.у, является почти достоверным. Эта формула выражает так называемое правило трех сигм : если случайная величина распределена по нормальному закону распределения, то модуль ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

В заключении заметим, что нормальное распределения вероятностей имеет в теории вероятностей больше значений. Нормальному закону подчиняется вероятность при стрельбе по цели, его используют в теории погрешностей физических измерений и т.п.