1.7 Интегрирование иррациональных выражений

I. Интегралы вида

сводятся к интегралам от рациональной функции с помощью подстановки , где k – наименьшее общее кратное чисел .

II. Интегралы вида

рационализируется подстановкой: , где k – наименьшее общее кратное чисел .

Пример 1.11 Найти .

Решение. Наименьшее общее кратное чисел 4 и 2 равно числу 4, поэтому делаем подстановку

, ,

откуда

.

Возвращаясь к переменной , получим

.

Ответ: .

1.8 Интегрирование выражений, содержащих тригонометрические функции

I. Интегралы вида

(1.9)

находят, применяя различные тригонометрические формулы в зависимости от значений m и n.

1) хотя бы одно из чисел m и n положительно и нечетно. Пусть , тогда интеграл (1.9) можно преобразовать следующим образом:

.

Аналогично поступают в случае .

2) оба числа m и n – четные и положительные (или нуль). В этом случае степени в подынтегральной функции понижают с помощью формул:

.

3) если . В этом случае подынтегральная функция записывается в виде дроби, в знаменателе которой выделяется множитель (или ). Выражение заменяем на и делаем замену .

Пример 1.12 Найти .

Решение. По условию одна из степеней нечетная, поэтому можно записать

.

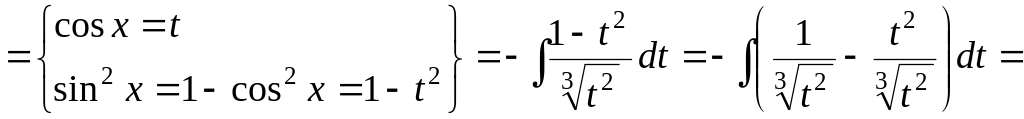
Ответ: .

Пример 1.13 Найти .

Решение. Для вычисления интеграла применим формулу понижения степени:

.

Ответ: .

Пример 1.14 Найти .

Решение. Здесь , поэтому полагаем:

, , .

Следовательно

.

Ответ: .

II. Интегралы вида

преобразуются с помощью тригонометрических формул

.

Пример 1.15 Найти .

Решение.

.

Ответ: .

III. В интегралах вида: (или ) где m – целое положительное число, применяется подстановка (или ).

Пример 1.16. Найти .

Решение. Сделаем подстановку , . Тогда

.

Ответ: .

1.9 Универсальная тригонометрическая подстановка

Интегралы вида где – рациональная функция, аргументами которой являются и , в общем случае приводятся к интегралам от рациональных функций с аргументом с помощью универсальной подстановки . При этом

; ; , .

Если подынтегральная функция является четной по обоим аргументам, то есть , то целесообразно использовать подстановку .

Пример 1.17 Найти .

Решение. Сделаем замену: . Тогда , , . Следовательно, получим

.

Ответ: .

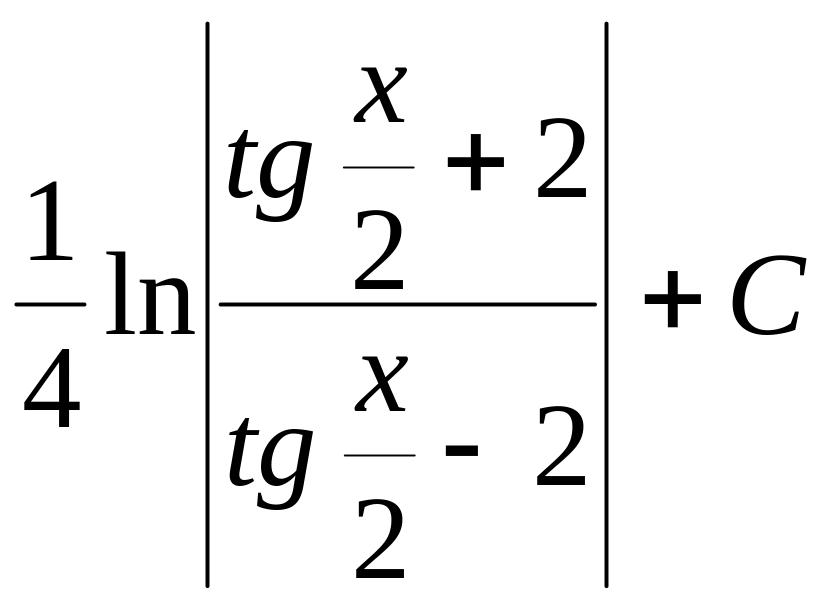2. Определенный интеграл

2.1 Понятие определенного интеграла

Пусть на отрезке задана функция . Разобьем этот отрезок произвольным образом точками на n частей длиной . Выберем внутри каждого отрезка точку .Найдем значение функции в точках .

Интегральной суммой функции на отрезке называется сумма вида:

. (2.1)

Определенным интегралом от функции на отрезке называется предел интегральной суммы (2.1), найденный при условии, что длина наибольшего из частичных отрезков стремится к нулю:

Некоторые свойства определенного интеграла:

1) , (2.2)

2) , (2.3)

3) , (2.4)

4) , (2.5)

5) Если , то , (2.6)

6) Если непрерывна и , то имеет место равенство:

, (2.7)

7) Если – какая-либо первообразная функции , то справедливо равенство:

. (2.8)

Формула (2.8) называется формулой Ньютона-Лейбница.

Пример 2.1 Вычислить определенный интеграл: .

Решение. По формуле (2.8)

.