1.4 Метод интегрирования по частям

Метод интегрирования по частям основан на применении формулы

, (1.7)

где – непрерывно дифференцируемые на некотором интервале функции.

К интегралам, которые находят методом интегрирования по частям, относятся интегралы следующих видов:

1) , где – полином n-ой степени от x.

В данном случае за следует выбрать , а за – или .

Таким образом, в результате применения формулы (1.7) мы пришли к интегралу более простому по отношению к исходному. Следует подчеркнуть, что формула интегрирования по частям может быть применена несколько раз, до тех пор, пока мы не придем к , т.е. не придем к интегралу .

2) , где – полином степени n от x.

В данном случае за обозначают , за . Формула интегрирования по частям применяется до тех пор, пока не останется .

3) .

В данном случае за следует выбирать ; ; , за . Тогда в результате применения формулы интегрирования по частям мы приходим к интегралам, содержащим только рациональные функции и радикалы.

4) Интегралы вида вычисляются с помощью двукратного применения формулы интегрирования по частям и последующего решения полученного уравнения относительно исходного интеграла. Следует отметить, что в данном случае безразлично, что изначально принимать за , а что за .

Пример 1.5 Найти .

Решение.

.

Пример 1.6 Найти .

Решение.

.

1.5 Интегрирование выражений, содержащих квадратный трехчлен

Интегралы вида и после выделения полного квадрата в квадратном трехчлене сводятся к одному из табличных интегралов вида VII, VIII, IX или X.

Пример 1.7 Найти .

Решение.

.

Ответ: .

Для вычисления интеграла вида необходимо выделить производную знаменателя в числителе подынтегральной функции:

, .

Тогда исходный интеграл преобразуется в сумму двух интегралов

.

Интеграл найдем методом занесения под знак дифференциала , интеграл сводится к табличным интегралам (предварительно выделяя полный квадрат в знаменателе).

Таким образом,

. (1.8)

Пример 1.8 Найти .

Решение. Найдем . Выделим в числителе функции: .

Таким образом

,

,

{табличный интеграл типа VII} .

Ответ: .

1.6. Интегрирование рациональных функций

Функция, заданная в виде

,

называется рациональной функцией.

Если , то дробь правильная, при – дробь неправильная.

Метод интегрирования правильной рациональной дроби состоит в разложении этой дроби на простейшие. При этом следует пользоваться следующим правилом:

а) если множитель входит в разложение только в первой степени, мы поставим ему в соответствие единственную простую дробь:

;

б) если в разложение входит множитель , то есть показатель степени , то ему соответствует сумма из простых дробей:

;

в) если в разложение входит множитель только в первой степени, то в соответствие ему ставится единственная простая дробь:

;

г) если в разложение входит множитель , показатель которого , то ему соответствует сумма из простых дробей

.

Итак, общее правило интегрирования рациональных дробей:

1. Если дробь неправильная, то представить её в виде суммы многочлена и правильной дроби.

2. Разложить знаменатель правильной рациональной дроби на множители.

3. Представить дробь в виде суммы простейших рациональных дробей.

4. Найти неизвестные коэффициенты способом сравнения соответствующих коэффициентов или способом частных значений (см. пример ниже).

5. Проинтегрировать многочлен и полученную сумму простейших дробей.

Пример 1.9 Разложить дробь на простейшие.

Решение. .

Найдём коэффициенты и .

1 способ – метод неопределённых коэффициентов:

.

Приравняем коэффициенты при и в обеих частях полученного равенства

.

2 способ – метод частных значений:

.

Ответ: .

Пример 1.10 Найти .

Решение. Подынтегральная функция есть неправильная рациональная дробь (степень числителя больше степени знаменателя), которую сначала представим в виде суммы многочлена и правильной рациональной дроби, разделив числитель и знаменатель по правилу «деления углом»:

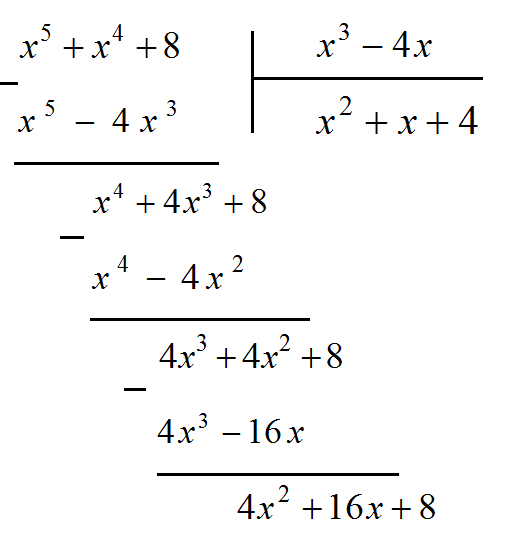
Следовательно,

.

Для представления правильной дроби в виде суммы простейших дробей преобразуем её знаменатель следующим образом:

.

Таким образом, полученную правильную дробь можно представить в виде суммы простейших дробей:

.

Отсюда получаем

.

Найдём коэффициенты , , методом частных значений. Подставляя поочерёдно значения , , , получаем

.

Итак,

.

Ответ: .