1. Неопределенный интеграл
1.1 Непосредственное интегрирование
Функция F(x) называется первообразной для функции f(x) на интервале (a;b), если
а) F(x) дифференцируема на (a;b),
б)
.
Если F(x)
является первообразной для функции
f(x)
на (a;b),
то и любая функция
,
также является первообразной для f(x)
на (a;b).
Неопределенным
интегралом от функции f(x)
на (a;b)
называется множество всех первообразных
функции f(x)
на этом интервале. Неопределенный
интеграл обозначается символом
.
Неопределенный интеграл записывают в
виде формулы:
,
(1.1)
где
– любая из первообразных для функции
f(x)
на (a;b),
С – произвольная постоянная.
Свойства неопределенного интеграла:
Таблица основных неопределенных интегралов:
.
.
.
.
.
.
.
.
.
.
.
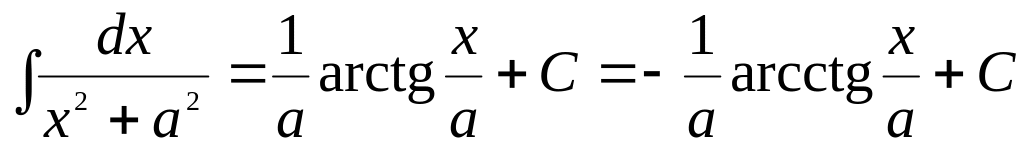Метод непосредственного интегрирования состоит в сведении заданного интеграла к сумме или разности табличных интегралов путем тождественных преобразований подынтегральной функции.
Пример 1.1 Найти
.
Решение. Преобразуем подынтегральное выражение:
.
Таким образом, получаем:
.
Ответ:
.
1.2 Метод занесения под знак дифференциала
Метод занесения под знак дифференциала основан на определении дифференциала функции одной переменной:
(1.2)
и
свойстве инвариантности дифференциала
первого порядка: если
,
то
.
(1.3)
В силу этого свойства, таблица интегралов оказывается справедливой, независимо от того, является ли переменная интегрирования независимой переменной или дифференцируемой функцией.
Пример 1.2 Найти
.
Решение. Применим метод занесения под знак дифференциала, воспользовавшись формулой (1.3):
Ответ:
.
1.3 Метод замены переменной в неопределенном интеграле
Метод замены
переменной заключается в том, что в
интеграле
,
нахождение которого затруднительно,
вводят новую переменную
.
При этом необходимо, чтобы полученный
интеграл
стал табличным или, по крайней мере, был
бы ясен способ его нахождения. После
вычисления
следует вернуться к исходной переменной.
Пример 1.3 Найти
.
Решение.
Подстановкой
знаменатель упрощается, и интеграл
приводится к табличным интегралам:
.
Ответ:
.
Тригонометрические и гиперболические подстановки
Часто для вычисления
интегралов, содержащих радикалы вида
применяются тригонометрические и
гиперболические подстановки.
Если интеграл содержит
,
то используем следующую замену:
(1.4)
Пример 1.4 Найти
.
Решение. После применения тригонометрической подстановки получим
.
Для вычисления полученного интеграла воспользуемся формулой:
.
Тогда
.
Для того, чтобы вернуться к исходной переменной, необходимо провести следующие преобразования:
.
Учитывая, что
;
;
,
окончательно получаем:
.
2) Если интеграл
содержит радикал
,
то полагают
.
(1.5)
Следует отметить, что часто, полученный в результате указанной подстановки интеграл, в свою очередь, оказывается довольно сложным. В таком случае можно вместо подстановки (1.5) воспользоваться гиперболической подстановкой
.
(1.6)
При использовании гиперболических подстановок надлежит помнить, что
,
.
3) Интеграл, содержащий
радикал
может быть упрощен путем замен
или
.