
- •12. Общие вопросы теории переходных процессов
- •13.Переходные процессы. Классический метод расчёта переходных процессов
- •14. Переходные процессы. Определение порядка цепи n
- •15. Переходные процессы. Определение корней характеристического уравнения
- •16. Переходные процессы. Определение постоянных интегрирования
- •1 7. Переходные процессы. Разряд заряженной ёмкости через сопротивление r
- •18. Переходные процессы. Подключение r -цепи к источнику постоянного напряжения
- •19. Переходные процессы. Подключение r -цепи к источнику постоянного напряжения
- •4 .2.5.4. Подключение rc-цепи к источнику гармонического напряжения
- •20. Переходные процессы. Разряд заряженной емкости на цепь rl.
- •21. Переходные процессы. Апериодический разряд емкости на цепь rl
- •22. Общий случай расчета цепи II порядка
- •23. Операторный метод расчета переходных процессов в линейных электрических цепях
- •Но стержневые (ключевые) теоремы
- •24. Законы Ома и Кирхгофа в операторной форме
- •25. Эквивалентные операторные схемы
- •26. Порядок расчета переходных процессов операторным методом
- •27. Нахождение оригинала по изображению
- •28. Расчет свободных составляющих операторным методом
20. Переходные процессы. Разряд заряженной емкости на цепь rl.
1.
Независимые начальные условия для
рассматриваемой цепи (рис. 4.15):
![]()
2 . Дифференциальное
уравнение цепи и корни характеристического
уравнения:
. Дифференциальное
уравнение цепи и корни характеристического
уравнения:
![]()
![]() ;
;
![]() .
.
Характеристическое уравнение
![]() или
или
![]() . (4.11)
. (4.11)
Корни характеристического уравнения
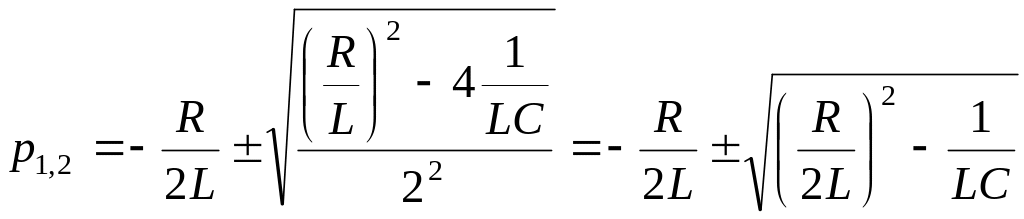 . (4.12)
. (4.12)
3. Полное
решение
![]() .
Вид свободной составляющей и характер
переходного процесса будут определяться
тем, какими числами будут корни
характеристического уравнения. Это
зависит от соотношения между параметрами
цепи, в частности, от подкоренного
выражения в уравнении (4.12). Здесь возможны
три варианта:
.
Вид свободной составляющей и характер
переходного процесса будут определяться
тем, какими числами будут корни
характеристического уравнения. Это
зависит от соотношения между параметрами
цепи, в частности, от подкоренного
выражения в уравнении (4.12). Здесь возможны
три варианта:
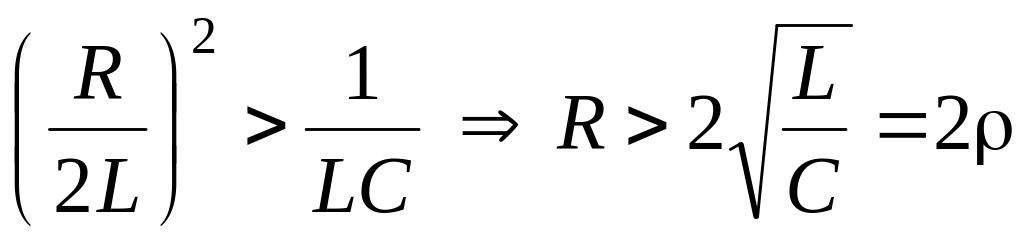 ,
где
– волновое сопр-ние контура, т.е. для
низкодобротных контуров Q
< 0,5. При этом корни p1
и p2
– вещ. отриц. разные.
,
где
– волновое сопр-ние контура, т.е. для
низкодобротных контуров Q
< 0,5. При этом корни p1
и p2
– вещ. отриц. разные.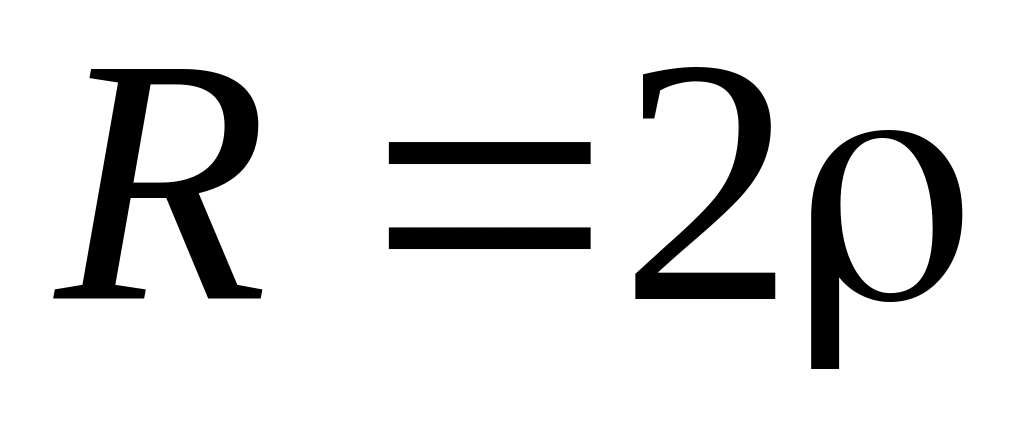 или
Q
= 0,5: корни p1
= p2
– вещественные отриц. равные
или
Q
= 0,5: корни p1
= p2
– вещественные отриц. равные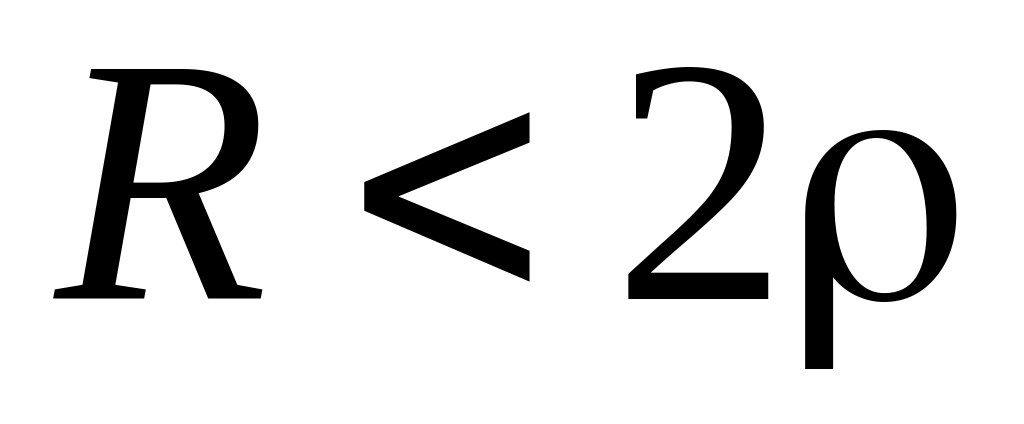 или
Q
> 0,5: корни p1
и p2
– комплексные сопряженные.
или
Q
> 0,5: корни p1
и p2
– комплексные сопряженные.
В первых двух случаях переходный процесс носит апериодический характер (напряжение на емкости uC монотонно затухает до нуля, не меняя своей полярности); в третьем случае процесс разряда – колебательный.
21. Переходные процессы. Апериодический разряд емкости на цепь rl
Рассмотрим
случай, когда p1,2
– действительные
и отрицательные,
т.е.
![]() .
В этом случае переходный процесс
называется апериодическим
и вид полного решения следующий:
.
В этом случае переходный процесс
называется апериодическим
и вид полного решения следующий:
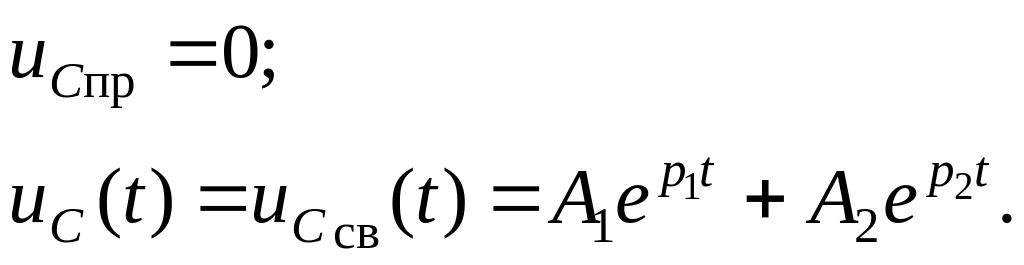
Найдем постоянные интегрирования А1 и А2:
![]() ;
;
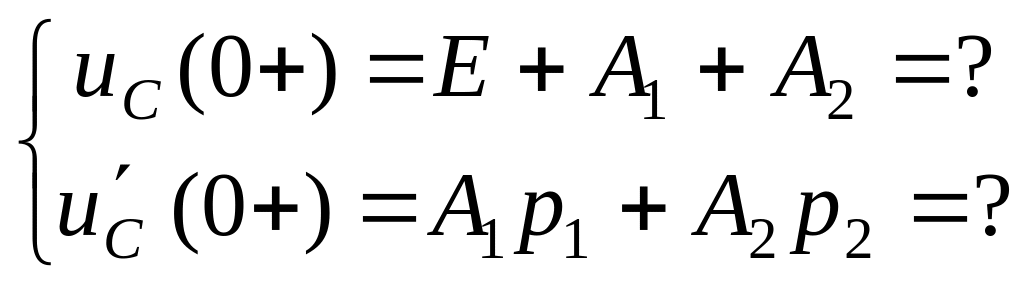
![]()
![]()
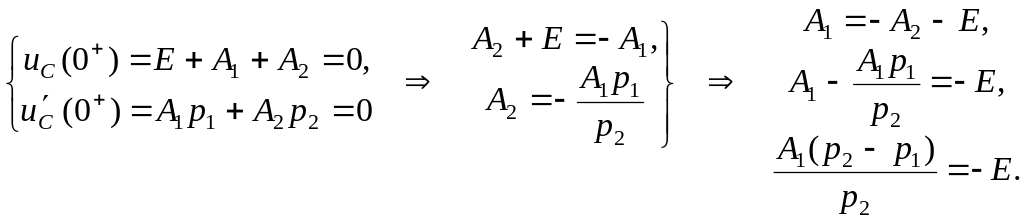
![]() ;
аналогично:
;
аналогично:
![]() .
.
Таким
образом, искомое
![]() имеет
вид:
имеет
вид:
![]() .
.
![]() ;
;
![]() .
.
Качественно изобразим график (рис. 4.15).
Рассмотрим начальные значения:
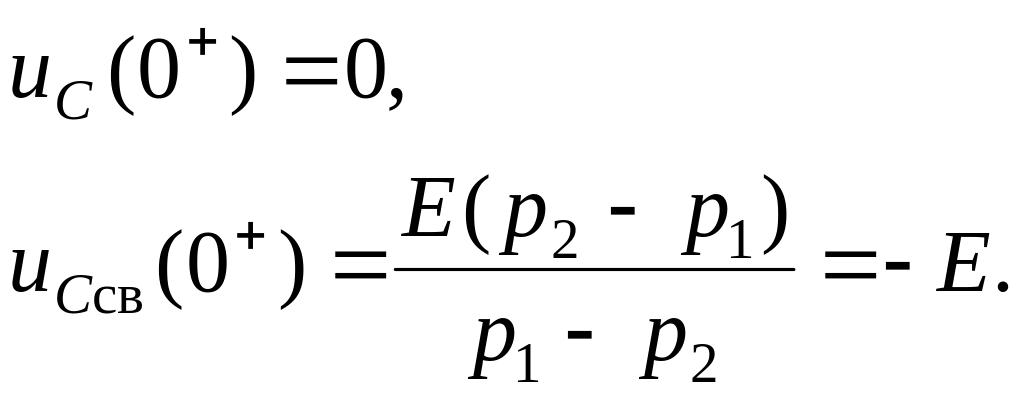
П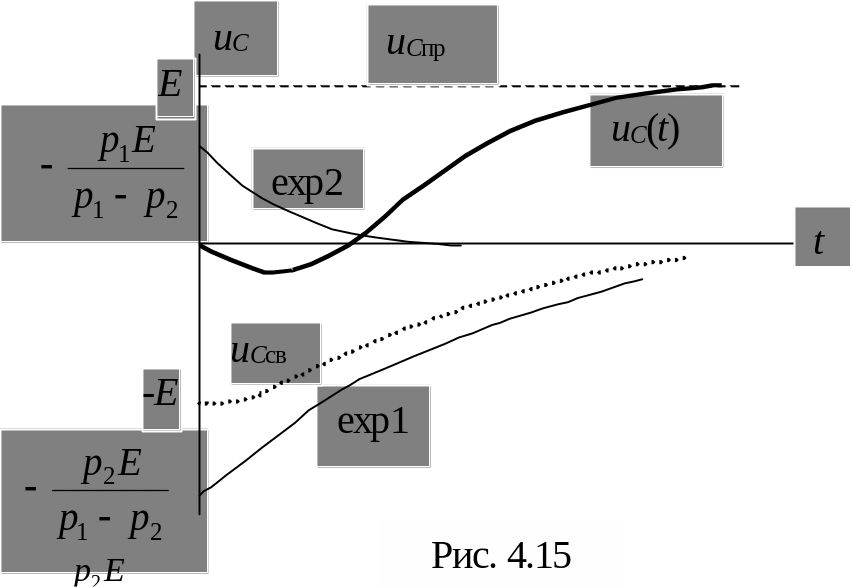 олучим
функцию изменения тока в цепи:
олучим
функцию изменения тока в цепи:
![]() .
.
С
учетом того, что по теореме Виета
![]() ,
,
![]() .
.
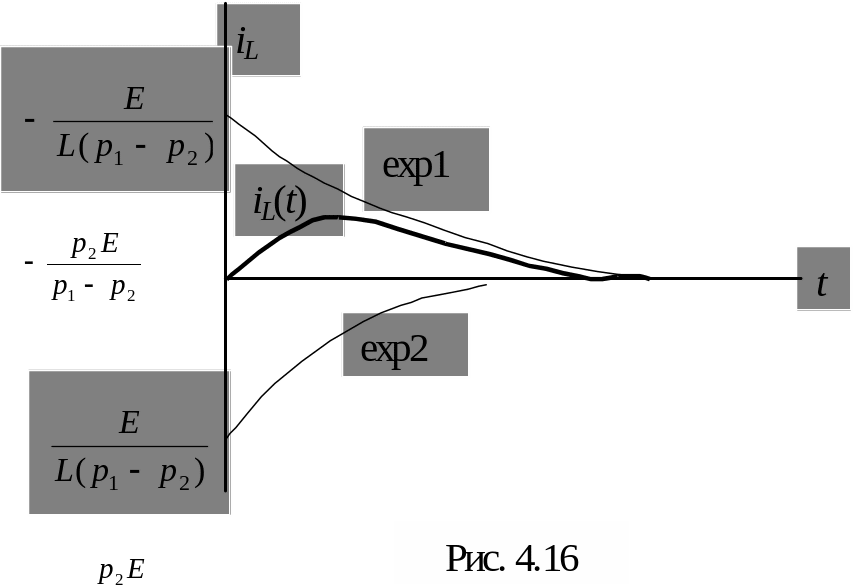
Для
построения графика (рис. 4.16) проведем
аналогичные изложенным выше исследования.
Поскольку
![]() ,
первая экспонента имеет большую
постоянную времени и обращается в нуль
за больший промежуток времени. Так как
,
первая экспонента имеет большую
постоянную времени и обращается в нуль
за больший промежуток времени. Так как
![]() ,
,
![]() ,
,
![]() ,
тогда
,
тогда
![]()
Получим функцию изменения напряжения на индуктивности
![]() .
.
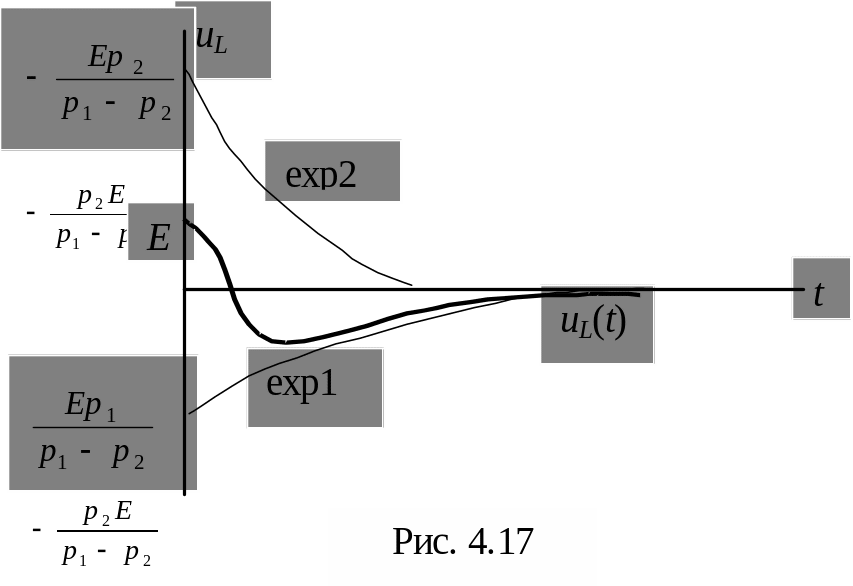
С учетом сказанного выше, exp1 находится в нижней полуплоскости и имеет большую постоянную времени, а exp2 находится в верхней полуплоскости и устремляется к нулю за меньший промежуток времени (рис. 4.17).
Начальные
условия определяются следующим образом
![]() .
Поскольку
,
модули exp1, 2
отличаются на E,
причем exp1(0+) < exp2(0+).
.
Поскольку
,
модули exp1, 2
отличаются на E,
причем exp1(0+) < exp2(0+).
22. Общий случай расчета цепи II порядка
П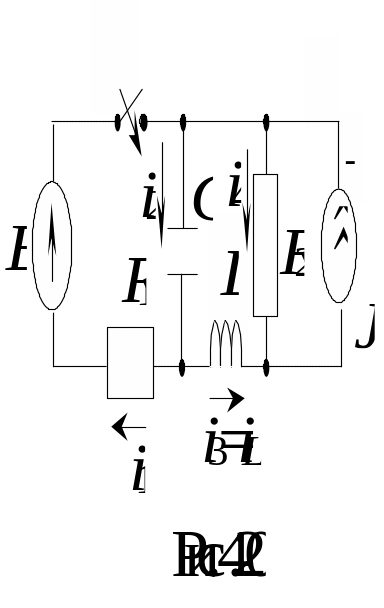 роиллюстрируем
рассмотренную выше методику на примере
цепи второго порядка.
роиллюстрируем
рассмотренную выше методику на примере
цепи второго порядка.
Пусть дана цепь (рис. 4.20) с параметрами Е = 30 В, J = 2 А, R1 = 20 Ом, R2 = 10 Ом, С = 100 мкФ, L = 50 мГн.
Требуется определить закон изменения тока i1(t) после коммутации.
1. Правила коммутации:
iL(0-) = iL(0+) = 0 А,
uC (0-) = uC (0+) = JR2 = 20 B.
2. Составление характеристического уравнения цепи. С помощью совместного решения однородной системы дифференциальных уравнений. Составляем систему дифференциальных уравнений для мгновенных значений токов и напряжений по законам Кирхгофа:
![]()
Методом исключения получаем из данной системы дифференциальное неоднородное уравнение
![]()
Соответствующее ему характеристическое уравнение имеет вид
![]()
Подставим значения параметров цепи:
p2 + 700p + 300000 = 0.
Корни характеристического уравнения
p1 = – 350 + j421,308, p2 = – 350 – j421,308
являются комплексными сопряженными, следовательно, переходный процесс в цепи имеет колебательный характер.
3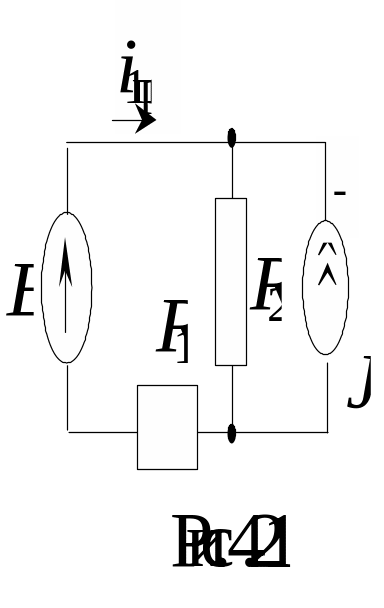 . Определение
принужденной составляющей. Рассматриваемая
цепь в принужденном режиме имеет вид
(рис. 4.21)
. Определение
принужденной составляющей. Рассматриваемая
цепь в принужденном режиме имеет вид
(рис. 4.21)
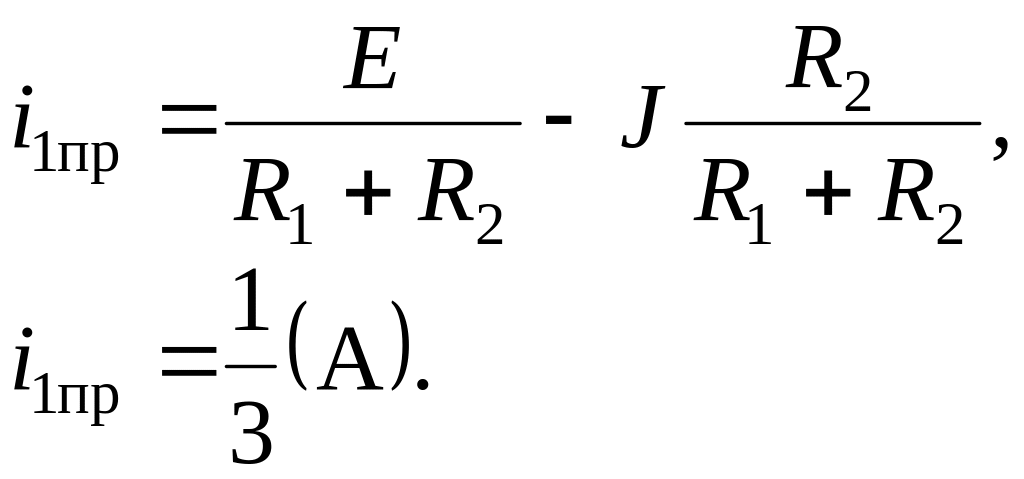
4. Определение свободной составляющей. Для цепей, характеристические числа которых имеют комплексные сопряженные значения, свободная составляющая определяется в виде
![]() ,
,
где – декремент затухания,
– частота
свободных колебаний определяются через
корни характеристического уравнения
![]() .
.
Таким образом, в выражении i1св необходимо определить постоянные интегрирования А1 и А2. Вычисление их ведется с помощью системы уравнений, составленных для момента t = 0+:
![]()
4.1.
Определение значений
![]() и
и
![]() с использованием системы уравнений
Кирхгофа. В данном случае составляется
система уравнений Кирхгофа. Методом
исключения выражается значение тока
через известные значения uC(0+)
и i2(0+):
с использованием системы уравнений
Кирхгофа. В данном случае составляется
система уравнений Кирхгофа. Методом
исключения выражается значение тока
через известные значения uC(0+)
и i2(0+):
![]() .
.
Дифференцируя выражение для i1(t), получим
![]() .
.
Произведя необходимые преобразования и подстановки в системе уравнений Кирхгофа, получим
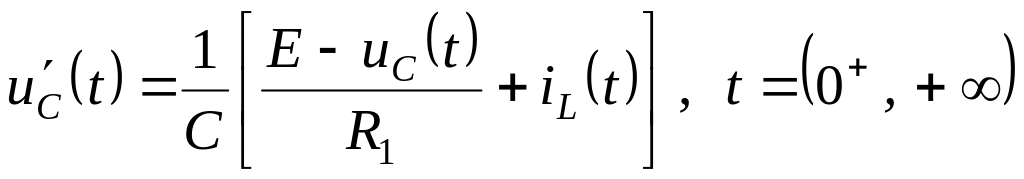 .
.
Подставив
соответствующие значения uC
и iL
в момент t = 0+,
рассчитаем
![]() A/с.
A/с.
4.2. Определение i1(0+) и с использованием резистивных схем замещения в момент t = 0+. При построении схемы замещения в 0+:
–источники с ЭДС или задающим током, номиналы резисторов оставить неизменными;
– емкости
и индуктивности же заменить в соответствии
со следующим правилом: емкости с нулевыми
начальными условиями (![]() )
заменяются короткозамкнутыми участками,
с ненулевыми начальными условиями (
)
заменяются короткозамкнутыми участками,
с ненулевыми начальными условиями (![]() )
заменяются противодействующими
источниками ЭДС с
)
заменяются противодействующими
источниками ЭДС с
![]() ;
;
– ветви
с индуктивностями, имеющими нулевые
начальные условия (![]() ),
размыкаются, в случае ненулевых начальных
условий (
),
размыкаются, в случае ненулевых начальных
условий (![]() )
индуктивности заменяют на содействующие
источники тока с
)
индуктивности заменяют на содействующие
источники тока с
![]() .
.
С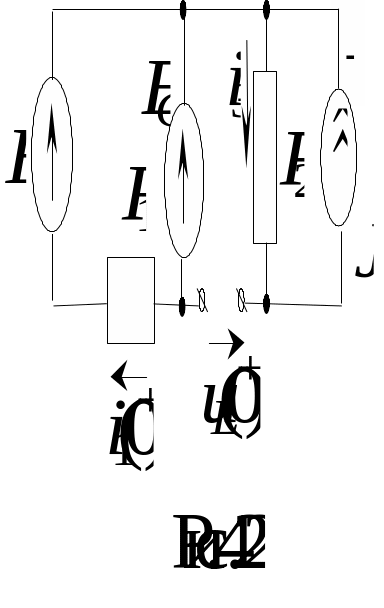 хема
замещения в 0+
для величин токов и напряжений изображена
на рис. 4.22.
хема
замещения в 0+
для величин токов и напряжений изображена
на рис. 4.22.
![]()
По II закону Кирхгофа получим
![]() .
.
Для построения схемы замещения в (0+) для производных токов и напряжений необходимо определить начальные значения:
![]()
Таким образом, следует определить iC(0+) и uL(0+) с помощью уже полученной схемы замещения:
а) для определения uL(0+) составим уравнение по II закону Кирхгофа:
![]() ,
,
подставив
значения, получим uL(0+)
= 0, следовательно,
![]() .
.
б)
iC(0+)
= i1(0+)
= 0,5 A, следовательно,
![]() = 5000 B/с.
= 5000 B/с.
При построении схемы замещения в 0+ для производных следует:
– источники заменить на аналогичные источники с ЭДС или задающим током, равным соответственно производной от данных в задании;
– номиналы резисторов оставить неизменными;
– емкости
и индуктивности же заменить в соответствии
со следующим правилом: емкости с нулевыми
начальными условиями (![]() )
заменяются короткозамкнутыми участками,
с ненулевыми начальными условиями (
)
заменяются короткозамкнутыми участками,
с ненулевыми начальными условиями (![]() )
заменяются противодействующими
источниками ЭДС с
)
заменяются противодействующими
источниками ЭДС с
![]() ;
;
– ветви
с индуктивностями, имеющими нулевые
начальные условия (![]() ),
размыкаются, в случае ненулевых начальных
условий (
),
размыкаются, в случае ненулевых начальных
условий (![]() )
индуктивности заменяют на содействующие
источники тока с
)
индуктивности заменяют на содействующие
источники тока с
![]() .
.
Таким образом, осуществляется операция дифференцирования, адекватная дифференцированию системы уравнений Кирхгофа.
В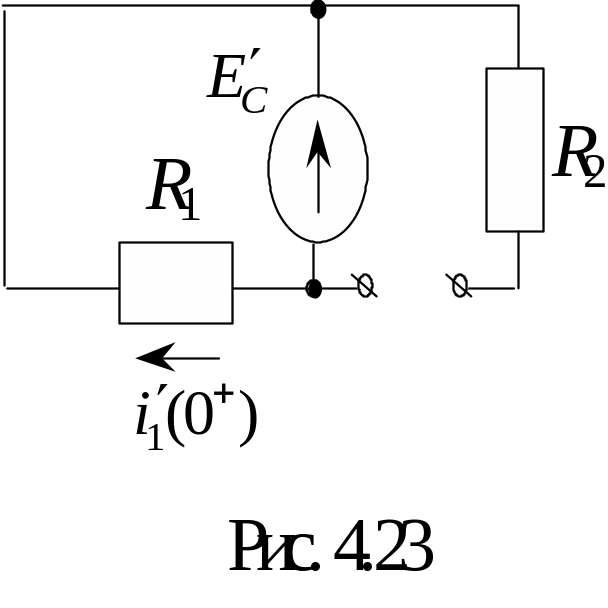 нашем случае, когда в цепи действуют
источники постоянных воздействий,
источники ЭДС заменяются короткозамкнутыми
участками (т.к.
нашем случае, когда в цепи действуют
источники постоянных воздействий,
источники ЭДС заменяются короткозамкнутыми
участками (т.к.
![]() ),
а ветви с источниками тока размыкаются
(т.к.
),
а ветви с источниками тока размыкаются
(т.к.
![]() ).
).
Таким
образом, схема замещения в t
= 0+
для производных имеет вид (рис. 4.23).
Определим
![]() .
.
4.3. Определение постоянных интегрирования:
![]()
Решив данную систему уравнений, получим
А1 = 0,1667, А2 = – 0,455.
5. Определение полного решения. Полное решение следует искать в виде i1(t) = i1пр + i1св.
С учетом произведенных расчетов получим
![]()
Для удобства преобразуем полученное выражение в синусоидальную форму:
![]() .
.
Таким образом, искомый ток изменяется по следующему закону
i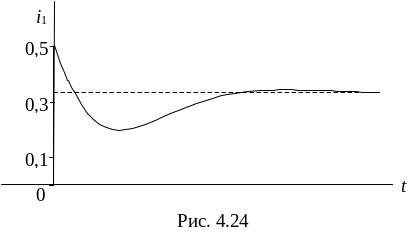 1(t)
= 1/3 + 0,485e-350t
sin(421,308t
+ 2,788).
1(t)
= 1/3 + 0,485e-350t
sin(421,308t
+ 2,788).
График изменения i1(t) представлен на рис. 4.24.
Порядок расчета переходных процессов классическим методом:
расчет принужденной составляющей переходного процесса;
определение корней характеристического уравнения;
определение свободной составляющей переходного процесса в зависимости от полученных корней;
запись полного решения
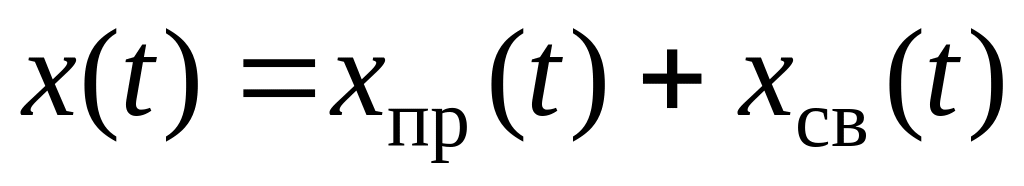 ;
;определение независимых начальных условий (ток в индуктивности и напряжение на конденсаторе) из расчета докоммутационного режима;
определение постоянных интегрирования;
нахождение окончательного решения
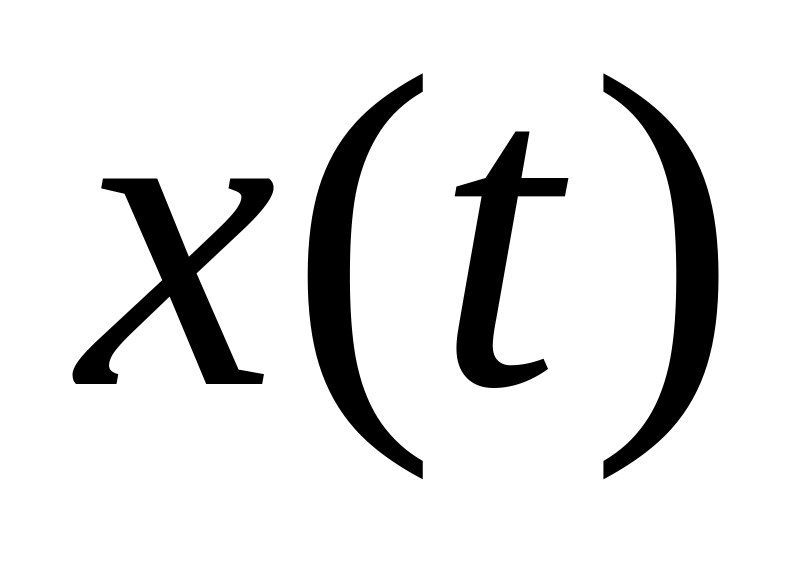 .
.
Классический метод анализа переходных процессов, будучи прозрачным и наглядным, имеет недостатки, связанные с громоздкой процедурой определения начальных условий, которые усугубляются с ростом порядка исследуемой цепи.
