18. Переходные процессы. Подключение r -цепи к источнику постоянного напряжения
1
.
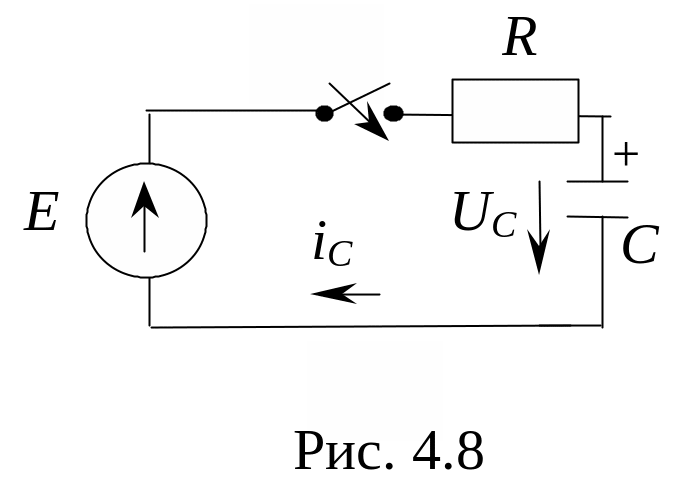Запишем правило коммутации для цепи на
рис. 4.8
.
2. Получим дифференциальное уравнение цепи
+
,
,
,
.
Характеристическое уравнение цепи ,
корень которого .
Постоянная
времени
.
3. Запишем
полное решение
.
Здесь свободная составляющая также включает только одну экспоненту, поскольку цепь имеет первый порядок.
4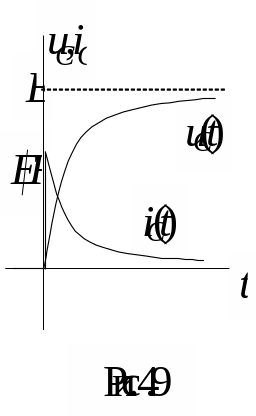
. Подставив
в полное решение t = 0+,
определим постоянную интегрирования
на основании правил коммутации
.
Таким образом, окончательный результат имеет вид
.
Ток
в цепи
.
Графики
изменения
и
представлены на рис. 4.9. Значение тока,
содержащее лишь свободную составляющую,
максимально в начальный момент времени,
когда оно скачком достигает значение
,
и все напряжение источника приложено
к резистору. По мере зарядки конденсатора
напряжение на нем повышается, что ведет
к соответственному уменьшению тока в
цепи.
19. Переходные процессы. Подключение r -цепи к источнику постоянного напряжения
1. Запишем правило коммутации для цепи на рис. 4.10
.
2. Получим дифференциальное уравнение цепи
,
,
характеристическое уравнение
.
Корень характеристического уравнения и постоянная времени соответственно
,
.
3. Полное решение имеет вид:
.
4. Подставив в iL(t) t = 0+ на основании правила коммутации определим постоянную интегрирования
.
Таким образом,
.
Напряжение на индуктивности
.
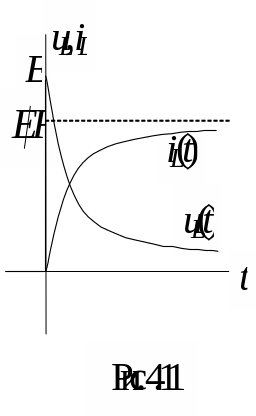
Графики изменения uL(t),
iL(t)
приведены на рис. 4.11.
4 .2.5.4. Подключение rc-цепи к источнику гармонического напряжения
Рассмотрим случай, когда в цепи (рис. 4.12) действует источник синусоидальной ЭДС
.
Здесь
– фаза включения, т.к. она определяется
моментом срабатывания коммутатора.
Интуитивно следует ожидать влияние
на качественную и количественную картину
протекания переходного процесса.
Порядок расчета переходных процессов, описанный выше, не претерпевает никаких изменений.
1. Запишем правило коммутации
.
2. Дифференциальное уравнение и соответствующее ему характеристическое уравнение:
.
Корень характеристического уравнения
.
3. Полное решение для рассматриваемой цепи первого порядка
.
4. Расчет принужденной составляющей произведем символическим методом
;
;
;
.
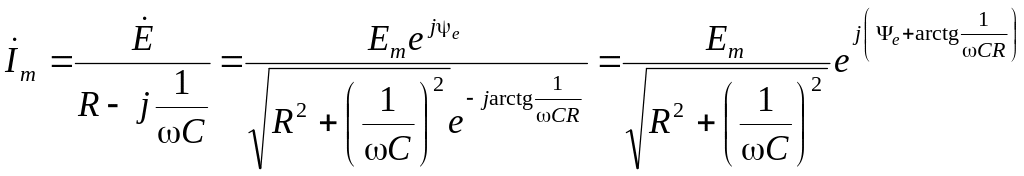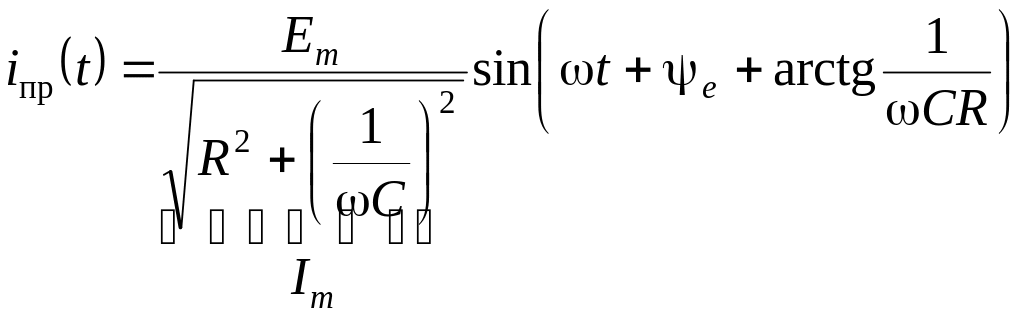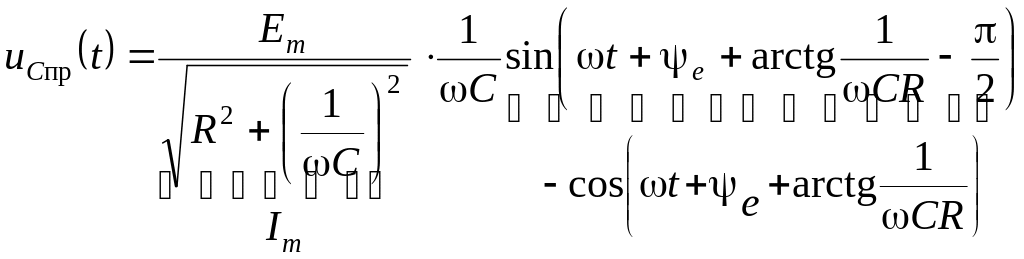5. Для расчета постоянной интегрирования запишем полное решение для момента t = 0+
;
.
В соответствии с правилом коммутации
;
Таким образом,
или
.
Определим
;
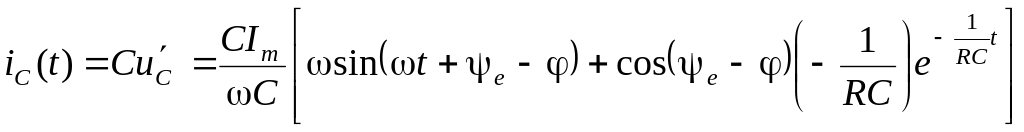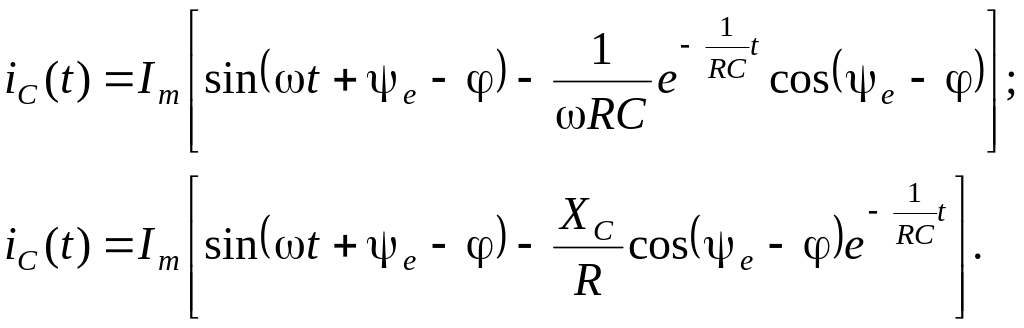
Оба
выражения для uC
и
iC
в общем случае имеют периодическую
принужденную и апериодическую свободную
составляющие. При этом характер
переходного процесса существенно
зависит от двух факторов – начальной
фазы напряжения источника в момент
включения
и соотношения параметров цепи
и R.
Исследуем ожидаемое влияние фазы включения источника на переходный режим
1)
Пусть
,
тогда
.
Поскольку cos 0 = 1,
получим
.
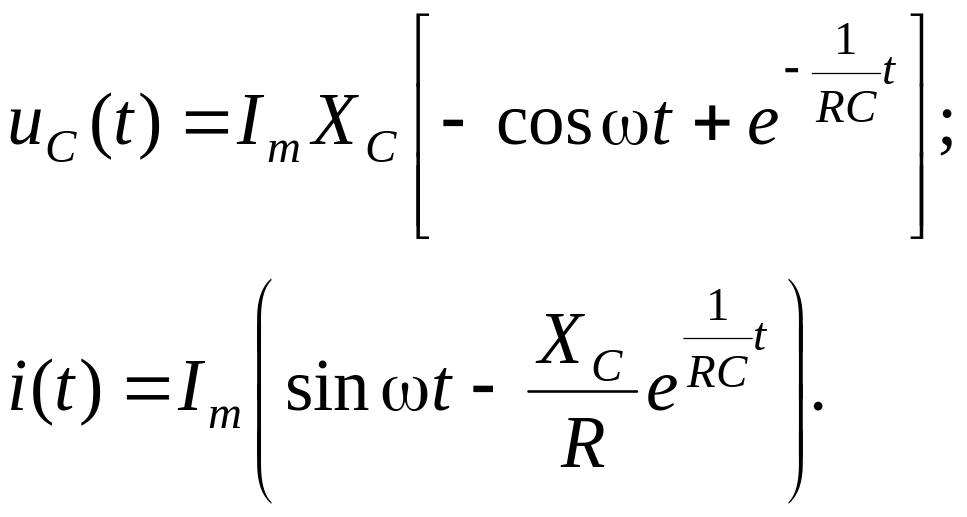
а) исследование
кривой напряжения (рис. 4.13) наглядно
демонстрирует, что максимальное
напряжение в переходном режиме ограничено
.
б) исследование кривой тока (рис. 4.14).
Максимальное значение тока в переходном режиме зависит от соотношения и R и может превышать Imпр в несколько раз. Однако этот начальный всплеск тока является кратковременным.
2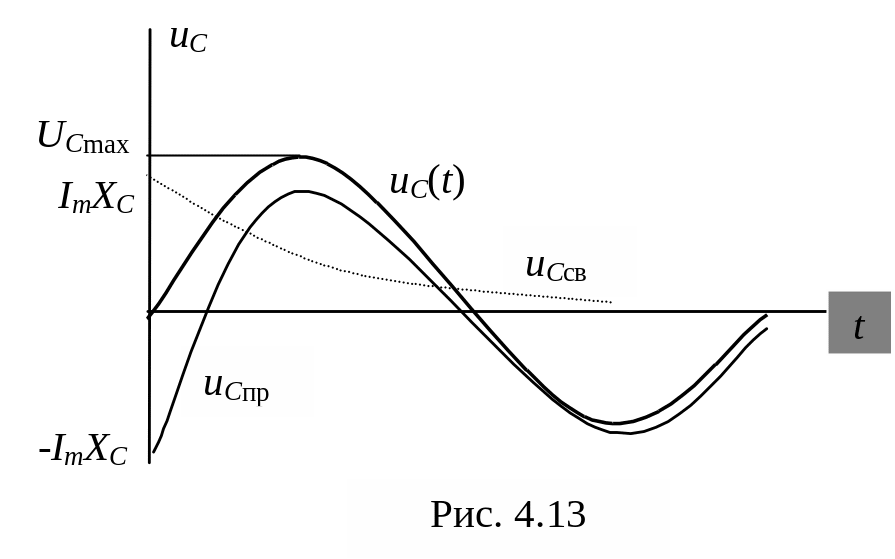
)
В случае, если
,
поскольку
,
получим
Т
аким
образом, в данном случае в цепи переходный
процесс не н