16. Переходные процессы. Определение постоянных интегрирования
Как известно, постоянные интегрирования определяются из начальных условий, каковыми являются значения искомой функции и ее производных по (n – 1)-ую включительно в начальный момент времени 0+ («справа»). В отличие от чисто математических задач, где эти условия задаются в качестве исходных данных непосредственно, при анализе переходных процессов задаются начальные условия «слева» в момент t = 0–, предшествующий коммутации (чаще всего они формулируются самой постановкой задачи и легко определяются из расчета докоммутационного режима). Нахождение начальных условий «справа» по известным значениям начальных условий «слева» – ключевой момент в расчете переходных процессов.
Опишем процедуру отыскания начальных условий в цепи n-го порядка
для послекоммутационной схемы (
)
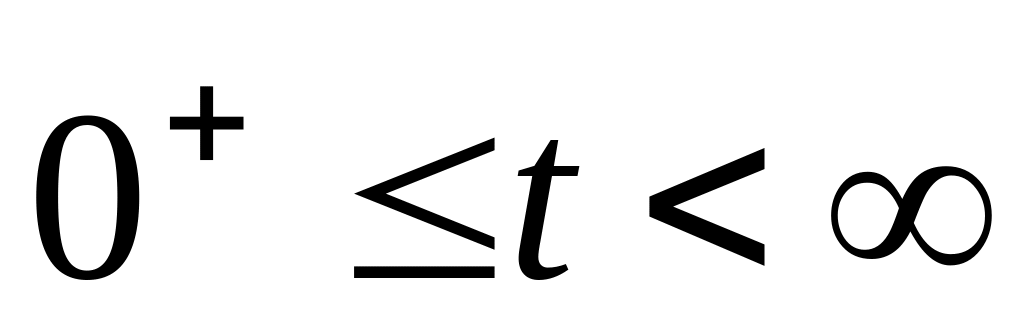составляют систему уравнений для
мгновенных значений токов и напряжений
по законам Кирхгофа, дополняют эту
систему компонентными уравнениями
типа
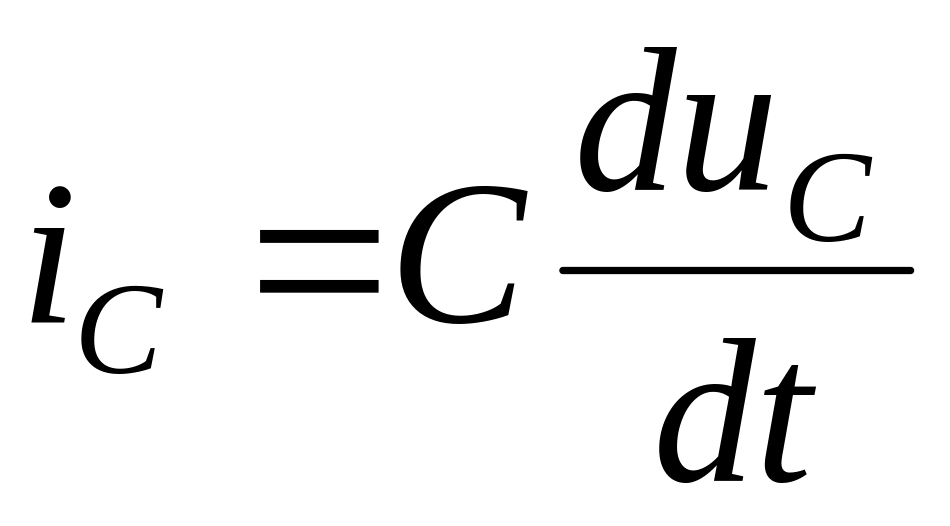для емкости;
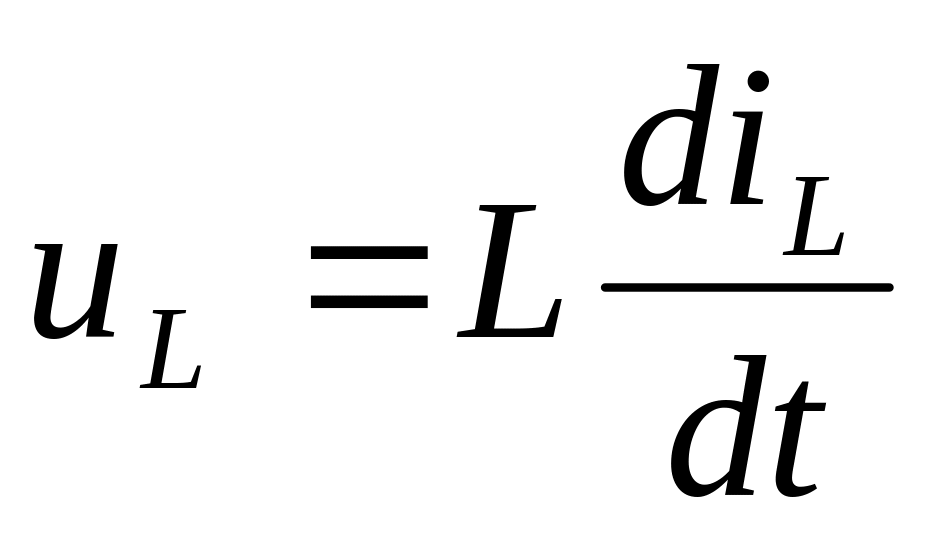для индуктивности;рассматривают эту систему уравнений в момент t = 0+ с учетом независимых начальных условий, которые по правилам коммутации берутся равными начальным условиям «слева», в результате определяются зависимые начальные условия, в том числе значения первых производных от индуктивных токов и емкостных напряжений;
для отыскания значений первых производных от зависимых электрических величин и вторых производных от независимых электрических величин необходимо систему уравнений из п. 1 продифференцировать и рассмотреть ее в момент t = 0+ с учетом информации, полученной в п. 2;
процедура дифференцирования продолжается до тех пор, пока не будет найдена (n – 1)-ая производная искомой функции в 0+.
Система уравнений для определения постоянных интегрирования имеет следующий вид:
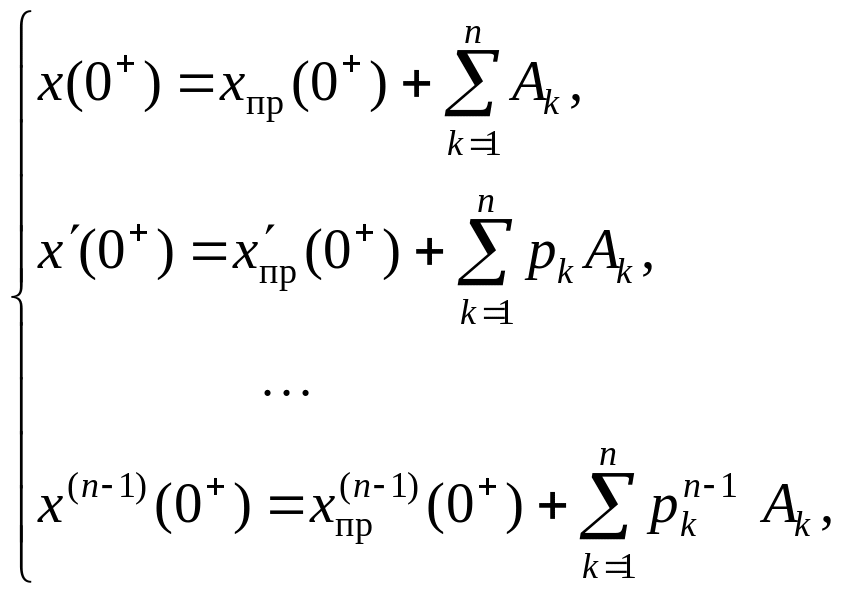(4.9)
Здесь для определенности полагаем все корни pk вещественными разными числами. Кроме того, следует учитывать, что при наличии в цепи только источников постоянных воздействий значение производных от принужденной составляющей переходного процесса равны нулю.
Возможная схемная реализация этой технологии подробно описана в [] и позже будет пояснена на конкретном примере.
1 7. Переходные процессы. Разряд заряженной ёмкости через сопротивление r
1. Запишем правило коммутации для цепи на рис. 4.5:
.
2. Составим дифференциальное уравнение цепи:
;
.
Характеристическое уравнение первого порядка:
,корень
которого
.
3. Полное решение дифференциального уравнения:
.
Поскольку
уравнение имеет первый порядок, свободная
составляющая имеет одну экспоненту
.
4. Определим
принужденную составляющую
.
5. Для определения постоянной интегрирования A запишем полное решение для момента t = 0+
.
Применив правило коммутации, получим окончательное решение
.
Ток в цепи определяется с помощью дифференциального закона Ома
,
, 
.
Итак,
имеем две экспоненты, описывающие
изменения
и
.
Графики изменения
и
представлены на рис. 4.6. Напряжение на
конденсаторе непрерывно в момент
коммутации и уменьшается по экспоненциальному
закону от начального значения U0.
Знак «минус» в выражении для тока говорит
о том, что ток при разряде конденсатора
направлен противоположно току при его
заряде. В начальный момент значение
тока максимально, его спад связан с
уменьшением напряжения на элементах
цепи. Ток на ёмкости меняется скачком.
В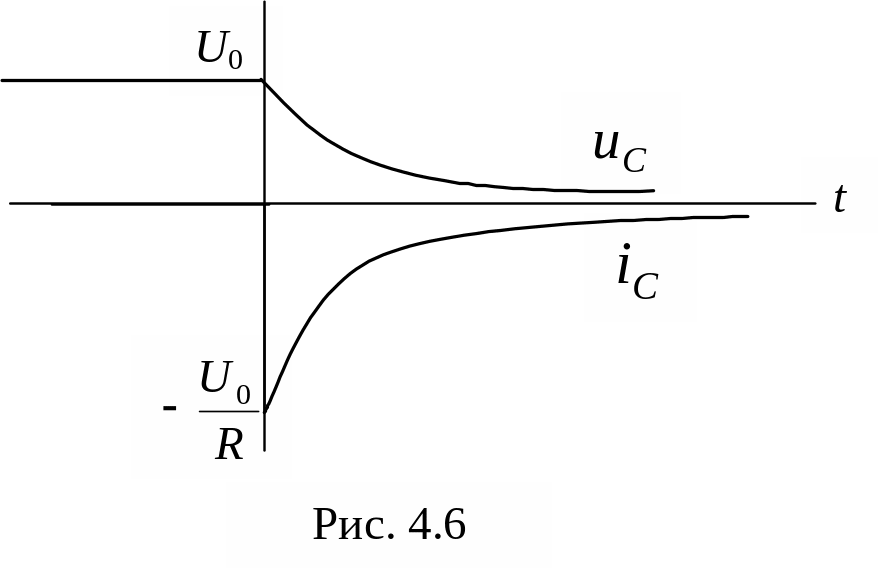
ведём
величину, характеризующую скорость
изменения электрической величины в
переходном режиме, называемую постоянная
времени ().
Величина
показывает, за какой промежуток времени
свободная составляющая переходного
процесса уменьшается в
раз.
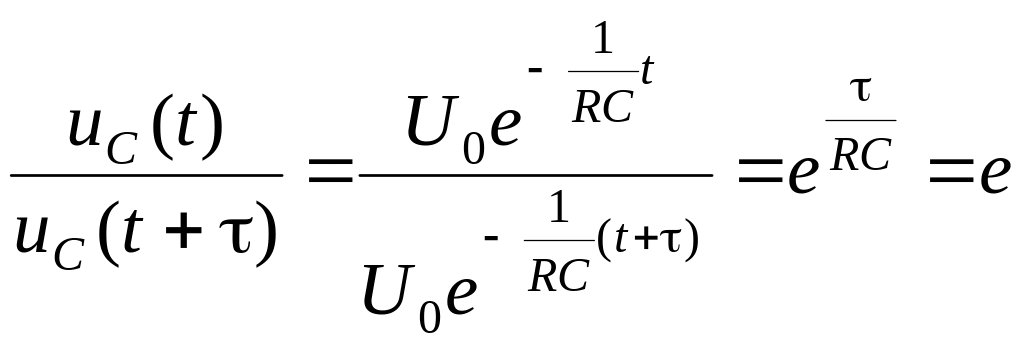
Чем
больше
,
тем медленнее переходный процесс, тем
больше
.
Хотя полученные выше выражения определяют
бесконечную длительность переходного
процесса – свободные составляющие лишь
асимптотически стремятся к нулю –
практически можно считать, что переходный
процесс заканчивается за время, равное
.
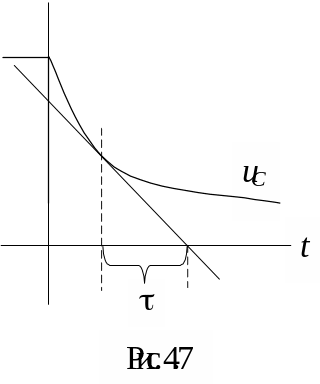
Постоянную времени можно графически определить по длине подкасательной, проведённой в любой точке свободной составляющей переходного процесса (рис. 4.7).
Постоянная
времени измеряется в секундах и для
цепей первого порядка связана с корнем
характеристического уравнения
.
(4.10)
Рассмотрим энергетические соотношения, описывающие работу цепи после коммутации.
Энергия
электрического поля конденсатора до
коммутации –
,
в результате полного разряда при
.
Покажем, что вся энергия, запасенная в конденсаторе, выделяется в виде тепловой энергии на резисторе R:
