Верификация имитационной модели

Верификация – доказательство утверждений соответствия алгоритма ее функционирования замыслу моделирования и своему назначению. На этапе верификации устанавливается верность логической структуры модели, реализуется комплексная отладка с помощью средств трассировки, ручной имитации – проверяется правильность реализации моделирующего алгоритма.

Комплексные процедуры верификации включают неформальные и формальные исследования программы-имитатора. Неформальные процедуры могут состоять из серии проверок. Серии проверок:

а) проверка преобразования информации от входа к выходу;

б) трассировка модели на реальном потоке данных (при заданных G и X):

- X изменяется по всему диапазону значений – контролируется Y,

- можно посмотреть, не будет ли модель давать абсурдные ответы, если ее параметры будут принимать предельные значения,

в) “проверка на ожидаемость” заменяют стохастические элементы на детерминированные и др.

Формальные процедуры связаны с проверкой исходных предположений (выдвинутых на основе опыта, теоретических знаний,интуитивных представлений, на основе имеющейся информации). Общая процедура включает:

а) построение ряда гипотез о поведении системы и взаимодействии ее элементов;

б) проверка гипотез с помощью статистических тестов: используют методы статистической теории оценивания и проверки гипотез (методы проверки с помощью критериев согласия (², Колмогорова-Смирнова, Кокрена и др.), непараметрические проверки и т.д., а также дисперсионный, регрессионный, факторный, спектральный анализы).

Валидация имитацинной модели

Наиболее существенные процедуры исследования свойств модели:

• оценка точности результатов моделирования,

• оценка устойчивости результатов моделирования,

• оценка чувствительности ИМ (т.е. зависимости изменения Y от изменения Х), т. е. чувствительность критериев качества к изменению параметров модели.

Методика оценки устойчивости:

В модельном времени с шагом t контролируются выходные параметры Y. Оценивается амплитуда изменений параметра Y.

Рост разброса контролируемого параметра от начального значения при изменении t +t указывает на неустойчивый характер имитации исследуемого процесса.

Для проверки статистической гипотезы о равенстве дисперсий значений откликов ИМ ( ) для испытаний с различными длительностями прогонов может быть использован критерий Бартлетта:

, где

Методика несмещенной оценки к-дисперсий нормальных генеральных совокупностей:

1. Устанавливается длительность прогона (0, t^мод)

2. Выбирается контролируемая компонента вектора отклика у_i

3. Задается шаг t,

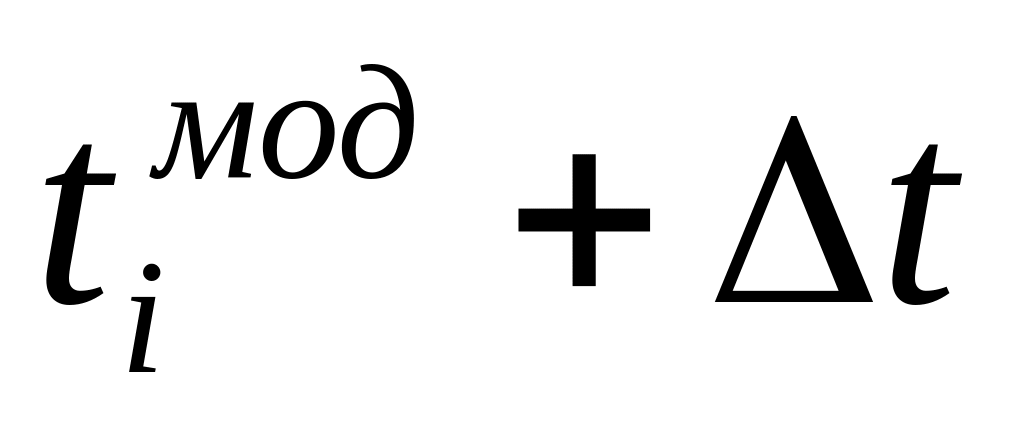
4. На каждом шаге контролируется у_i, оценивается дисперсия 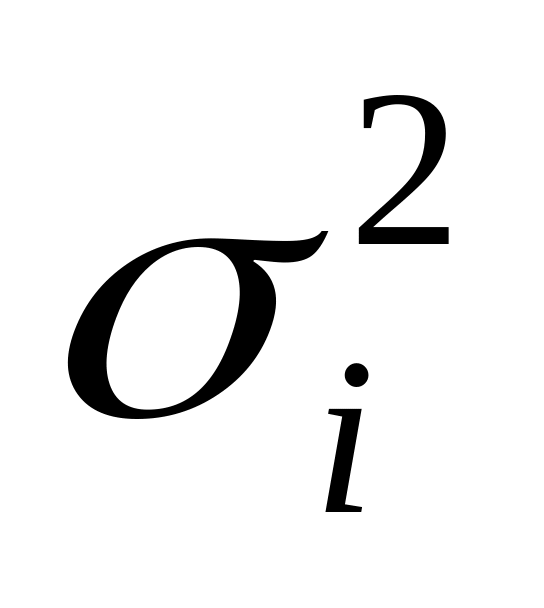и т.д.

5. Формулируется нулевая статистическая гипотеза: о равенстве дисперсий и проверяется с помощью критерия Бартлетта.

6. В_расч сравнивается с тестовой. Если В> χ² , то Н₀ принимается. Считается, что модель устойчива по i- компоненте вектора отклика.

7. и т.д. по всем компонентам

8. В случае удачной проверки, считается что модель устойчива по всему вектору выходных переменных.