§2. Наймовірніше число успіхів у схемі Бернуллі

Означення 1. Найімовірнішим числом m₀ появи події А в n незалежних випробовуваннях називається число, для якого ймовірність не менша ймовірності кожного з решти можливих варіантів, тобто

^.

Якщо найімовірніше число , то повинні виконуватись такі умови:

. (1)

. (2)

З нерівності (1) отримується:

звідки (після скорочень)

Розв’язуючи нерівність відносно , отримують:

. (3)

Аналогічно з нерівності (2) отримується:

Звідки

; . (4)

Остаточно отримується нерівність:

. (5)

Зауваження. Довжина інтервалу, що визначається нерівністю (5), рівна одиниці:

тому, коли межі інтервалів є дробові числа, то отримується одне значення наймовірнішого числа , якщо ж межі є цілими числами, то отримується два значення наймовірнішого числа успіхів

Приклад 1. При даному технологіному процесі 90% всієї продукції – вищого сорту. Знайти наймовірніше число виробів вищого сорту в партії з 200 виробів.

Рішення. За умовою n=200, p=0,9, q=0,1

Тоді ,

.

Отже .

Приклад 2. Гральний кубик кидають 35 раз. Яке найвірогідніше число випадання грані з одиницею?

Рішення. В цьому прикладі n=35, p= ,q= , тому

, де ,

Тому - найвірогідніших значень два.

§3. Граничні теореми теорії ймовірності

1. Локальна теорема Муавра-Лапласа

Очевидно, що користуватись формулою Бернуллі при великих значеннях n досить важко, бо формула вимагає виконання дій над великими числами. Виникає питання, чи можна обчислити ймовірність, не звертаючись до формули Бернуллі? Можна, застосовуючи локальну теорему Лапласа, що дає асимптотичну (наближену) формулу, яка визначає наближену ймовірність появи події рівно m раз в n випробовуваннях, якщо число випробовувань досить велике.

Теорема 1. (локальна теорема Лапласа). Якщо ймовірність р появи події А в кожному випробовуванні постійна (0<p<1), то ймовірність того, що подія А відбудеться в випробовуваннях рівно раз, наближено рівна (тим точніше, чим більше ) значенню функції

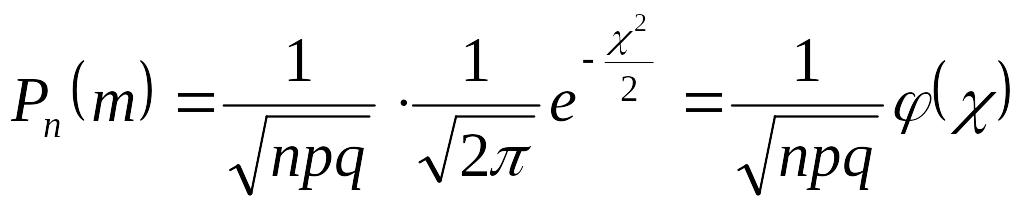
при

Функція Лапласа табульована, причому таблиці складені лише для додатніх значень аргументу, оскільки функція

парна (див. табл. 1).

Приклад 1. Знайти ймовірність того, що подія А відбудеться 90 раз в 400 випробовуваннях, якщо ймовірність появи цієї події в кожному випробовуванні рівна р=0.2.

Рішення. За умовою

2. Інтегральна ознака Муавра-Лапласа

Нехай проволиться n випробувань, в кожному з яких ймовірність появи події А постійна і рівна . Потрібно обчислити ймовірність того, що в випробовуваннях подія А відбудеться не менше раз і не більше раз (від до раз).

Теорема 2. (Інтегральна ознака Муавра-Лапласа). Якщо ймовірність р появи події А в кожному випробовуванні постійна , то ймовірність того, що подія А відбудеться в випробовуваннях від ₁ до раз, наближено рівна:

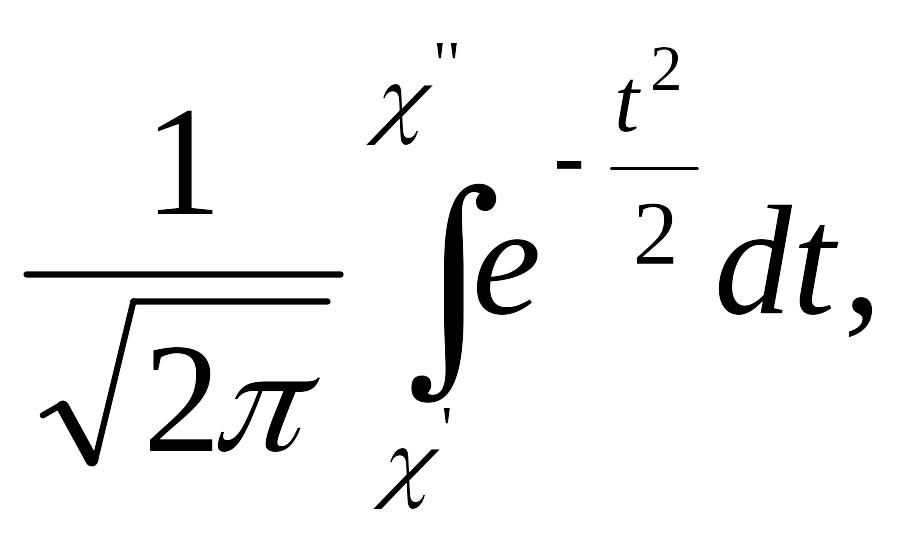
де

При розв’язанні задач, що потребують застосування інтегральної теореми, користуючись спеціальними таблицями, оскільки неозначений інтеграл не виражається через елементарні функції.

Таблиця для інтегралу 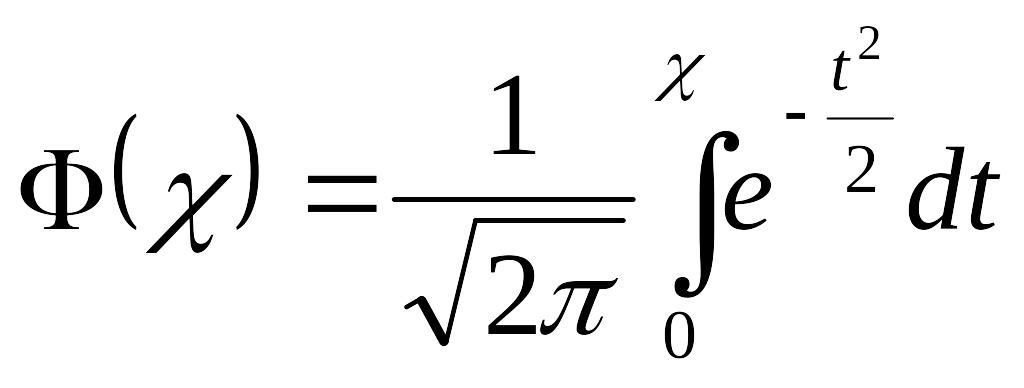наведена в кінці книги (дод.1, таб.2). В таблиці дано значення функції для , оскільки (функція непарна). В таблиці, крім того, дані значення лише до , бо

Отже,

де

Приклад 2. Підприємство дає 99,2% стандартних виробів. Яка ймовірність того, що серед 5000 наугад вибраних виробів цього підприємства число нестандартних менше 60?

Рішення. Ймовірність вибрати нестандартний виріб при

Тому