§2. Формула повної ймовірності. Формула Байеса

Нехай А – деяка подія, яка може відбутись або не відбутись одночасно з однією з подій Н₁, Н₂,...Н_n, що утворюють повну групу несумісних подій . Події Н₁, Н₂,...Н_n називають гіпотезами. Ймовірності всіх гіпотез відомі Р(Н_і) (і= ), а також відомі умовні ймовірності події А при кожній гіпотезі, тобто дано: .

Тоді ймовірність події А визначається теоремою.

Теорема 1. (формула повної ймовірності). Ймовірність події А, що може відбутись разом з однією з гіпотез Н₁, Н₂,...Н_n, дорівнює сумі добутків ймовірності кожної з гіпотез на відповідну умовну ймовірність події А:

. (1)

Доведення. Так як гіпотези Н₁, Н₂,...Н_n утворюють повну групу подій, то подію А можна записати як: , а оскільки несумісні, то:

.

Теорема доведена.

До цих пір розглядалася ймовірність події до випробовування, тобто в комплексі умов не був присутній результат проведеного випробовування.

Тому поставимо тепер наступну задачу. Є повна група несумісних гіпотез Н₁, Н₂, ...Н_n. Відомі ймовірності кожної з гіпотез . Проводиться випробування і в його результаті відбувається подія А, ймовірності якої по кожній гіпотезі відомі, тобто .

Виникає питання, які ймовірності мають гіпотези H_i в зв’язку з появою події А? Тобто були відомі ймовірності апріорні (від латинського a priori – до випробовування). Якщо ж подія А відбулася, то чи можна переоцінити ймовірності кожної з гіпотез ? Ці нові ймовірності будуть вже апостеріорними ймовірностями гіпотез (від латинського a posteriori – після випробовування).

Відповідь на це питання дає теорема Байеса.

Теорема 2. Ймовірність гіпотези після випробовування рівна добутку ймовірності гіпотези до випробовування на відповідну їй умовну ймовірність події, яка відбулася в результаті випробовування, поділеній на повну ймовірність цієї події:

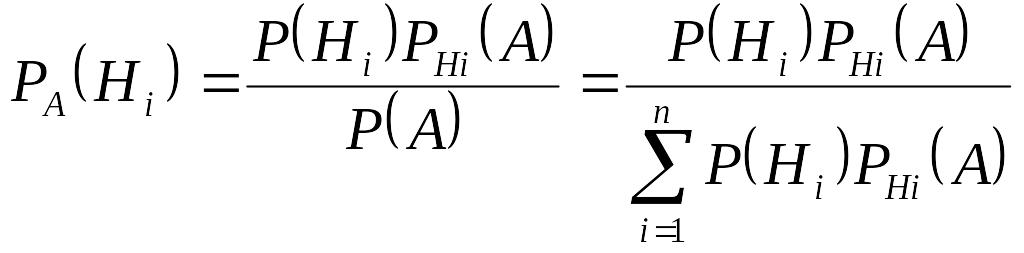. (2)

Доведення. З аксіоми множення ймовірностей випливає:

Звідки

Теорема доведена.

Приклад 1. До магазину надходять вироби з двох заводів, причому з першого 150 штук, а з другого 250. Перший завод випускає в середньому 0.5% бракованої продукції, другий – 0.2%. Яка ймовірність купити в магазині бракований виріб?

Рішення. Нехай подія А є купівля бракованого виробу, гіпотеза Н₁ – виріб, випущений першим заводом, гіпотеза Н₂ – другим заводом. Тоді

По формулі повної ймовірності:

Приклад 2. Спеціалізована лікарня приймає в середньому 50% хворих, що мають захворювання Н₁, 30% - захворювання Н₂ і 20% - Н₃. Статистика свідчить, що ймовірність повного виліковування хвороби Н₁ дорівнює 0.9, для хвороби Н₂ – 0.7 і для хвороби Н₃ – 0.8. Яка ймовірність того, що пацієнт, виписаний з лікарні цілком здоровим (подія А), був хворий на хворобу Н₂?

Рішення.

Згідно формули Байеса

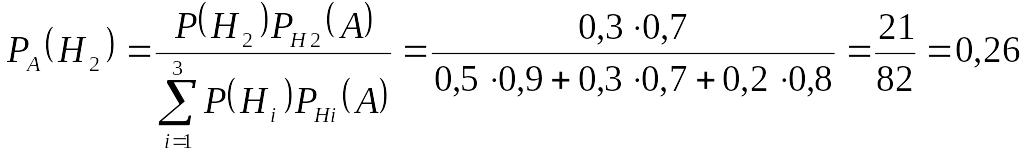
Лекція 3. ПОСЛІДОВНІ НЕЗАЛЕЖНІ ВИПРОБУВАННЯ

§1. Схема Бернуллі

Нехай проводиться серія випробувань, в результаті якої може відбутись подія А з певною ймовірністю. Якщо ймовірність події А в кожному випробуванні не залежить від результатів інших випробувань, то такі випробування називаються незалежними відносно події А.

Поставимо задачу.

Знайти ймовірність того, що в результаті проведення n незалежних випробувань подія А відбудеться рівно m раз, якщо в кожному із цих випробувань дана подія відбувається з постійною ймовірністю ^.

Шукану ймовірність позначають . Наприклад, означає ймовірність того, що при 8-ми випробуваннях подія А відбудеться 4 рази.

Такі випробування називають послідовними незалежними випробовуваннями Бернуллі. Прикладами можуть бути послідовні підкидання монети (подія А – випадання герба, ), послідовні підкидання грального кубика (подія А – випадання 5 очок, ).

Дану задачу можна розв’язати з допомогою теорем додавання і множення ймовірностей, але це призводить до дуже громіздких обчислень.

Тому виникає необхідність застосування простіших методів розрахунку. Одним з таких методів є формула Бернуллі.

Нехай в однакових умовах проводиться n випробувань, результатом кожного з них подія А може відбутися з ймовірністю , або ж з ймовірністю . Позначимо через появу події А в і-му випробуванні. Тоді:

,

Нас цікавить ймовірність того, що подія А при n випробуваннях відбудеться m раз, а в решті n-m випробуваннях відбудеться подія (подія А не відбудеться).

Так як подія А в n випробуваннях може появитись m раз в різних послідовностях або комбінаціях, то число таких комбінацій є .

Наприклад, така сполука (позначимо її подіїю В) є:

коли подія А відбулася m раз підряд, починаючи з першого випробування.

Знайдемо її ймовірність:

Так як всі комбінації події, аналогічні комбінації В, є подіями

несумісними і нам байдуже, в якій саме послідовності з’явиться подія А та , то, застосовуючи теорему додавання ймовірностей для несумісних подій, отримаємо:

. (1)

Формула (1) носить назву формули Бернуллі і має важливе значення в теорії ймовірності, бо вона зв’язана з повторенням випробувань в однакових умовах, тобто з такими умовами, в яких якраз і проявляються закони теорії ймовірності.

Набір чисел називається біномним розподілом, а саму формулу (1) називають біномною, оскільки її права частина є загальним членом розкладу бінома Ньютона . Зауважимо, що події є попарно несумісні, тому

тобто

Приклад 1. Податкова адміністрація виявила, що 40% декларацій про доходи осіб – платників податку – містить принаймі одну похибку. Яка ймовірність того, що з 10 наугад відібраних декларацій, 4 буде з похибкою?

Рішення. Ймовірність, що декларація має похибку а . Тоді: