Контрольна робота
1.
Інвестиційна кампанія має
пакетів акцій, серед яких
пакетів цукрових заводів. Визначити
ймовірність, що серед навмання вибраних
пакетів акцій є рівно
пакетів цукрових заводів.
Задачу
розв'язати за даними таблиці (
―
номер варіанта ):
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
10 |
10 |
10 |
10 |
9 |
11 |
11 |
11 |
10 |
9 |
11 |
10 |
9 |
11 |
|
6 |
5 |
7 |
8 |
7 |
8 |
7 |
6 |
5 |
6 |
7 |
6 |
8 |
8 |
|
3 |
2 |
4 |
4 |
4 |
3 |
2 |
3 |
4 |
4 |
2 |
3 |
2 |
2 |
|
4 |
4 |
5 |
6 |
5 |
4 |
3 |
5 |
5 |
5 |
4 |
6 |
5 |
4 |
|
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
|
12 |
10 |
14 |
12 |
12 |
14 |
10 |
11 |
10 |
14 |
12 |
13 |
12 |
10 |
|
7 |
8 |
5 |
5 |
7 |
7 |
8 |
6 |
6 |
7 |
8 |
7 |
8 |
8 |
|
3 |
2 |
2 |
3 |
4 |
3 |
2 |
2 |
2 |
3 |
2 |
4 |
4 |
2 |
|
6 |
6 |
5 |
6 |
6 |
4 |
3 |
4 |
5 |
6 |
4 |
6 |
6 |
4 |
2.В
двох партіях відповідно
і
якісних виробів. Навмання вибирають по
одному виробу з кожної партії. Яка
ймовірність того, що серед відібраних
виробів: а) хоча б один бракований; б)
обидва браковані; в) один бракований і
один якісний?
Задачу розв'язати за даними таблиці ( ― номер варіанта ):
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
76 |
83 |
75 |
84 |
36 |
44 |
33 |
81 |
73 |
32 |
82 |
43 |
76 |
82 |
|
42 |
35 |
43 |
34 |
82 |
74 |
85 |
37 |
45 |
86 |
36 |
75 |
42 |
36 |
|
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
|
56 |
73 |
65 |
64 |
46 |
44 |
23 |
82 |
63 |
42 |
72 |
53 |
66 |
72 |
|
32 |
45 |
33 |
34 |
72 |
64 |
75 |
26 |
35 |
76 |
36 |
65 |
32 |
26 |
В магазин надходять однотипні вироби з трьох заводів, причому з
-го
заводу надходить
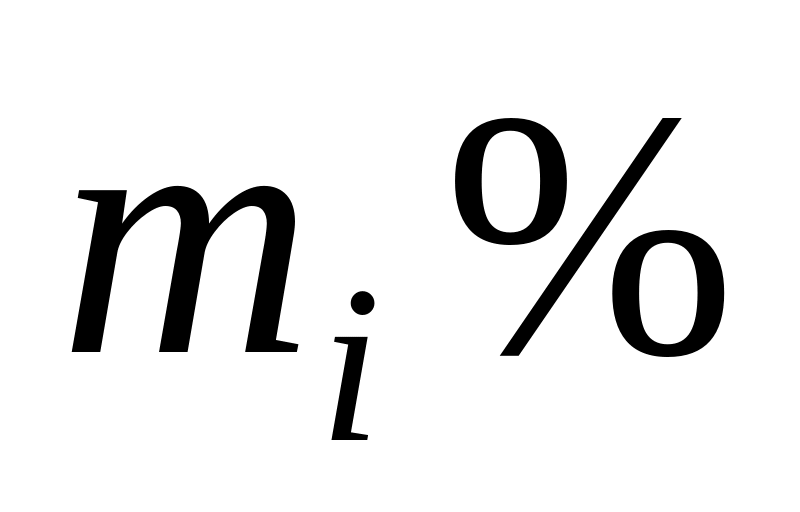виробів (
).
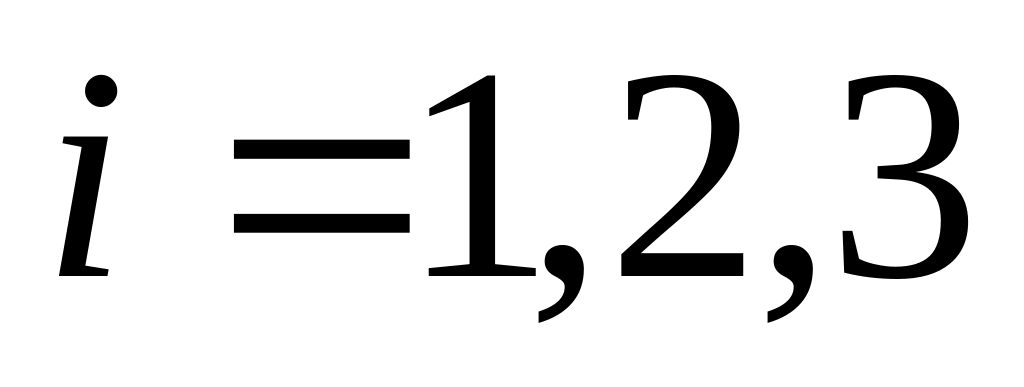Серед виробів
-го
заводу
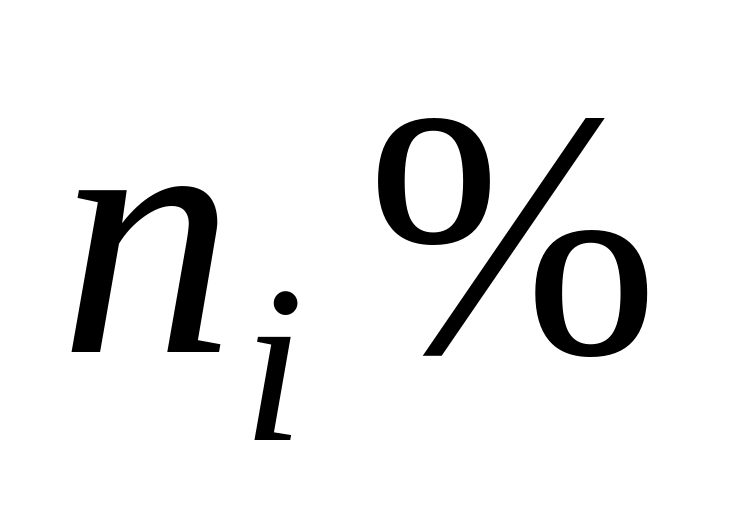якісних. Куплено один виріб. Він виявився
якісним.
Визначити
ймовірність того, що куплений виріб
виготовлено
-им
заводом.
Задачу розв'язати за даними таблиці ( ― номер варіанта ):
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
50 |
50 |
30 |
60 |
40 |
70 |
60 |
50 |
20 |
10 |
30 |
70 |
60 |
20 |
|
30 |
20 |
50 |
20 |
30 |
20 |
10 |
30 |
40 |
50 |
40 |
10 |
30 |
70 |
|
20 |
30 |
20 |
20 |
30 |
10 |
30 |
20 |
40 |
40 |
30 |
20 |
10 |
10 |
|
70 |
80 |
70 |
70 |
80 |
70 |
80 |
90 |
90 |
70 |
90 |
70 |
80 |
80 |
|
80 |
70 |
80 |
80 |
80 |
80 |
90 |
80 |
70 |
90 |
80 |
90 |
80 |
70 |
|
90 |
90 |
90 |
90 |
90 |
90 |
80 |
90 |
80 |
80 |
90 |
80 |
90 |
90 |
|
1 |
2 |
3 |
1 |
1 |
2 |
1 |
2 |
3 |
1 |
3 |
2 |
1 |
2 |
|
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
|
40 |
30 |
20 |
50 |
60 |
80 |
60 |
50 |
40 |
10 |
40 |
60 |
40 |
20 |
|
30 |
40 |
50 |
30 |
30 |
10 |
30 |
30 |
20 |
50 |
30 |
20 |
40 |
60 |
|
30 |
30 |
30 |
20 |
10 |
10 |
10 |
20 |
40 |
40 |
30 |
20 |
20 |
20 |
|
60 |
70 |
60 |
70 |
70 |
70 |
60 |
70 |
80 |
60 |
60 |
70 |
60 |
7 0 |
|
70 |
60 |
70 |
60 |
80 |
80 |
70 |
80 |
70 |
60 |
70 |
70 |
80 |
70 |
|
90 |
50 |
90 |
80 |
60 |
90 |
80 |
60 |
60 |
80 |
90 |
90 |
70 |
90 |
|
2 |
2 |
3 |
3 |
1 |
1 |
2 |
1 |
3 |
3 |
3 |
2 |
1 |
1 |
4.
Внаслідок маркетингових досліджень
встановлено, що ймовірність реалізації
одиниці продукції складає
.
Знайти ймовірність, що з
вироблених одиниць продукції буде
реалізовано: а) рівно
;
б) не більше
з
;
в) від
до
;
г) обчислити найімовірніше число
реалізованих одиниць.
Задачу розв'язати за даними таблиці ( ― номер варіанта ):
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
0,7 |
0,5 |
0,5 |
0,65 |
0,5 |
0,4 |
0,95 |
0,7 |
0,19 |
0,75 |
|
8 |
400 |
40 |
500 |
8 |
10 |
400 |
80 |
100 |
50 |
|
5 |
38 |
38 |
400 |
4 |
5 |
360 |
56 |
19 |
8 |
|
80 |
60 |
60 |
80 |
80 |
80 |
60 |
85 |
45 |
10 |
|
1 |
200 |
20 |
400 |
0 |
0 |
0 |
0 |
80 |
10 |
|
4 |
400 |
40 |
500 |
4 |
4 |
320 |
12 |
100 |
40 |
|
||||||||||
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
0,7 |
0,6 |
0,5 |
0,65 |
0,45 |
0,35 |
0,75 |
0,65 |
0,4 |
0,6 |
|
90 |
60 |
80 |
170 |
100 |
80 |
150 |
200 |
180 |
40 |
|
30 |
50 |
40 |
70 |
40 |
30 |
50 |
80 |
100 |
30 |
|
80 |
60 |
60 |
80 |
70 |
60 |
45 |
65 |
75 |
60 |
|
10 |
20 |
30 |
40 |
15 |
20 |
0 |
20 |
30 |
0 |
|
40 |
40 |
60 |
50 |
30 |
30 |
40 |
40 |
50 |
20 |
|
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
|
0,6 |
0,5 |
0,4 |
0,5 5 |
0,55 |
0,45 |
0,6 5 |
0,75 |
|
60 |
50 |
70 |
150 |
120 |
70 |
160 |
100 |
|
20 |
40 |
40 |
60 |
50 |
30 |
60 |
80 |
|
70 |
70 |
80 |
50 |
70 |
60 |
55 |
80 |
|
10 |
30 |
30 |
20 |
10 |
20 |
0 |
20 |
|
30 |
40 |
50 |
50 |
30 |
40 |
40 |
50 |
5. Ймовірність виконання договору для кожного з заводів дорівнює . Скласти закон розподілу числа заводів, які виконають договір.
Задачу розв'язати за даними таблиці ( ― номер варіанта ):
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
3 |
5 |
2 |
6 |
4 |
4 |
3 |
5 |
5 |
4 |
4 |
5 |
3 |
4 |
|
0,8 |
0,7 |
0,8 |
0,7 |
0,6 |
0,8 |
0,6 |
0,8 |
0,6 |
0,7 |
0,6 |
0,9 |
0,9 |
0,5 |
N |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
|
4 |
6 |
3 |
3 |
2 |
3 |
3 |
4 |
6 |
3 |
5 |
4 |
4 |
3 |
|
0,6 |
0,6 |
0,7 |
0,9 |
0,7 |
0,6 |
0,7 |
0,6 |
0,8 |
0,8 |
0,8 |
0,7 |
0,9 |
0,6 |
6.
Випадкова величина
задається функцією розподілу
.
Потрібно визначити: а) математичне
сподівання та середнє квадратичне
відхилення випадкової величини
;б)
ймовірність, що випадкова величина
прийме значення з інтервалу
.
де
―
номер варіанта,
.
7.
Задана генеральна сукупність. Зробити
вибірку з 20 елементів, починаючи з номера
.
Потрібно:
а)
побудувати статистичний розподіл
вибірки та його емпіричну функцію
;
б) обчислити числові характеристики вибірки;
в) побудувати полігон частот та гістограму, розбивши інтервал на 5 рівних підінтервалів;
г) знайти моду, медіану, розмах та коефіцієнт варіації.
Генеральна сукупність: 11, 13, 15, 16, 12, 13, 14, 15, 15, 12, 9, 11, 16, 10,12, 11, 10, 14, 15, 15, 16, 9, 16, 12, 13, 9, 10, 12, 15, 16, 17, 10,11, 12, 12, 13, 13, 15, 12, 12, 9, 9, 17, 17, 10, 10, 13, 14, 15, 16, 17, 17, 11, 11, 15, 15, 12, 5, 5, 5, 8, 8, 9, 10, 15, 15, 8, 11, 12, 16, 17, 9, 10, 12, 14, 14, 14, 17, 19, 19, 20, 19, 19, 17, 8, 8, 6, 6, 6, 15, 15, 12, 12, 13, 16, 16, 18, 14, 14, 9, 10.
8.
Знайти вибіркове рівняння прямої
регресії
на
за даними кореляційної таблиці (
―
номер варіанта).
|
|
|
|
|
|
|
― |
|
― |
|
― |
|
|
― |
|
― |
|
|
|
|
― |
|
― |
|
|
― |
― |
― |
|
|
|
|
|
|
|
|
|
― |
― |
|
― |
― |
|
― |
― |
|
|
― |
|
|
|
|
|
|
|
