§5. Порівняння двох середніх генеральних сукупностей,
дисперсії яких відомі (великі незалежні вибірки)
Нехай
і
об’єми великих
незалежних вибірок, для яких знайдені
відповідні вибіркові середні
та
.
Генеральні дисперсії
,
відомі.
Правило 1.
Для того, щоб при заданому рівні значимості
перевірити нульову гіпотезу
про рівність математичних сподівань
(генеральних середніх) двох нормальних
генеральних сукупностей з відомими
дисперсіями (у випадку великих вибірок)
при конкуруючій гіпотезі
,
потрібно порахувати спостережуване
значення критерію
,
і
по таблиці 2 функції Лапласа знайти
критичну точку
з рівності
.
Якщо
- нема підстави відкидати нульову
гіпотезу. Якщо
- нульова гіпотеза відкидається.
Правило 2.
При конкуруючій гіпотезі
знаходять критичну точку
по таблиці 2 з рівності
.
Якщо
- нема підстави відкидати нульову
гіпотезу, якщо ж
- нульова гіпотеза відкидається.
Правило 3.
При конкуруючій гіпотезі
знаходять точку
за правилом 2. Якщо
- нульова гіпотеза приймається, а якщо
- нульова гіпотеза відкидається.
Приклад 1. За двома
незалежними вибірками, об’єми яких
,
вибраних з нормальних генеральних
сукупностей, знайдемо
і
.
Генеральні дисперсії відомі:
,
.
Потрібно при рівні значимості
перевірити нульову гіпотезу
при
.
Рішення.
Знайдемо
.
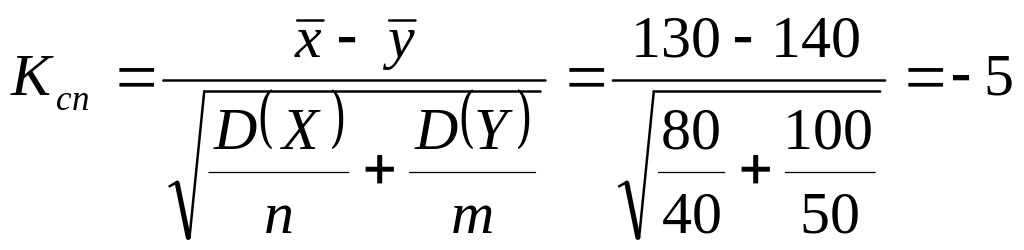Так як
,
то критична область двостороння. Знайдемо
з рівності
, тобто згідно табл.2
.
Так як
, то нульова гіпотеза відкидається,
тобто генеральні середні різніться
суттєво.
Лекція 10. КОРЕЛЯЦІЙНИЙ І РЕГРЕСІЙНИЙ АНАЛІЗ
В багатьох задачах потрібно встановити залежність випадкової величини Y від однієї чи декількох інших величин. Залежності між величинами можна поділити на функціональні і статистичні. В природничих, технічних науках здебільшого зустрічаються функціональні залежності, при яких кожному значенню аргументу х за певним законом відповідає зазвичай одне значення функції y.
Строга функціональна залежність здійснюється рідко, так як обидві величини х та y, чи одна з них підпадає під дію випадкових впливів (факторів), причому деякі з них можуть бути спільними для обох величин х та y.
Між змінними, що характеризують економічні величини, здебільшого існують залежності, які проявляються в тому, що одна з них реагує на зміну іншої зміною свого закону розподілу. Наприклад, урожайність сільськогосподарських культур залежить від кількості внесеного добрива, але ця залежність не буде функціональна, оскільки на врожайність, крім того, впливатимуть кліматичні умови, технологія землі та посіву тощо.
Статистичною називають залежність, при якій зміна однієї з величин веде до зміни розподілу іншої, зокрема кореляційним називається зв’язок між статистичними змінними Х і Y, за якими при зміні ознаки Х змінюється середнє значення ознаки Y. Причому при кореляційній залежності одному значенню незалежної змінної Х відповідає не одна, а декілька значень залежної змінної Y. Наведений приклад показує, що середня врожайність є функцією від кількості внесеного добрива, тобто Y зв’язаний з Х кореляційною залежністю.
Отже, дві випадкові величини X і Y не є незалежними, то вони називаються залежними випадковими величинами. При цьому залежність між величинами Х і Y не є, взагалі кажучи, функціональною і носить ймовірносний (стохастичний) характер. Така ймовірність вивчається методами теорії ймовірності і математичної статистики. Вивченню статистичної залежності випадкових величин і присвячений цей розділ.