§4. Перевірка гіпотези про нормальний закон розподілу генеральної сукупності. Критерій узгодженості Пірсона

В попередніх параграфах закон розподілу генеральної сукупності припускається відомим. Якщо ж він є невідомим, але є підстава, припущення, що він має певний вигляд (наприклад А), то перевіряють нульову гіпотезу: генеральна сукупність розподілена по закону А.

Перевірка гіпотези про припущений закон невідомого закону розподілу робиться так само, як і перевірка гіпотези про параметри розподілу, тобто з допомогою спеціально підібраної випадкової величини – критерію узгодженості.

Критерієм узгодженості називають критерій перевірки про вигляд невідомого розподілу.

Є декілька критеріїв узгодженості: (хі квадрат) Пірсона, Колмогорова, Смірнова і т.д. Для простоти обмежимося лише описом застосування критерію Пірсона для перевірки гіпотез про нормальний розподіл генеральної сукупності, оскільки інші закони перевіряються аналогічно.

Для перевірки критерію узгодженості за конкретними формулами порівнюють емпіричні частоти (за даними вибірки) n_і і теоретичні n_i' (обчислені в припущенні, що закон розподілу генеральної сукупності заданий, наприклад, у нашому випадку - нормальний).

Природно, що емпіричні та теоретичні частоти різняться, але чи випадкова ця розбіжність? Можливо, що розбіжність випадкова (незначна), а можливо, розбіжність невипадкова, і пояснюється це тим, що теоретичні частоти обчислені, виходячи з неправильної гіпотези про нормальний розподіл генеральної сукупності.

Критерій Пірсона якраз і відповідає на поставлене питання, правда, як і всякий критерій, він не доводить справедливість гіпотези, а лише встановлює на певному рівні значимості її узгодження чи неузгодження з даними спостереженнями.

Найбільш розповсюдженим критерієм перевірки нульової гіпотези про закон розподілу ознаки генеральної сукупності є критерій узгодженості , що розраховується за формулою:

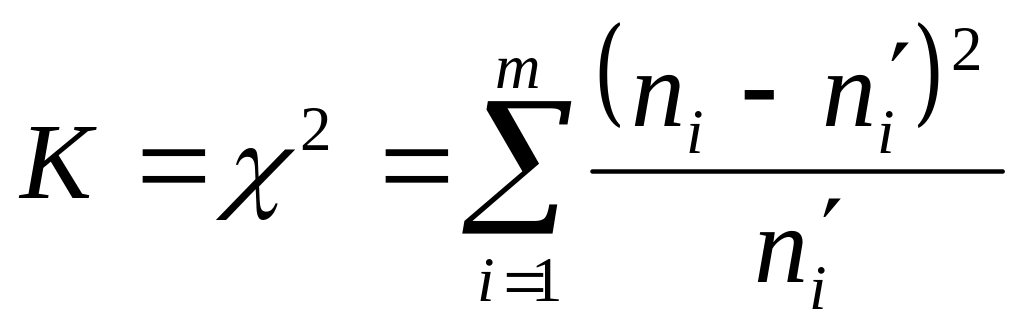, (1)

де m – число часткових інтервалів, на які поділяється статистичний розподіл вибірки; n_i – частота ознаки в і-му інтервалі; n_i' – теоретичні частоти, підраховані за відповідними формулами закону розподілу ймовірностей, який припускається для ознаки генеральної сукупності. Теоретичні частоти знаходяться за формулою:

, (2)

де n – об’єм вибірки, р_і – для дискретної величини є ймовірність події р_і=Р(Х=х_і), для неперервної випадкової величини р_і є ймовірність того, що ознака Х попаде в і-ий інтервал.

Наприклад, для гіпотези H₀, яка припускає, що ознака генеральної сукупності має нормальний закон розподілу, ймовірність р_і може бути обчислена за формулою:

Р_і=Ф(х_і+1)-Ф(х_і), (3)

де Ф(х) – функція Лапласа.

Критерій К у формулі (1) випадковий, і чим менше відрізняються значення емпіричних і теоретичних частот, тим менше буде значення К_сп і, отже, більш точно характеризує близькість теоретичного і емпіричного розподілів.

Значення критичної точки k_кр для критерію узгодженості Пірсона залежить від рівня значимості і числа ступенів вільності k. Число ступенів вільності розподілу визначається за формулою k=l-r-1, де l- число інтервалів статистичного ряду, r – число параметрів теоретичного закону розподілу, що оцінюється за даними вибірки.

Зокрема , якщо припущений розподіл нормальний, то оцінюється два параметри (математичне сподівання і середнє квадратичне відхилення), тому r=2, отже, k=l-3.

Оскільки односторонній критерій більш “жорстко” відхиляє нульову гіпотезу, ніж двосторонній, то будуть правосторонню критичну область, виходячи з вимоги, щоб ймовірність попадання критерію в цю область при припущенні правдивості нульової гіпотези була рівна прийнятому рівню значимості :

.

Висновок. Для того, щоб при заданому рівні значимості перевірити гіпотезу Н₀: генеральна сукупність розподілена нормально, потрібно спочатку порахувати теоретичні частоти, а потім спостережуваний критерій:

.

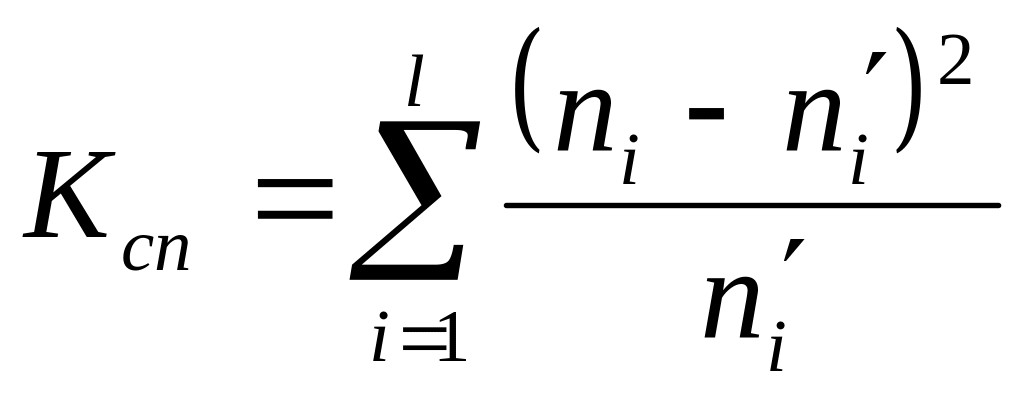Після чого по таблиці критичних точок розподілу (див. дод.1), за заданим рівнем значимості і числом ступенів вільності k=l-3 потрібно знайти критичну точку .

Якщо К_сп<k_кр – нема підстави відхиляти нульову гіпотезу.

Якщо К_сп>k_кр – нульову гіпотезу відхиляють.

Зауваження. Об’єм вибірки повинен бути досить великим (не менше 50), а кожна група з інтервалу (х_і,х_і+1) містити не менше 5-8 варіант; малочисленні групи слід об’єднувати в одну, сумуючи частоти.

Для контролю обчислень, формулу (1) перетворюють до вигляду:

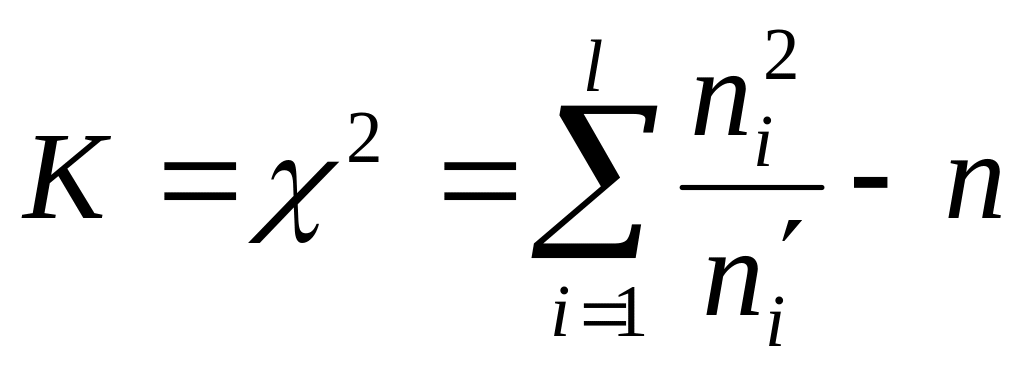
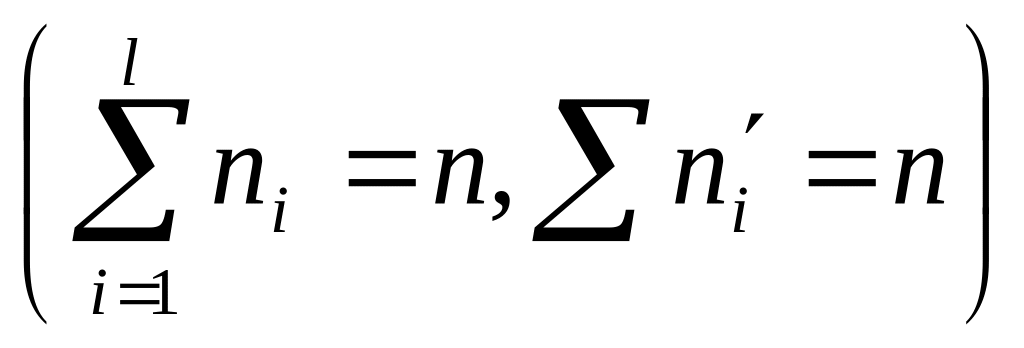
Отже, суть критерію узгодженості Пірсона полягає в порівнянні емпіричних і теоретичних частот. Емпіричні частоти знаходять експериментально, а теоретичні, наприклад, таким методом:

1. Весь інтервал спостережуваних значень Х (вибірки об’єму n) ділять на l часткових інтервалів [x_i,x_i+1] однакової довжини. Знаходять їх середини , а частоти n_i варіанти беремо рівними числу варіант, що попали в і-ий інтервал.

В результаті отримано послідовність рівновіддалених варіант з відповідними частотами:

.

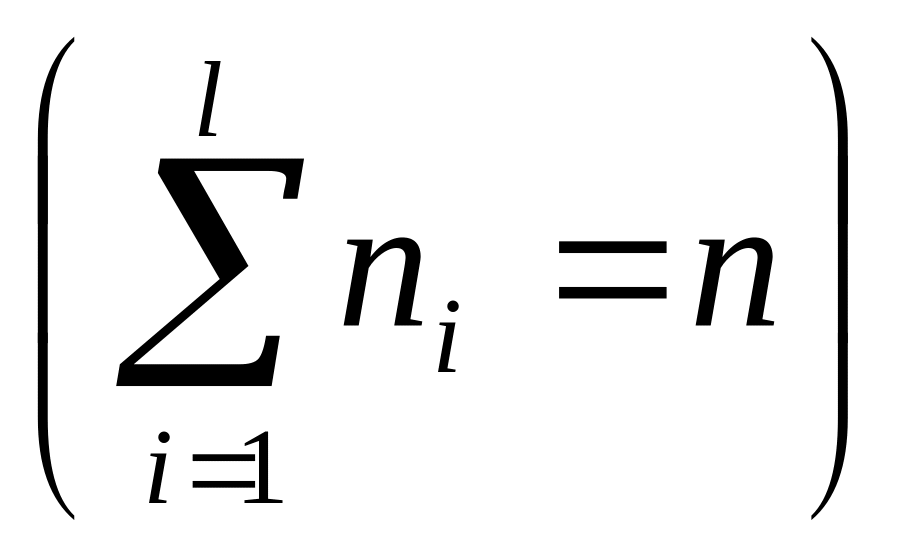
2. Обчислюємо вибіркову середню і вибіркове середнє квадратичне відхилення:

.

3. Нормують випадкову величину Х, тобто переходять до величини і обчислюють кінці інтервалів (z_i,z_i+1):

,

причому найменше значення Z, тобто z₁ покладають рівним , а найбільше, тобто z_e, рівним .

4. Обчислюють теоретичні ймовірності р_і попадання Х в інтервали (х_і,х_і+1) з рівності

Р_і=Ф(z_і+1)-Ф(z_і),

де Ф(z) – функція Лапласа і остаточно знаходять теоретичні частоти n_i'=np_i.

Приклад 1. Вивчається відсоткове відношення номінальної і ринкової цін на акції на фондовому ринку (Х) за певний період. Зроблена вибірка за акціями 50-ти різних підприємств.

98,01	100,02	98,1	96,2	99,8
101,2	99,2	104,1	102,6	103,8
101,2	99,4	104,1	100,6	99,8
97,2	98,2	101,1	100,6	99,8
100,8	98,2	100,1	101,6	96,1
101,2	97,2	102,1	96,3	96,8
98,8	97,2	102,0	96,3	98,8
99,2	100,3	100,1	99,6	100,8
100,5	98,2	103,5	100,1	98,8
100,4	97,2	102,1	101,6	100,8

Потрібно за допомогою критерію узгодження Пірсона перевірити гіпотезу про нормальний закон розподілу відсоткового відношення номінальної і ринкової цін на акції на фондовому ринку при рівні значимості .

Рішення. І. Min x_i=96,1%, max x_i=104,1%, тому побудуємо інтервальний статистичний ряд відсотків від 94,1% до 104,1%. Розмах варіації для даного ряду становить R=104,1-96,1=8%, тому поділимо інтервальний ряд на 8 частин.

96,1 97,1

97,1 98,1

98,1 99,1

99,1 100,1

100,1 101,1

101,1 102,1

102,1 103,1

103,1 104,1

Будуємо статистичний розподіл, варіантами якого є середини інтервалів:

	96,6	97,6	98,6	99,6	100,6	101,6	102,6	103,6
ni	5	6	6	12	9	9	1	2

Для знаходження теоретичних частот n_i використаємо формули:

і скористаємось розрахунковою таблицею.

№	Межі інтер-валів
1	96,1 - 97,1		-∞	-1,400	-0,5	-0,4152	0,085	5	4,25
2	97,1 – 98,1		-1,400	-0,860	-0,4125	-0,3051	0,110	6	5,50
3	98,1 – 99,1		-0,860	-0,322	-0,3051	-0,1255	0,180	6	9,00
4	99,1 – 100,1		-0,322	0,215	-0,1255	0,0852	0,211	12	10,54
5	100,1 – 101,1		0,215	0,753	0,0852	-0,2734	0,188	9	9,40
6	101,1 – 102,1		0,753	1,290	0,2734	0,4015	0,128	9	6,40
7	102,1 – 103,1		1,290	1,828	0,4015	0,4664	0,065	1	3,25
8	103,1 – 104,1		1,828		0,4664	0,5	0,025	2	1,25

Значення критерію К_сп обчислюється за формулою:

.

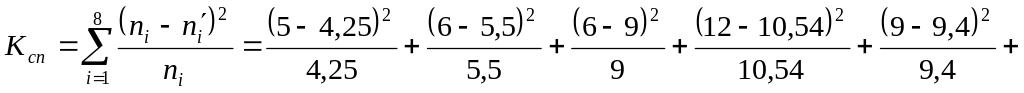
За таблицями критичних точок розподілу .

Оскільки К_сп=4,46<11,1=k_кр, то гіпотеза про нормальний закон розподілу відсоткового відношення номінальної і ринкової цін на акції на фондовому ринку приймається.