Лекція 8. Статистичні оцінки параметрів генеральної сукупності

§1. Точкові статистичні оцінки параметрів

Розглянемо наступну загальну задачу. Маємо випадкову величину х, закон розподілу якої має невідомий параметр а. Потрібно на основі даних вибірки знайти добру оцінку параметру а.

Нехай а^* - статистична оцінка невідомого параметру а теоретичного розподілу (генеральної сукупності). Припустимо, що по вибірці об’єму n знайдена оцінка .

Повторимо експеримент, тобто візьмемо знову вибірку об’єму n з генеральної сукупності і по ній знайдемо оцінку і т.д. Таким чином оцінку а^* можна розглядати як випадкову величину, що має закон розподілу, який залежить, по-перше, від закону розподілу випадкової величини Х, по-друге, від числа експериментів n, а числа - як її можливі значення.

Припустимо, що оцінка а^* дає наближене значення а з надлишком; тоді кожне знайдене за даними вибірок число більше істинного значення а. Зрозуміло, що в цьому випадку і математичне сподівання (середнє значення) випадкової величини а^* більше, ніж а, тобто M[a^*]>a. Теж саме, очевидно, якщо а^* дає оцінку з недостачею, то M[a^*]<a.

Таким чином, використання статистичної оцінки, математичне сподівання якої не рівне оцінюючому параметру, привело б до систематичних (одного знаку) похибок. Тому потрібно вимагати, щоб математичне сподівання оцінки було рівне шуканому параметру. Хоча дотримання цієї вимоги не усуне похибку, проте похибки різних знаків будуть взаємно компенсуватись. Тобто дотримання умови M[a^*]=a гарантує відсутність систематичних похибок.

Незміщеною називають статистичну оцінку а^*, математичне сподівання якої дорівнює параметру, що оцінюється при будь-якому об’ємі вибірки, тобто

M[a^*]=a. (1)

Зміщеною будемо називати статистичну оцінку, для якої порушується умова (1), тобто .

Проте помилково було б вважати, що незміщена оцінка завжди дає добрі наближення оціненого параметру. Справа в тому, що можливі значення а^* можуть бути сильно розсіяні навколо свого середнього значення. Наприклад, може виявитися дуже віддалено від середнього значення , а значить, і від самого параметру а; прийнявши за наближене значення а, ми допустилися б грубої похибки. Отже, необхідно вимагати, щоб дисперсія а^* була малою. По цій причині до статистичної оцінки ставиться вимога ефективності.

Ефективною називається статистична оцінка, яка при заданому обсязі вибірки n має найменшу дисперсію.

При вибірці великого обсягу (n велике) до статистичних оцінок ставляться вимоги змістовності.

Змістовною (спроможною) називають статистичну оцінку, яка при прямує за ймовірністю до параметру, що оцінюється:

. (2)

Для виконання вимоги (2) досить, щоб дисперсія оцінки прямувала до нуля, коли , тобто, щоб виконувалась умова

, (3)

і, крім того, щоб оцінка була незміщеною. Від формули (2) легко перейти до виразу (3), якщо скористатись нерівністю Чебишева.

Прикладом змістовної оцінки можуть слугувати закони великих чисел, наприклад, теорема Бернуллі. Очевидно, такій умові повинна задовольняти всяка оцінка, придатна для практичного використання.

Як уже згадувалось, для генеральної сукупності, заданої розподілом (для простоти обмежимось випадком дискретної випадкової величини):

xi	x1	x2	…	xk
Ni	N1	N2	…	Nk

середня генеральна розраховується за формулою

.

Аналогічна формула справедлива і для вибірки

.

Але зауважимо, що вибіркова середня, знайдена за даними вибірки є певним (випадковим) числом. При інших вибірках з тієї ж генеральної сукупності, середня вибіркова, взагалі кажучи, змінює свої значення, тобто характеристику можна розглядати як випадкову величину і тому говорити про її розподіл (теоретичний чи емпіричний), а також про числові характеристики цього розподілу, зокрема, про числа та .

Крім того, в теоретичних міркуваннях значення вибірки x₁,x₂,…x_k випадкової величини Х, одержані в результаті незалежних випробувань, розглядаються як випадкові величини X₁,X₂,…X_k, що мають ті ж числові характеристики і той же розподіл, що й Х. Звідси, як для однаково розподілених випадкових величин .

З іншої сторони, як для однаково розподілених випадкових величин

.

Тобто ,а це свідчить, що вибіркова середня є незміщеною оцінкою генеральної середньої.

Якщо допустити, що вибіркові величини Х₁,...Х_k мають обмежені дисперсії, то за теоремою Чебишева для однаково розподілених випадкових величин

для довільного , а це вказує на те, що оцінка для є також і змістовною. Отже, при збільшенні об’єму вибірки n вибіркова середня прямує до . В цьому і полягає властивість стійкості вибіркових середніх.

Дисперсії розраховуються за формулами :

.

Перетворимо вирази до вигляду:

, (1)

, (2)

де .

Перший доданок рівності (1) збігається за ймовірністю до , а другий до , тобто вся права частина до правої частини рівності (2), значить, статистична дисперсія D_r є змістовною оцінкою дисперсії D_В.

Якщо ж в ролі оцінки генеральної дисперсії взяти вибіркову дисперсію, то ця оцінка буде приводити до системних похибок (одного знаку, бо ), даючи занижене значення генеральної дисперсії. Отже, вибіркова дисперсія є зміщеною оцінкою генеральної дисперсії, тобто математичне сподівання вибіркової дисперсії не рівне генеральній дисперсії, а рівне:

. (3)

Легко “виправити” вибіркову дисперсію так, щоб її математичне сподівання було рівне генеральній дисперсії. Для цього досить помножити D_В на , тим самим отримавши виправлену дисперсію, яку звичайно позначають через S²:

. (4)

Виправлена дисперсія є незміщеною оцінкою генеральної дисперсії. Дійсно,

.

Зауважимо, що і “виправлене” середнє квадратичне відхилення:

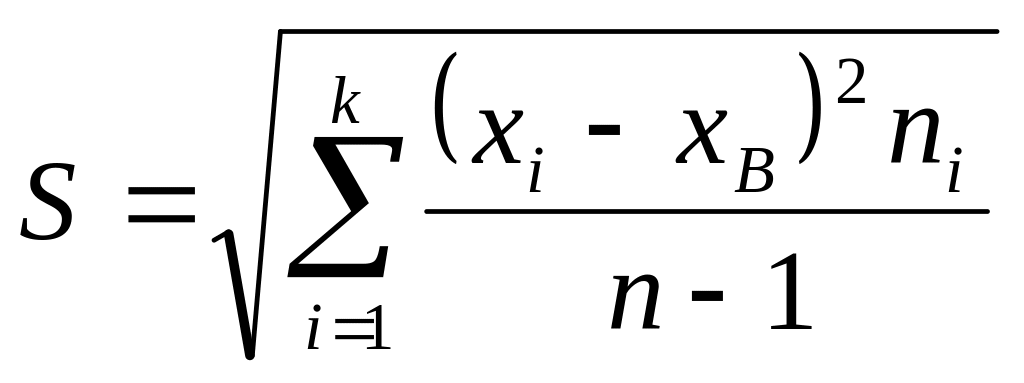. (5)

є незміщеною оцінкою. Крім того, при великих об’ємах вибіркова і виправлена дисперсії відрізняються мало. На практиці користуються виправленою дисперсію приблизно при n<30. У цьому випадку значення множника , що стоїть перед D_В є більшим за число .

Приклад. З булочок, що їх випікає хлібозавод, зроблено вибірку. Зважування булочок, що попали у вибірку, дало такі результати (в грамах):

100,3 101,2 99,6 102,4 100,3 100,4

102,7 98,6 101,2 98,3 99,5 101,2

100,7 99,8 100,7 100,6 99,2 99,7

100,4 101,1 100,1 100,7 99,3 98,9

100,2 98,8 98,9 98,2 97,6

99,2 98,3 99,7 101,3 98,7

99,7 101,6 103,2 99,4 101,5

Знайти:

Рішення. Результати вибірки та їх обчислення зводимо в таблицю:

№ п/п	Інтервал xi-1<X<xi		ni
1	97-97,5	97,25	1	194,5	37830,25	194,5	37830,25
2	97,5-98,0	97,75	1	195,5	38220,25	195,5	38220,25
3	98,0-98,5	98,25	3	196,5	38612,25	589,5	38612,25
4	98,5-99,0	98,75	4	197,5	39006,25	790	156025
5	99,0-99,5	99,25	5	198,5	39402,25	992,5	197011,25
6	99,5-100,0	99,75	6	199,5	39800,25	1197	238801,5
7	100,0-100,5	100,25	7	200,5	40200,25	1403,5	281401,75
8	100,5-101,0	100,75	4	201,5	40602,25	806	162409
9	101,0-101,5	101,25	4	202,5	41006,25	810	164025
10	101,5-102,0	101,75	2	203,5	41412,25	402	82824,5
11	102,0-102,5	102,25	1	204,5	41820,25	204,5	211820,75
12	102,5-103,0	102,75	1	205,4	42230,25	205,5	42290,25
13	103,0-103,5	103,25	1	206,5	42642,25	200,5	42642,25
	n=0,5	100,25	40			8002	40026949

;

.

Для знаходження М_о будемо користуватись формулою:

, (6)

де x_r – ліва межа модального інтервалу, n_r –частота модального інтервалу; n_r-1, n_r+1 – частоти відповідного попереднього і наступного інтервалів; h- ширина модального інтервалу. В нашому прикладі: x_r=100,0, n_r=7, n_r-1=6, n_r+1=4, h=0,5. А тому

.

Для знаходження Ме припускаємо рівномірний розподіл ознаки в медіанному інтервалі, тому

. (7)

Маємо: x_r=99,5; n_r=6, n_r+1=14 , h=0,5;

.