§2. Теорема Чебишева

Означення. Послідовність випадкових величин Х₁, Х₂, ...Х_n,... збігається по ймовірності до величини а, якщо для довільного

.

Теорема Чебишева. Якщо Х₁, Х₂, ...Х_n, ... попарно незалежні випадкові величини, що мають рівномірно обмежені дисперсії , то для будь-якого малого числа , ймовірність нерівності

буде як завгодно близька до одиниці, якщо число випадкових величин достатньо велике, тобто

.

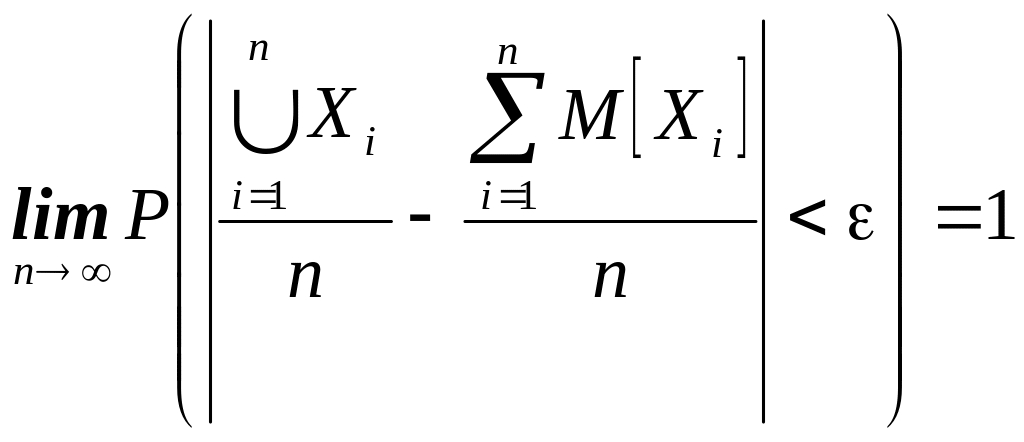Отже, теорема Чебишева стверджує, що коли розглянути досить велике число незалежних випадкових величин, що мають обмежені дисперсії, то майже достовірною є подія, що відхилення середнього арифметичного випадкових величин від їх математичного сподівання буде по абсолютній величині як завгодно малим числом.

Доведення. Розглянемо випадкову величину 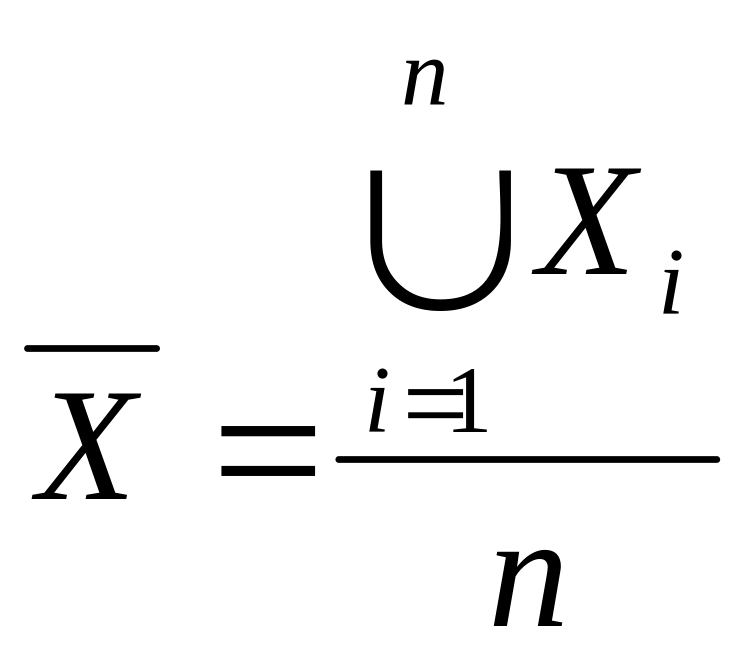і знайдемо її числові характеристики:

(при умові ).

Застосуємо нерівність Чебишева до випадкової величини :

.

Яке б не було мале , то при , величина , тобто

.

Теорема Чебишева має практичне застосування в теорії похибок, коли за істинне значення деякої величини беруть середнє арифметичне даних, отриманих в експериментах, що проводяться в однакових умовах. В математичній статистиці по теоремі Чебишева побудований вибірковий метод, суть якого полягає в тому, що про поведінку всієї сукупності можна судити за даними невеликої випадкової вибірки.

Приклад 1. Ймовірність, що холодильник витримає гарантійний термін роботи, дорівнює 0.8 для всіх 100 холодильників, які обслуговує гарантійна майстерня. Оцінити ймовірність, що число холодильників, які витримають гарантійний термін роботи, буде в межах [75;85].

Рішення. Випадкова величина Х – число холодильників, що витримають гарантійний термін роботи, розподілена за біноміальним законом, тому , , .

Використаємо нерівність Чебишева:

.

§3. Теорема Бернуллі

Частковим випадком теореми Чебишева є теорема Бернуллі. Ця теорема вважається початком теорії ймовірності як науки.

Теорема Бернуллі. Нехай у кожному із n незалежних випробувань ймовірність появи події А є постійно р. Тоді

,

де - відносна частота події А.

Доведення. Нехай випадкова величина Х₁ – число появи події А в першому випробуванні, Х₂ – число появи події А в другому випробуванні і т.д. Тоді кожна з величин Х_і має розподіл:

Хі	0	1
Рі	q	p

де q=1-p.

Тоді: , ,

.

Застосуємо теорему Чебишева

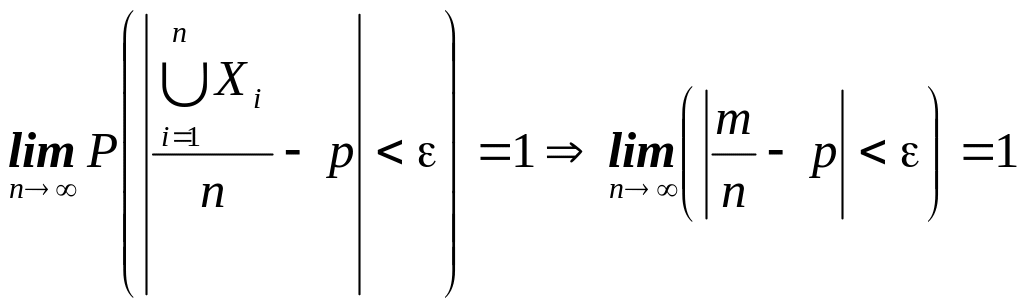
для будь-якого числа .

§4. Центральна гранична теорема Ляпунова

Розглянуті в попередніх параграфах теореми є різними формами закону великих чисел і встановлюють факти збіжності по ймовірності деяких випадкових величин до їх постійних характеристик. При цьому ні в одній з них ми не мали справу з законами розподілу випадкових величин.

В цьому параграфі ми розглянемо питання, зв’язане з знаходженням граничного закону розподілу об’єднання

,

коли число складових необмежено зростає. Центральна гранична теорема теорії ймовірності (теорема Ляпунова) встановлює умови, при яких вказаний граничний закон є нормальним.

Сформулюємо просту форму центральної граничної теореми, коли випадкові величини Х₁, Х₂, ...Х_n,... взаємно незалежні.

Теорема. Якщо випадкова величина є об’єднанням великого числа взаємно незалежних величин, вплив кожної з яких на всю суму є дуже незначним, то Y має розподіл, близький до нормального.

Ця теорема дає одну з можливих відповідей на питання, чому нормально розподілені випадкові величини часто зустрічаються на практиці.

Приклад 1. Кожна зі 100 незалежних випадкових величин розподілена за показниковим законом розподілу з параметром . Побудувати наближений закон розподілу випадкової величини .

Рішення. Оскільки значення густини показникового закону розподілу для x>0 і - число мале порівняно зі всією сумою, то його вплив на Y незначний. Тоді по теоремі Ляпунова Y буде розподілена за законом, близьким до нормального.

За умовою ; , а тому

, .

Густина розподілу має вигляд: , .

Приклад 2. Кожна з 24 незалежних випадкових величин розподілена за рівномірним законом на інтервалі (0,1). Записати наближений вигляд для густини об’єднання цих випадкових величин. Знайти ймовірність того, що сума буде в межах від 6 до 8.

Рішення. За теоремою Ляпунова випадкова величина буде мати розподіл близький до нормального. Порахуємо , , , .

Отже, густина розподілу , тому:

.

Лекція 7. ПРЕДМЕТ МАТЕМАТИЧНОЇ СТАТИСТИКИ.

ГЕНЕРАЛЬНА СУКУПНІСТЬ І ВИБІРКА

Математичною статистикою називається наука, що займається розробкою методів отримання, опису і обробки експериментальних даних з метою вивчення закономірностей випадкових масових явищ.

Всі задачі математичної статистики умовно можна розчленити на дві групи.

Першою з них є розробка методів збору і групування статистичних даних, отриманих в результаті спостережень, опрацювання статистичних звітів чи даних в результаті спеціально поставлених експериментів.

Друга задача полягає в розробці методів аналізу статистичних даних залежно від мети. Сюди належать:

а) оцінка ймовірності події; знаходження функції розподілу випадкової величини; оцінка залежності випадкової величини від інших випадкових величин, тощо; оцінка невідомих параметрів розподілу;

б) перевірка статистичних гіпотез про зроблені вище припущення.

Висновки за допомогою методів математичної статистики, зроблені зі зібраних статистичних даних, повинні правильно відображати загальні ймовірносні характеристики процесу, що досліджується.

Сучасна математична статистика розробляє способи визначення числа необхідних випробувань до початку дослідження (планування експерименту), а в ході досліджень вказує, як проводити послідовний аналіз даних. Тому, в деяких підручниках, її визначають як науку про прийняття рішень в умовах невизначеності.

Основними поняттями в математичній статистиці є генеральна та вибіркова сукупності. Нехай потрібно вивчити деяку ознаку, властиву великій множині однотипних виробів. Сукупність значень ознаки всіх виробів даного типу називається генеральною сукупністю. При цьому припускається, що число N в генеральній сукупності досить велике, навіть нескінченне.

На практиці проте суцільне обслідування застосовують досить рідко. Наприклад, якщо сукупність містить дуже велике число виробів, то провести суцільне обслідування фізично неможливо. Тим більше, якщо обслідування виробів зв’язане з їх знищенням (наприклад, фотоплівка), або вимагає великих матеріальних затрат, то проводити суцільне обслідування практично не має змісту. В таких випадках випадково вибирають зі всієї сукупності обмежене число об’єктів (виробів) й піддають їх обслідуванню.

Вибірковою сукупністю, або просто вибіркою, називають сукупність випадково відібраних n об’єктів з генеральної сукупності.

Число елементів генеральної сукупності N називають її обсягом (об’ємом), а число n – відповідно обсягом (об’ємом) вибірки, причому

.

Таким чином, вибірковий метод полягає в тому, що із генеральної сукупності береться вибірка і визначаються характеристики вибірки, котрі беруться в ролі наближених значень відповідних характеристик генеральної сукупності.

Чим більше n, тим більш обґрунтовано можна судити на основі вибірки про властивості генеральної сукупності. Очевидно, при вибірковий розподіл наближається до генерального. Відмітимо, що вибірка дає найбільшу інформацію про генеральну сукупність тільки в тому випадку, коли результати обслідування, що складають вибірку, є незалежними.