
- •2. Двойные интегралы в полярной системе координат.
- •3. Тройные интегралы, их свойства и вычисление в декартовых координатах.
- •4. Тройной интеграл в цилиндрической и сферической системах координат.
- •5. Приложения двойных и тройных интегралов.
- •6. Определение криволинейного интеграла 1-го рода, свойства, вычисление, применение.
- •7. Определение криволинейных интегралов 2-го рода, свойства, вычисление, применение.
- •8. Формула Грина.
- •9. Числовые ряды. Сходимость ряда и его сумма.
- •10. Необходимый признак сходимости. Гармонический ряд.
- •11. Достаточные признаки сходимости рядов с положительными членами: Даламбера, Коши, интегральный признак Коши, признаки сравнения.
- •12. Ряд Дирихле и его сходимость.
- •13. Знакочередующиеся ряды. Признак Лейбница.
- •14. Знакопеременные ряды. Абсолютная и условная сходимость.
- •15. Функциональные ряды. Основные понятия. Область сходимости.
- •16. Степенные ряды. Радиус и интервал сходимости. Теорема Абеля.
- •17. Разложение функций в степенные ряды. Ряды Тейлора и Маклорена.
- •18. Применение степенных рядов к приближенным вычислениям.
- •19. Элементы комбинаторики.
- •20. Основные понятия теории вероятностей.
- •21. Пространство элементарных событий. Алгебра событий.
- •22. Классическое и статистическое определение вероятности и ее свойства.
- •23. Теоремы сложения вероятностей.
- •24. Условная вероятность. Теоремы умножения вероятностей.
- •25. Формула полной вероятности. Формула Байеса.
- •26. Схема испытаний Бернулли. Формула Бернулли.
- •27. Предельные теоремы в схеме Бернулли: Пуассона, Муавра-Лапласа.
- •28. Наивероятнейшее число появлений события при повторных испытаниях по схеме Бернулли.
- •29. Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях.
- •30. Дискретные случайные величины и законы их распределения.
- •31. Непрерывные случайные величины и законы их распределения.
- •32. Функция распределения вероятностей св и ее свойства.
- •33. Дифференциальная функция распределения непрерывной св (плотность распределения св) и ее свойства.
- •34. Математическое ожидание св и ее свойства.
- •35. Дисперсия св и ее свойства. Среднее квадратическое отклонение.
- •36. Биномиальное распределение и его числовые характеристики.
- •37. Равномерное и показательное распределения, их числовые характеристики.
- •38. Нормальное распределение и его числовые характеристики.
31. Непрерывные случайные величины и законы их распределения.
СВ, возможные
значения которых заполняют целый
конечный или бесконечный промежуток
оси Ох – непрерывные СВ.
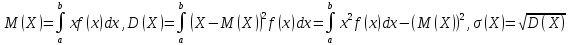 .
.
32. Функция распределения вероятностей св и ее свойства.
Функция
распределения – вероятность того, что
СВ Х примет значение, меньшее, чем
заданное х, т.е. F(x)=P(X<x).
Свойства – 1) F(x)
– вероятность, значит
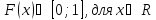 ;
2) Для любых х1 и х2 ϵ R,
связанных соотношением x1<x2,
F(x1)
;
2) Для любых х1 и х2 ϵ R,
связанных соотношением x1<x2,
F(x1)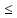 F(x2),
т.е. F(x) –
неубывающая функция; 3) Имеет место
равенство
F(x2),
т.е. F(x) –
неубывающая функция; 3) Имеет место
равенство
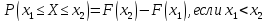 ;
4) F(x) всегда
непрерывна слева, т.е.
;
4) F(x) всегда
непрерывна слева, т.е.
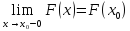 ;
5)
;
5)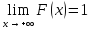 ,
,
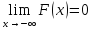 .
.
33. Дифференциальная функция распределения непрерывной св (плотность распределения св) и ее свойства.
НСВ можно
задать функцией, которую называют
плотностью вероятностей или дифференциальной
функцией распределения – функция
f(x)=F’(X).
Свойства – 1)
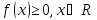 ,
F(X) неубывающая,
значит
,
F(X) неубывающая,
значит
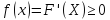 ;
2)
;
2)
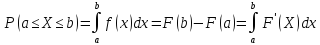 .
Геометрически, вероятность f(x)=F’(X)
= площади заштрихованной криволинейной
трапеции.
.
Геометрически, вероятность f(x)=F’(X)
= площади заштрихованной криволинейной
трапеции.
3) Если f(x)
– плотность вероятностей СВ Х, то
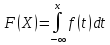 ;
4) Имеет место соотношение
;
4) Имеет место соотношение
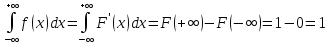 – условие нормировки. График плотности
распределения – кривая распределения
– 1) Всегда лежит в верхней координатной
полуплоскости; 2) Площадь, заключенная
между этой кривой и осью Ох=1
– условие нормировки. График плотности
распределения – кривая распределения
– 1) Всегда лежит в верхней координатной
полуплоскости; 2) Площадь, заключенная
между этой кривой и осью Ох=1
34. Математическое ожидание св и ее свойства.
Математическое
ожидание (среднее значение) ДСВ – сумма
всех произведений, значений СВ на
соответствующие им вероятности,
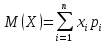 .
Свойства – 1) М(Х) постоянной величины
= самой постоянной, т.е. М(С)=С, С=const;
2) Постоянный множитель можно выносить
за знак МО, т.е. M(kX)=kM(X),
k=const; 3) М(Х) алгебраической суммы конечного
числа СВ = алгебраической сумме их М(Х),
т.е.
.
Свойства – 1) М(Х) постоянной величины
= самой постоянной, т.е. М(С)=С, С=const;
2) Постоянный множитель можно выносить
за знак МО, т.е. M(kX)=kM(X),
k=const; 3) М(Х) алгебраической суммы конечного
числа СВ = алгебраической сумме их М(Х),
т.е.
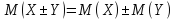 ;
4) М(Х) произведения независимых СВ =
произведению их М(Х), т.е. M(XY)=M(X)M(Y);
5) М(Х) отклонения СВ от ее М(Х) всегда =0,
т.е. М(Х-М(Х))=0. МО СВ характеризует ее в
среднем, центр ее распределения 2-ая
отличительная особенность СВ – степень
разброса значений этой величины по
отношению к ее центру.
;
4) М(Х) произведения независимых СВ =
произведению их М(Х), т.е. M(XY)=M(X)M(Y);
5) М(Х) отклонения СВ от ее М(Х) всегда =0,
т.е. М(Х-М(Х))=0. МО СВ характеризует ее в
среднем, центр ее распределения 2-ая
отличительная особенность СВ – степень
разброса значений этой величины по
отношению к ее центру.
35. Дисперсия св и ее свойства. Среднее квадратическое отклонение.
Дисперсия
– оценка разброса, МО квадрата отклонения
СВ от ее МО, т.е.
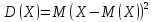 .
Если ДСВ Х, то
.
Если ДСВ Х, то
 .
Дисперсия обладает тем недостатком,
что ее размерность не совпадает с
размерностью СВ, поэтому вводится еще
и среднее квадратическое отклонение
.
Дисперсия обладает тем недостатком,
что ее размерность не совпадает с
размерностью СВ, поэтому вводится еще
и среднее квадратическое отклонение
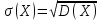 .
Свойства дисперсии – 1) Дисперсия
постоянно величины всегда =0, т.е. D(C)=0,
C=const.
Действительно,
.
Свойства дисперсии – 1) Дисперсия
постоянно величины всегда =0, т.е. D(C)=0,
C=const.
Действительно,
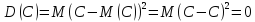 ;
2) Постоянный множитель можно выносить
за знак дисперсии, но сначала возведя
в квадрат, т.е.
;
2) Постоянный множитель можно выносить
за знак дисперсии, но сначала возведя
в квадрат, т.е.
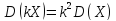 ;
3) Дисперсия алгебраической суммы 2-х
независимых СВ = сумме их дисперсий,
т.е.
;
3) Дисперсия алгебраической суммы 2-х
независимых СВ = сумме их дисперсий,
т.е.
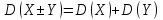 ;
4) Дисперсия СВ = разности между МО
квадрата СВ и квадратом ее МО т.е.
;
4) Дисперсия СВ = разности между МО
квадрата СВ и квадратом ее МО т.е.
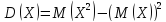 .
.
36. Биномиальное распределение и его числовые характеристики.
Биномиальным
называют распределение вероятностей,
определяемое формулой Бернулли. Закон
назван биномиальным потому, что правая
часть равенства – общий член разложения
бинома Ньютона –
 …
Первый член разложения pn
определяет вероятность наступления
события n раз в n
независимых опытах, 2-ой член npn-1q
определяет вероятность наступления
события (n-1) раз, … , qn
– последний член определяет вероятность
того, что событие не появится ни разу.
…
Первый член разложения pn
определяет вероятность наступления
события n раз в n
независимых опытах, 2-ой член npn-1q
определяет вероятность наступления
события (n-1) раз, … , qn
– последний член определяет вероятность
того, что событие не появится ни разу.
Теорема – МО биномиального распределения с параметрами n и р = произведению np, т.е. M(X)=np. Теорема – Дисперсия биномиального распределения с параметрами n и p = произведению npq, т.е. D(X)=npq.
