7. Определение криволинейных интегралов 2-го рода, свойства, вычисление, применение.
(интегральная сумма). Если при
существует предел интегральных сумм,
не зависящий ни от способа разбиения
кривой
,
ни от выбора точек Ni
в каждой из них – криволинейный интеграл
2-го рода от вектор-функции
по кривой
(P,R,Q
– функции непрерывные в точках гладкой
кривой). Вычисление – 1)
.
2)
.
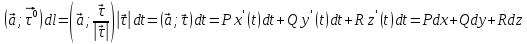3)
.
Формула для вычисления криволинейного
интеграла 2-го рода в случае параметрического
задания кривой –
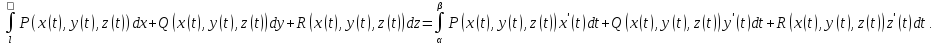Если кривая плоская и
(P,Q),
то
.
Свойства – 1) Линейность –
;
2) Аддитивность –
;
3) Интеграл зависит от ее ориентации,
т.е.
.
8. Формула Грина.
Связывает
криволинейный интеграл 2-го рода по
замкнутой кривой с 2-ым интегралом по
области, ограниченной этой кривой. Пусть
P(x;y)
и Q(x;y)
– функции, непрерывные вместе со своими
частными производными
в области σ, тогда
.
Контур L проходится в +
направлении, т.е. при движении вдоль
него, область σ находится слева.
9. Числовые ряды. Сходимость ряда и его сумма.
Числовым
рядом называется выражение
.
an
– общий член ряда. Ряд считается заданным,
если известен общий член ряда, как
функция его номера n –
an=f(n).
Сумма Sn
1-ых n-членов ряда называется
n-ой частичной суммой ряда
–
.
Ряд сходящийся, если существует конечный
предел суммы S
последовательности его частичных сумм
Sn
при неограниченном возрастании
номера n –
.
Если последовательность частичных сумм
ряда не имеет предела, то ряд расходящийся
и суммы не имеет.
10. Необходимый признак сходимости. Гармонический ряд.
Теорема –
Если ряд
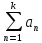сходится, то его общий член стремится
к 0, т.е.
.
Пусть сходящийся ряд имеет сумму S,
рассмотрим его частичные суммы –
,
значит
.
Т.к.
.
Следствие (достаточный признак
расходимости ряда) – Если предел ≠0 или
не существует, то ряд
расходится. Однако, существуют расходящиеся
ряды, для которых предел =0. Гармонический
ряд –
- ряд всегда расходится.
11. Достаточные признаки сходимости рядов с положительными членами: Даламбера, Коши, интегральный признак Коши, признаки сравнения.
Теорема
(признак сравнения) – Пусть для членов
рядов
имеет место неравенство
–
1) Если ряд
сходится, то сходится и ряд
;
2) Если ряд
расходится, то расходится и ряд
.
Теорема (предельные признаки сравнения)
– Пусть члены рядов
положительны и существует
,
тогда ряды одновременно сходятся и
расходятся (L>0 –
расходятся). Теорема (признак Даламбера)
– Если для знакоположительного ряда
существует предел отношения последующего
члена ряда к предыдущему, при неограниченном
возрастании номера n, т.е.
,
то при q<1 ряд сходится,
при q>1 – расходится.
Теорема (признак Коши) – Если все члены
ряда
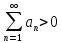и существует предел
,
то при k<1 ряд сходится,
а при k>1 – расходится.
Теорема (интегральный признак Коши) –
Пусть члены знакоположительного ряда
являются значениями при
некоторой функции f(x),
положительной, непрерывной, убывающей
на интервале
так, что
,
тогда – 1) Если сходится
,
то сходится и ряд; 2) Если расходится
интеграл, то расходится и ряд.