
- •2. Двойные интегралы в полярной системе координат.
- •3. Тройные интегралы, их свойства и вычисление в декартовых координатах.
- •4. Тройной интеграл в цилиндрической и сферической системах координат.
- •5. Приложения двойных и тройных интегралов.
- •6. Определение криволинейного интеграла 1-го рода, свойства, вычисление, применение.
- •7. Определение криволинейных интегралов 2-го рода, свойства, вычисление, применение.
- •8. Формула Грина.
- •9. Числовые ряды. Сходимость ряда и его сумма.
- •10. Необходимый признак сходимости. Гармонический ряд.
- •11. Достаточные признаки сходимости рядов с положительными членами: Даламбера, Коши, интегральный признак Коши, признаки сравнения.
- •12. Ряд Дирихле и его сходимость.
- •13. Знакочередующиеся ряды. Признак Лейбница.
- •14. Знакопеременные ряды. Абсолютная и условная сходимость.
- •15. Функциональные ряды. Основные понятия. Область сходимости.
- •16. Степенные ряды. Радиус и интервал сходимости. Теорема Абеля.
- •17. Разложение функций в степенные ряды. Ряды Тейлора и Маклорена.
- •18. Применение степенных рядов к приближенным вычислениям.
- •19. Элементы комбинаторики.
- •20. Основные понятия теории вероятностей.
- •21. Пространство элементарных событий. Алгебра событий.
- •22. Классическое и статистическое определение вероятности и ее свойства.
- •23. Теоремы сложения вероятностей.
- •24. Условная вероятность. Теоремы умножения вероятностей.
- •25. Формула полной вероятности. Формула Байеса.
- •26. Схема испытаний Бернулли. Формула Бернулли.
- •27. Предельные теоремы в схеме Бернулли: Пуассона, Муавра-Лапласа.
- •28. Наивероятнейшее число появлений события при повторных испытаниях по схеме Бернулли.
- •29. Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях.
- •30. Дискретные случайные величины и законы их распределения.
- •31. Непрерывные случайные величины и законы их распределения.
- •32. Функция распределения вероятностей св и ее свойства.
- •33. Дифференциальная функция распределения непрерывной св (плотность распределения св) и ее свойства.
- •34. Математическое ожидание св и ее свойства.
- •35. Дисперсия св и ее свойства. Среднее квадратическое отклонение.
- •36. Биномиальное распределение и его числовые характеристики.
- •37. Равномерное и показательное распределения, их числовые характеристики.
- •38. Нормальное распределение и его числовые характеристики.
26. Схема испытаний Бернулли. Формула Бернулли.
Последовательные
опыты независимые, если вероятность
осуществления любого исхода в каждом
n-ом опыте не зависит от
реализации исходов предыдущих испытаний.
Серию независимых испытаний с одной и
той же вероятностью успеха р=Р(А) называют
испытаниями или схемой Бернулли. Формула
Бернулли –
 .
Вероятность того, что при n
испытаниях событие А наступит m
раз, значит не появится (n-m)
раз.
.
Вероятность того, что при n
испытаниях событие А наступит m
раз, значит не появится (n-m)
раз.
27. Предельные теоремы в схеме Бернулли: Пуассона, Муавра-Лапласа.
Формула
Бернулли при больших n
приводит к сложным вычислениям. Теорема
(Пуассона, при большом n
и очень маленьком р) – Пусть вероятность
события А при каждом испытании в серии
из n независимых опытов
=
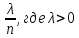 – постоянная независящая от n,
значит вероятность Pn(m)
при
– постоянная независящая от n,
значит вероятность Pn(m)
при
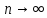 и фиксированном m стремится
к
и фиксированном m стремится
к
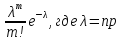 .
Теорема (локальная теорема Муавра-Лапласа
при больших n) – Пусть
вероятность события А в n
независимых опытах = p
(0<p<1), то Pn(m)
того, что в этих опытах событие А наступит
m раз удовлетворяет при
.
Теорема (локальная теорема Муавра-Лапласа
при больших n) – Пусть
вероятность события А в n
независимых опытах = p
(0<p<1), то Pn(m)
того, что в этих опытах событие А наступит
m раз удовлетворяет при
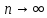 соотношению
соотношению
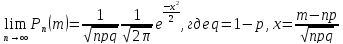 .
Или же при достаточно больших n
и если р не слишком близка к 0 или 1, имеем
.
Или же при достаточно больших n
и если р не слишком близка к 0 или 1, имеем
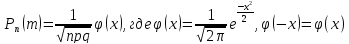 .
Теорема (интегральная теорема
Муавра-Лапласа при больших n)
– Пусть m – числа наступлений
события А в серии из n
независимых испытаний, р – вероятность
наступления события А при каждом опыте
(0<p<1), значит
.
Теорема (интегральная теорема
Муавра-Лапласа при больших n)
– Пусть m – числа наступлений
события А в серии из n
независимых испытаний, р – вероятность
наступления события А при каждом опыте
(0<p<1), значит
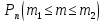 того, что в этих опытах событие А появится
не менее m1 и не более
m2 раз удовлетворяет
при
того, что в этих опытах событие А появится
не менее m1 и не более
m2 раз удовлетворяет
при
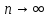 соотношению
соотношению
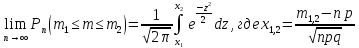 .
Или же
.
Или же
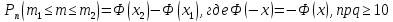 .
.
28. Наивероятнейшее число появлений события при повторных испытаниях по схеме Бернулли.
При некотором
числе m0 вероятность
Pn(m),
как функция целочисленного аргумента
m, достигает своего
наибольшего значения. m0
– наивероятнейшее число появления
события А в серии из n
испытаний и удовлетворяет неравенству
 .
.
29. Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях.
Пусть n
– число опытов, р – вероятность появления
события А в каждом опыте,
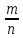 – относительная частота появления
события А. Найдем вероятность
– относительная частота появления
события А. Найдем вероятность
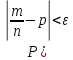 )
того, что отклонение относительной
частоты от постоянной вероятности не
превосходит ε.
)
того, что отклонение относительной
частоты от постоянной вероятности не
превосходит ε.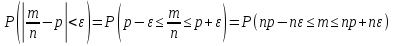 .
Из интегральной формулы следует, что
.
Из интегральной формулы следует, что
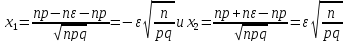 .
X2 – искомая
вероятность.
.
X2 – искомая
вероятность.
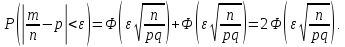
30. Дискретные случайные величины и законы их распределения.
СВ – величина, которая в результате опыта со случайным исходом принимает то или иное значение. Закон распределения – любое правило, устанавливающее связь между возможными значениями СВ и их вероятностями. CВ называется дискретной, если возможные значения могут быть перечислены, т.е. пронумерованы одно за другим, или же если множество значений конечно или счетно. Простейшая форму закона распределения ДСВ – ряд распределения, таблица, в верхней строке которой перечислены все значения СВ в порядке возрастания, а в нижней – соответствующие вероятности. Сумма всех вероятностей =1. Функция распределения ДСВ по Х есть неразрывная ступенчатая функция, скачки которой соответствуют возможным значениям хn СВ Х и равны вероятностям этих значений.
Закон
распределения Пуассона вероятностей
массовых (n велико) и редких (p<0,1)
событий –
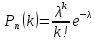 .
МО закона распределения Пуассона
Pk=P(X=k)
–
.
МО закона распределения Пуассона
Pk=P(X=k)
–
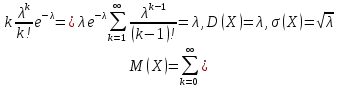 .
.
