18. Применение степенных рядов к приближенным вычислениям.

19. Элементы комбинаторики.

Комбинаторика – раздел математики, изучает сколько комбинаций определенного типа можно составить из данных элементов. Перестановки – комбинации, состоящие из одних и тех же n-различных элементов и отличающихся только порядком их расположения (P_n=n!). Размещения – комбинации, составленные из n-различных элементов по m элементов, отличающиеся либо составом элементов, либо их порядком (). Сочетания – комбинации, составленные из n-различных элементов по m элементов, которые отличаются хотя бы 1 элементом ().

20. Основные понятия теории вероятностей.

Теория вероятностей – математическая наука, изучает закономерности в случайных явлениях. Опыт (эксперимент, испытание) – осуществление конкретного комплекса условий (подбрасывание монеты, стрельба по мишени). Событие – всякий результат опыта или наблюдения. Случайное событие – если в результате опыта оно может произойти, а может и не произойти (обозначаются А,В,С…). Достоверное событие – если оно обязательно произойдет в условиях данного опыта. Невозможное событие – если оно в условиях данного опыта не может произойти. Элементарные события – которые нельзя разложить на более простые, а все остальные события – составные. Множество всех элементарных событий – пространство элементарных событий , а сами элементарные события (исходы опыта) – точки ω этого пространства. Несовместные события – если появление одного из них исключает появление других событий в условиях одного и того же опыта. 2 события – совместны – если появление одного из них не исключает появление другого в одном и том же испытании. Противоположное событие – состоит в ненаступлении события (обозначается ). Несколько событий в условиях одного опыта образуют полную группу – если в результате произойдет хотя бы одно из них, т.е. .

21. Пространство элементарных событий. Алгебра событий.

Между событиями могут существовать соотношения – 1) Если из того, что произошло событие А следует, что произошло и В, то А влечет за собой В и обозначается ; 2) Если одновременно А влечет В и В влечет А, то события А и В – равносильные, при этом А=В.

Событие, состоящее в том, что произойдет хотя бы 1 из 2-х события А и В (не важно какие или оба) – сумма этих событий и обозначается А+В или .

Событие, состоящее в одновременном наступлении событий А и В – произведение этих событий и обозначается АВ или .

Операции сложения и произведения – 1) А+В=В+А; 2) A+(B+C)=(A+C)+B; 3) AB=BA; 4) A(BC)=(AB)C; 5) A(B+C)=AB+AC.

22. Классическое и статистическое определение вероятности и ее свойства.

Цель теории вероятностей – вычисление вероятностей событий, их комбинаций и изучение свойств вероятностей. Классической вероятностью Р(А) события А называется отношение числа m элементарных исходов, благоприятствующих событию А к числу n всех элементарных исходов, т.е. 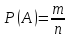. Свойства – 1) Вероятность достоверного события ; 2) Вероятность невозможного события ; 3) Вероятность любого события А удовлетворяет неравенству . Статистической вероятностью называется число, характеризующее частоту события при большом числе испытаний, т.е. числа, около которого частота события колеблется .