
- •2. Двойные интегралы в полярной системе координат.
- •3. Тройные интегралы, их свойства и вычисление в декартовых координатах.
- •4. Тройной интеграл в цилиндрической и сферической системах координат.
- •5. Приложения двойных и тройных интегралов.
- •6. Определение криволинейного интеграла 1-го рода, свойства, вычисление, применение.
- •7. Определение криволинейных интегралов 2-го рода, свойства, вычисление, применение.
- •8. Формула Грина.
- •9. Числовые ряды. Сходимость ряда и его сумма.
- •10. Необходимый признак сходимости. Гармонический ряд.
- •11. Достаточные признаки сходимости рядов с положительными членами: Даламбера, Коши, интегральный признак Коши, признаки сравнения.
- •12. Ряд Дирихле и его сходимость.
- •13. Знакочередующиеся ряды. Признак Лейбница.
- •14. Знакопеременные ряды. Абсолютная и условная сходимость.
- •15. Функциональные ряды. Основные понятия. Область сходимости.
- •16. Степенные ряды. Радиус и интервал сходимости. Теорема Абеля.
- •17. Разложение функций в степенные ряды. Ряды Тейлора и Маклорена.
- •18. Применение степенных рядов к приближенным вычислениям.
- •19. Элементы комбинаторики.
- •20. Основные понятия теории вероятностей.
- •21. Пространство элементарных событий. Алгебра событий.
- •22. Классическое и статистическое определение вероятности и ее свойства.
- •23. Теоремы сложения вероятностей.
- •24. Условная вероятность. Теоремы умножения вероятностей.
- •25. Формула полной вероятности. Формула Байеса.
- •26. Схема испытаний Бернулли. Формула Бернулли.
- •27. Предельные теоремы в схеме Бернулли: Пуассона, Муавра-Лапласа.
- •28. Наивероятнейшее число появлений события при повторных испытаниях по схеме Бернулли.
- •29. Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях.
- •30. Дискретные случайные величины и законы их распределения.
- •31. Непрерывные случайные величины и законы их распределения.
- •32. Функция распределения вероятностей св и ее свойства.
- •33. Дифференциальная функция распределения непрерывной св (плотность распределения св) и ее свойства.
- •34. Математическое ожидание св и ее свойства.
- •35. Дисперсия св и ее свойства. Среднее квадратическое отклонение.
- •36. Биномиальное распределение и его числовые характеристики.
- •37. Равномерное и показательное распределения, их числовые характеристики.
- •38. Нормальное распределение и его числовые характеристики.
12. Ряд Дирихле и его сходимость.
Ряд Дирихле
(обобщенный гармонический) –
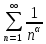 .
Если
.
Если
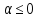 ,
то
,
то
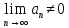 – ряд расходится по необходимому
признаку сходимости. Если
– ряд расходится по необходимому
признаку сходимости. Если
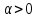 ,
то по интегральному признаку Коши
получаем, что при
,
то по интегральному признаку Коши
получаем, что при
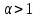 ряд Дирихле сходится, и расходится, при
ряд Дирихле сходится, и расходится, при
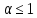 .
.
13. Знакочередующиеся ряды. Признак Лейбница.
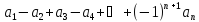 .
Теорема (признак Лейбница) – Если
абсолютные величины членов знакочередующегося
ряда монотонно убывают, т.е.
.
Теорема (признак Лейбница) – Если
абсолютные величины членов знакочередующегося
ряда монотонно убывают, т.е.
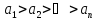 ,
и общий член ряда стремится к 0, т.е.
,
и общий член ряда стремится к 0, т.е.
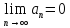 ,
то ряд сходится (
,
то ряд сходится (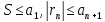 .
.
14. Знакопеременные ряды. Абсолютная и условная сходимость.
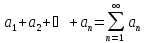 (числа могут быть как >, так и <0,
расположение знаков произвольно).
(числа могут быть как >, так и <0,
расположение знаков произвольно).
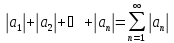 – ряд из абсолютных величин. Теорема
(достаточный признак сходимости) – Если
сходится ряд из абсолютных величин, то
сходится и знакопеременный ряд. Но,
например, ряд
– ряд из абсолютных величин. Теорема
(достаточный признак сходимости) – Если
сходится ряд из абсолютных величин, то
сходится и знакопеременный ряд. Но,
например, ряд
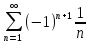 по признаку Лейбница сходится, а ряд из
абсолютных величин его членов, т.е.
гармонический, расходится. Все сходящиеся
ряды делятся на абсолютно и условно
сходящиеся. Абсолютно – сходящиеся
ряды, для которых ряды, составленные из
модулей их членов также сходятся. Условно
– сходящиеся ряды, для которых ряды,
составленные из модулей их членов
расходятся.
по признаку Лейбница сходится, а ряд из
абсолютных величин его членов, т.е.
гармонический, расходится. Все сходящиеся
ряды делятся на абсолютно и условно
сходящиеся. Абсолютно – сходящиеся
ряды, для которых ряды, составленные из
модулей их членов также сходятся. Условно
– сходящиеся ряды, для которых ряды,
составленные из модулей их членов
расходятся.
15. Функциональные ряды. Основные понятия. Область сходимости.
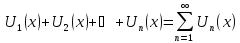 (Un(x)
– функции, определенные в некоторой
области изменения аргумента х). Если
вместо х положить х0 из области
Un(x),
то получим числовой ряд (может и сходится,
и расходится). Если он сходится, то x0
– точка сходимости функционального
ряда, если же расходится, то x0 –
точка расходимости. Область сходимости
– совокупность всех точек сходимости.
Частичная сумма Sn(x)
– функция переменной х, определенная
в области сходимости. Если ряд сходится
и имеет сумму S(x),
то разность S(x)–Sn(x)
– n-ый остаток (rn(x)),
причем
(Un(x)
– функции, определенные в некоторой
области изменения аргумента х). Если
вместо х положить х0 из области
Un(x),
то получим числовой ряд (может и сходится,
и расходится). Если он сходится, то x0
– точка сходимости функционального
ряда, если же расходится, то x0 –
точка расходимости. Область сходимости
– совокупность всех точек сходимости.
Частичная сумма Sn(x)
– функция переменной х, определенная
в области сходимости. Если ряд сходится
и имеет сумму S(x),
то разность S(x)–Sn(x)
– n-ый остаток (rn(x)),
причем
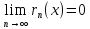 .
.
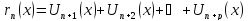 .
.
РАВНОМЕРНО СХОДЯЩИЕСЯ ФР И ИХ СВОЙСТВА?!?!?!
16. Степенные ряды. Радиус и интервал сходимости. Теорема Абеля.
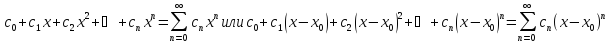 (cn –
коэффициент степенного ряда). Степенной
ряд всегда сходится, по крайней мере в
х=0 и х=х0 соответственно. Теорема
Абеля – Пусть степенной ряд сходится
в точке
(cn –
коэффициент степенного ряда). Степенной
ряд всегда сходится, по крайней мере в
х=0 и х=х0 соответственно. Теорема
Абеля – Пусть степенной ряд сходится
в точке
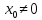 ,
тогда он сходится абсолютно в любой
точке х, удовлетворяющей неравенству
,
тогда он сходится абсолютно в любой
точке х, удовлетворяющей неравенству
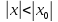 и сходится равномерно в области
и сходится равномерно в области
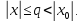 Если же ряд расходится в некоторой точке
x1, то он расходится
и во всех точках х таких, что
Если же ряд расходится в некоторой точке
x1, то он расходится
и во всех точках х таких, что
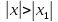 .
Теорема Абеля геометрически утверждает,
что если x0 – точка
сходимости, то во всех точках на интервале
.
Теорема Абеля геометрически утверждает,
что если x0 – точка
сходимости, то во всех точках на интервале
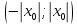 ряд сходится абсолютно, а если x1
– точка расходимости, то во всех точках
вне интервала
ряд сходится абсолютно, а если x1
– точка расходимости, то во всех точках
вне интервала
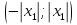 ряд расходится.
ряд расходится.
Если
степенной ряд сходится не при всех
значениях х, то существует число R>0
такое, что ряд абсолютно сходится при
|x|<R и
расходится при |x|>R.
Интервал (-R; R)
– интервал сходимости степенного ряда,
где R – радиус. Любой
степенной ряд имеет свой радиус сходимости
и при
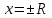 ряд может либо сходится, либо расходится.
Для отыскания радиуса, используют
признак Коши (
ряд может либо сходится, либо расходится.
Для отыскания радиуса, используют
признак Коши (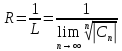 – формула Коши-Адамара) или Даламбера
(
– формула Коши-Адамара) или Даламбера
(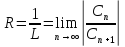 ),
при этом, если L=0, то ряд
сходится на всей числовой прямой.
),
при этом, если L=0, то ряд
сходится на всей числовой прямой.
СВОЙСТВА?!?!?
17. Разложение функций в степенные ряды. Ряды Тейлора и Маклорена.
Пусть f(x)
в некоторой окрестности точки x0
имеет производные всех порядков. Ряд
Тэйлора функции f(x)
в точке x0 –
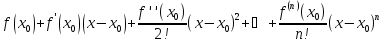 .
Если же х0=0, то имеем ряд Маклорена
–
.
Если же х0=0, то имеем ряд Маклорена
–
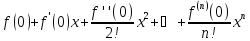 .
Ряд Тейлора, составленный для f(x),
может расходится или сходится, но не к
f(x). Если же
ряд сходится к f(x),
то справедливо
.
Ряд Тейлора, составленный для f(x),
может расходится или сходится, но не к
f(x). Если же
ряд сходится к f(x),
то справедливо
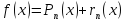 ,
где rn
– остаток ряда. Для сходимости ряда
Тейлора к f(x)
необходимо и достаточно выполнение
условия
,
где rn
– остаток ряда. Для сходимости ряда
Тейлора к f(x)
необходимо и достаточно выполнение
условия
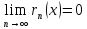 .
Остаточный член в форме Лагранжа
.
Остаточный член в форме Лагранжа
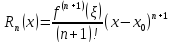 .
Теорема – Если производные любого
порядка k=0,1,2,… функции
ограничены в окрестности точки x0
одной и той же k=const,
то ряд Тейлора сходится к f(x)
для любого х из этой окрестности. Теорема
– Если f(x)
разложится в ряд Тейлора, то это разложение
единственно. f(x)=ex,
тогда
.
Теорема – Если производные любого
порядка k=0,1,2,… функции
ограничены в окрестности точки x0
одной и той же k=const,
то ряд Тейлора сходится к f(x)
для любого х из этой окрестности. Теорема
– Если f(x)
разложится в ряд Тейлора, то это разложение
единственно. f(x)=ex,
тогда
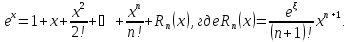 Т.к.
Т.к.
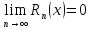 для любого х, то ряд сходится при любых
х. Если же заменить х на –х, получим
для любого х, то ряд сходится при любых
х. Если же заменить х на –х, получим
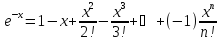 ,
также сходится на всей числовой прямой.
,
также сходится на всей числовой прямой.
