
- •2. Двойные интегралы в полярной системе координат.
- •3. Тройные интегралы, их свойства и вычисление в декартовых координатах.
- •4. Тройной интеграл в цилиндрической и сферической системах координат.
- •5. Приложения двойных и тройных интегралов.
- •6. Определение криволинейного интеграла 1-го рода, свойства, вычисление, применение.
- •7. Определение криволинейных интегралов 2-го рода, свойства, вычисление, применение.
- •8. Формула Грина.
- •9. Числовые ряды. Сходимость ряда и его сумма.
- •10. Необходимый признак сходимости. Гармонический ряд.
- •11. Достаточные признаки сходимости рядов с положительными членами: Даламбера, Коши, интегральный признак Коши, признаки сравнения.
- •12. Ряд Дирихле и его сходимость.
- •13. Знакочередующиеся ряды. Признак Лейбница.
- •14. Знакопеременные ряды. Абсолютная и условная сходимость.
- •15. Функциональные ряды. Основные понятия. Область сходимости.
- •16. Степенные ряды. Радиус и интервал сходимости. Теорема Абеля.
- •17. Разложение функций в степенные ряды. Ряды Тейлора и Маклорена.
- •18. Применение степенных рядов к приближенным вычислениям.
- •19. Элементы комбинаторики.
- •20. Основные понятия теории вероятностей.
- •21. Пространство элементарных событий. Алгебра событий.
- •22. Классическое и статистическое определение вероятности и ее свойства.
- •23. Теоремы сложения вероятностей.
- •24. Условная вероятность. Теоремы умножения вероятностей.
- •25. Формула полной вероятности. Формула Байеса.
- •26. Схема испытаний Бернулли. Формула Бернулли.
- •27. Предельные теоремы в схеме Бернулли: Пуассона, Муавра-Лапласа.
- •28. Наивероятнейшее число появлений события при повторных испытаниях по схеме Бернулли.
- •29. Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях.
- •30. Дискретные случайные величины и законы их распределения.
- •31. Непрерывные случайные величины и законы их распределения.
- •32. Функция распределения вероятностей св и ее свойства.
- •33. Дифференциальная функция распределения непрерывной св (плотность распределения св) и ее свойства.
- •34. Математическое ожидание св и ее свойства.
- •35. Дисперсия св и ее свойства. Среднее квадратическое отклонение.
- •36. Биномиальное распределение и его числовые характеристики.
- •37. Равномерное и показательное распределения, их числовые характеристики.
- •38. Нормальное распределение и его числовые характеристики.
с1. Двойные интегралы, их свойства и вычисление в декартовых координатах.
Двойным
интегралом от функции z=f(x,y)
по области
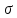 называется предел, к которому стремится
интегральная сумма при неограниченном
увеличении числа n-малых
площадок
называется предел, к которому стремится
интегральная сумма при неограниченном
увеличении числа n-малых
площадок
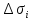 при условии, что каждая из них стягивается
в точку.
при условии, что каждая из них стягивается
в точку.
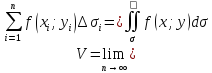 .
Теорема (о существовании) – Для всякой
функции z=f(x,y),
непрерывной в ограниченной замкнутой
области, имеющей площадь
.
Теорема (о существовании) – Для всякой
функции z=f(x,y),
непрерывной в ограниченной замкнутой
области, имеющей площадь
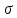 ,
существует 2-ой интеграл. Свойства – 1)
Постоянный множитель можно выносить
за знак интеграла; 2) 2-ой интеграл
алгебраической суммы = алгебраической
сумме 2-ых интегралов; 3) Если в области
интегрирования
,
существует 2-ой интеграл. Свойства – 1)
Постоянный множитель можно выносить
за знак интеграла; 2) 2-ой интеграл
алгебраической суммы = алгебраической
сумме 2-ых интегралов; 3) Если в области
интегрирования
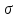 имеет место неравенство
имеет место неравенство
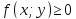 ,
то и
,
то и
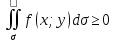 ;
4) Если в области интегрирования
;
4) Если в области интегрирования
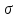 имеет место неравенство
имеет место неравенство
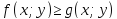 ,
то и
,
то и
 ;
5) Если область интегрирования
;
5) Если область интегрирования
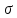 разбита на несколько частей
разбита на несколько частей
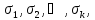 то
то
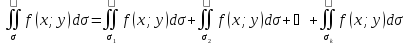 ;
6) Теорема (о среднем) – Пусть функция
f(x,y)
непрерывна в замкнутой ограниченной
области σ, тогда в области σ существует
такая точка P0(x0;y0),
что
;
6) Теорема (о среднем) – Пусть функция
f(x,y)
непрерывна в замкнутой ограниченной
области σ, тогда в области σ существует
такая точка P0(x0;y0),
что
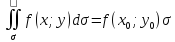 .
Теорема – Пусть функция f(x,y)
непрерывна в замкнутой прямоугольной
D, тогда имеет место
равенство
.
Теорема – Пусть функция f(x,y)
непрерывна в замкнутой прямоугольной
D, тогда имеет место
равенство
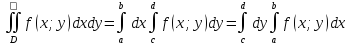 .
Пусть любая прямая || оси Оу пересекает
границу области D не более,
чем в 2-ух точках, тогда справедлива
формула
.
Пусть любая прямая || оси Оу пересекает
границу области D не более,
чем в 2-ух точках, тогда справедлива
формула
 .
Если область D определена
неравенством
.
Если область D определена
неравенством
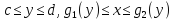 и любая прямая || оси Ох пересекает
границу области не более, чем в 2-ух
точках, то
и любая прямая || оси Ох пересекает
границу области не более, чем в 2-ух
точках, то
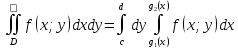 .
.
2. Двойные интегралы в полярной системе координат.
 .
Теорема – Если преобразования x
и y переводит область σ в
область σ* и если функции х и у
имеют в области σ* непрерывные
частные производные 1-го порядка и ≠0
Якобиан I, то при условии
существования 2-го интеграла справедлива
формула замены переменных.
.
Теорема – Если преобразования x
и y переводит область σ в
область σ* и если функции х и у
имеют в области σ* непрерывные
частные производные 1-го порядка и ≠0
Якобиан I, то при условии
существования 2-го интеграла справедлива
формула замены переменных. .
.
3. Тройные интегралы, их свойства и вычисление в декартовых координатах.
Если
существует
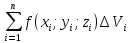 (интегральная
сумма) и не зависит ни от способа разбиения
V на малые тела
(интегральная
сумма) и не зависит ни от способа разбиения
V на малые тела
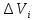 ,
ни от выбора в каждом из них точки
Pi(xi;yi;zi),
то его называют 3-ым интегралом от функции
u=f(x;y;z)
по области
,
ни от выбора в каждом из них точки
Pi(xi;yi;zi),
то его называют 3-ым интегралом от функции
u=f(x;y;z)
по области
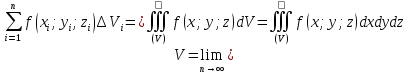 .
Теорема (о существовании) – Для всякой
функции u=f(x;y;z),
непрерывной в ограниченной замкнутой
области пространства, имеющей объем V,
существует 3-ой интеграл. Свойства – 1)
Постоянный множитель можно выносить
за знак интеграла; 2) 3-ой интеграл
алгебраической суммы = алгебраической
сумме 3-ых интегралов; 3) Если в области
интегрирования
.
Теорема (о существовании) – Для всякой
функции u=f(x;y;z),
непрерывной в ограниченной замкнутой
области пространства, имеющей объем V,
существует 3-ой интеграл. Свойства – 1)
Постоянный множитель можно выносить
за знак интеграла; 2) 3-ой интеграл
алгебраической суммы = алгебраической
сумме 3-ых интегралов; 3) Если в области
интегрирования
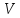 имеет место неравенство
имеет место неравенство
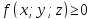 ,
то и
,
то и
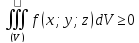 ;
4) Если в области интегрирования
;
4) Если в области интегрирования
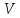 имеет место неравенство
имеет место неравенство
 ,
то и
,
то и
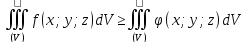 ;
5) Если область интегрирования
;
5) Если область интегрирования
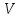 разбита на несколько частей
разбита на несколько частей
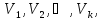 то
то
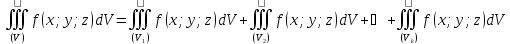 ;
6) Теорема (о среднем) – Если функция
f(x;y;z)
непрерывна в замкнутой ограниченной
области V, то в этой области
существует такая точка P0(x0;y0;z0),
что
;
6) Теорема (о среднем) – Если функция
f(x;y;z)
непрерывна в замкнутой ограниченной
области V, то в этой области
существует такая точка P0(x0;y0;z0),
что
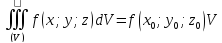 ;
7) Если в области V –
f(x;y;z)=1,
то 3-ой интеграл численно = объему (V)
области, т.е.
;
7) Если в области V –
f(x;y;z)=1,
то 3-ой интеграл численно = объему (V)
области, т.е.
 .
Пусть V – параллелепипед
.
Пусть V – параллелепипед
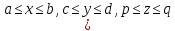 ),
тогда
),
тогда
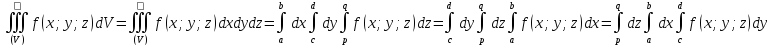 .
Пусть область V задана
неравенствами
.
Пусть область V задана
неравенствами
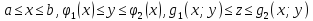 ,
тогда
,
тогда
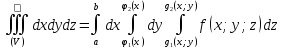 .
.
4. Тройной интеграл в цилиндрической и сферической системах координат.
 .
.
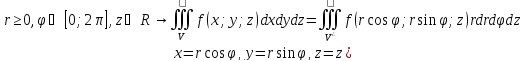 .
– Цилиндрические координаты (r,
ϕ, z). Cферические
координаты
.
– Цилиндрические координаты (r,
ϕ, z). Cферические
координаты
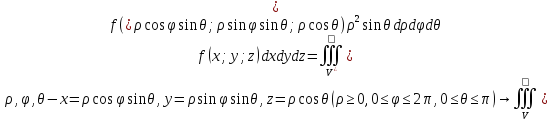 .
.
5. Приложения двойных и тройных интегралов.
2-ой интеграл
- 1) Вычисление объемов – объем V
криволинейного цилиндра, ограниченного
сверху поверхностью
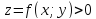 ,
снизу плоскостью z=0 и с
боков прямой цилиндрической поверхностью,
вырезающей на плоскости Oxy
область σ -
,
снизу плоскостью z=0 и с
боков прямой цилиндрической поверхностью,
вырезающей на плоскости Oxy
область σ -
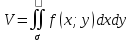 .
2) Вычисление площадей – Если положить
f(x;y)≡1
всюду в области σ, то получаем выражение
площади S области σ в виде
2-го интеграла
.
2) Вычисление площадей – Если положить
f(x;y)≡1
всюду в области σ, то получаем выражение
площади S области σ в виде
2-го интеграла
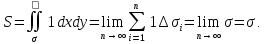 3) Вычисление массы пластинки – Масса
плоской пластинки σ с плотностью
3) Вычисление массы пластинки – Масса
плоской пластинки σ с плотностью
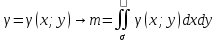 – физический смысл 2-го интеграла. 4)
Вычисление координат центра масс
пластинки –
– физический смысл 2-го интеграла. 4)
Вычисление координат центра масс
пластинки –
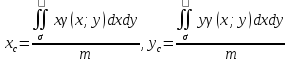 ,
числители My
и Mx
соответственно – статистические моменты
относительно Oy и Ох. 3-ой
интеграл – 1) Вычисление объемов -
,
числители My
и Mx
соответственно – статистические моменты
относительно Oy и Ох. 3-ой
интеграл – 1) Вычисление объемов -
 .
2) Вычисление массы тела -
.
2) Вычисление массы тела -
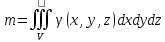 .
3) Вычисление координат центра масс
пространственного тела –
.
3) Вычисление координат центра масс
пространственного тела –
 ,
числители – статистические моменты
материальной точки массы, относительно
плоскостей OYZ, OXZ,
OXY. Если рассматриваемое
тело однородно, т.е.
,
числители – статистические моменты
материальной точки массы, относительно
плоскостей OYZ, OXZ,
OXY. Если рассматриваемое
тело однородно, т.е.
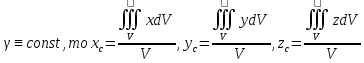 .
.
6. Определение криволинейного интеграла 1-го рода, свойства, вычисление, применение.
Кривая,
заданная уравнениями x=x(t),
y=y(t)
– гладкая, если функции непрерывны и
имеют непрерывные производные, не
обращающиеся в 0 одновременно, т.е. кривая
в каждой точке имеет касательную.
Непрерывная кривая, составленная из
конечного числа гладких кусков –
кусочно-гладкая.
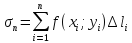 (интегральная сумма). Если существует
предел интегральной суммы, независящий
ни от способа разбиения дуги
(интегральная сумма). Если существует
предел интегральной суммы, независящий
ни от способа разбиения дуги
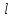 на части
на части
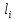 ,
ни от выбора точек (xi;yi)
в каждой из них, то этот предел называется
криволинейным интегралом 1-го рода по
дуге
,
ни от выбора точек (xi;yi)
в каждой из них, то этот предел называется
криволинейным интегралом 1-го рода по
дуге
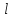 от функции f(x;y)
–
от функции f(x;y)
–
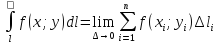 (то же самое и с 3-мя координатами).
(то же самое и с 3-мя координатами).
 – длина i-той части
– длина i-той части
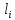 .
Вычисление – 1) В Декартовых координатах
–
.
Вычисление – 1) В Декартовых координатах
–
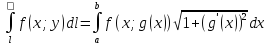 ;
2) Параметрически –
;
2) Параметрически –
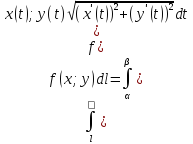 .
Свойства – 1) Линейность -
.
Свойства – 1) Линейность -
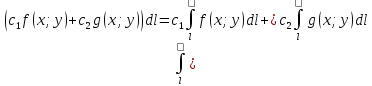 ;
2) Аддитивность – Если кусочно-гладкая
кривая
;
2) Аддитивность – Если кусочно-гладкая
кривая
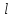 состоит из конечного числа гладких дуг
состоит из конечного числа гладких дуг
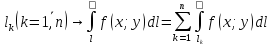 ;
3) Криволинейный интеграл не зависит от
направления пути интегрирование –
;
3) Криволинейный интеграл не зависит от
направления пути интегрирование –
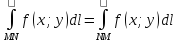 ;
4) Оценка модуля интеграла –
;
4) Оценка модуля интеграла –
 ;
5)
;
5)
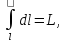 где L – длина дуги; 6)
Теорема (о среднем) – Если f(x;y)
непрерывна на кривой
где L – длина дуги; 6)
Теорема (о среднем) – Если f(x;y)
непрерывна на кривой
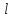 ,
то существует точка
,
то существует точка
 кривой
кривой
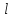 такая, что
такая, что
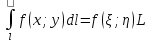 .
Применение – 1) Вычисление длины дуги
кривой
.
Применение – 1) Вычисление длины дуги
кривой
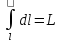 ;
2) Вычисление массы материальной дуги
–
;
2) Вычисление массы материальной дуги
–
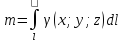 ;
3) Вычисление координат центра тяжести
материальной дуги –
;
3) Вычисление координат центра тяжести
материальной дуги –
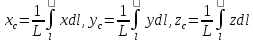 .
.
