Добавил:

citly Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский политехнический университет Петра Великого (бывш. СПбГПУ)

Предмет:

Высшая математика

Файл:

билеты 1 сем / все вместе.pdf

Скачиваний:

Добавлен:

18.01.2020

Размер:

6.68 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 55

Следовательно

а это противоречит тому, что □ Замечание 1. Теорема 2 по сути гласит, что во множестве значений

непрерывной на отрезке функции имеется наибольший и наименьший элементы. Они, соответственно, называются наибольшим и наименьшим

значениями функции, при этом точки и , в которых функция принимает эти значения, называются, соответственно точкой

максимума и точкой минимума функции на отрезке . Теорему 2, таким образом, можно рассматривать как теорему о существовании точек максимума и минимума непрерывной на отрезке функции.

Наибольшее и наименьшее значения функции на отрезке обычно обозначаются символами и

С учетом следствия из второй теоремы Больцано-Коши, из второй теоремы Вейерштрасса вытекает такое:

Следствие. Множество значений непрерывной на отрезке функции является отрезком , где , .

Контрпример - ?

35. Теорема Кантора.

Если функция определена и непрерывна на сегменте , то она равномерно непрерывна на .

Доказательство

Проведем доказательство методом от противного. Пусть не равномерно непрерывна на , тогда

, : .

Выберем последовательность , 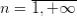. Согласно допущению, найдутся такие последовательности , , что:

, : : .

Последовательность ограничена и поэтому имеет подпоследовательность , которая сходится к элементу , причем

что . Тогда для подпоследовательности так же является пределом.

По условию теоремы — непрерывна на , поэтому

Это противоречит тому, что , .

Это противоречие и доказывает теорему.

Решим таким же методом, каким было проведено доказательство теоремы, пример.


Пример					скрыть
Пример

Доказать, что ограниченная и непрерывная функция				не является
равномерно непрерывной на		.
— ограничена и	непрерывна.		Тогда
:		.	Выберем		такие
подпоследовательности			.

можно выделить такие подпоследовательности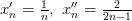

: . Следовательно, функция не является равномерно непрерывной на .

36. Теорема об односторонних пределах монотонной функции.


Если функция	определена и монотонна на отрезке		, то в каждой
точке	эта функция имеет конечные пределы слева и справа, а в
точках и правосторонний и левосторонний пределы.
Доказательство:
Пусть, например, функция		монотонно возрастает на	. Выберем

произвольную внутреннюю точку . Тогда

ограничена сверху на .

Согласно определению: а)

б) обозначим . Если , то .

Итог:

Итак	,	.
Аналогично доказываем, что функция имеет в точке			предел справа
причем	,	.
Следствие. Если функция определена и монотонна на интервале
,	предел справа и слева, причем если возрастает, то

если убывает, то

Мат. анализ. Вопросы 37-54

37. Теорема о достаточных условиях непрерывности функции на промежутке

Соответственно, для промежутка: все точки промежутка удовлетворяют данному равенству.

38. Теорема о монотонности и непрерывности обратной функции

TH. О обратной функции

Доказательство:

1) Монотонность:

2) Непрерывность:

39. Теорема о непрерывности основных элементарных и элементарных функций. Примеры

TH. О непрерывности элементарных функций

Все основные элементарные функции непрерывны при всех значениях X,

для которых они определены.

Доказательство:

Элементарная функция – формула, задаваемая конечным числом арифмитических действий и суперпозиций (операция взятия функции от функции) основных элементарных функций. Из основных теорем о непрерывности вытекает доказательство.

Примеры:

40. Определение производной функции в точке. Необходимое условие существования производной. Вычисление производных основных элементарных функций

( ) = ( )

Необходимое условие существования производной:

→

Вычисление производных основных элементарных функций:

41. Теоремы о производной суммы, произведения и частного.

42. Теорема о производной сложной функции. Примеры

Примеры:

43. Теорема о производной обратной функции. Примеры

Примеры:

44. Определение касательной к графику функции и теорема о достаточных условиях существования касательной к графику

45. Бесконечные и односторонние проивзодные. Примеры

Примеры:

46. Критерий дифференцируемости функций в точке. Следствие

Критерий дифференцируемости функции:

Для того чтобы функция F являлась дифференцируемой в данной точке X0,

необходимо и достаточно, чтобы она имела в этой точке конечную производную.

Следствие:

47. Определение, свойства и геометрический смысл дифференциала функции

Геометрический смысл:

Основные теоремы и свойства:

48. Свойства производной и дифференциала N-го порядка. Формула Лейбница

Свойства производной и дифференциала N-го порядка:

Формула Лейбница для произведения:

Доказательство методом МИ:

49. Теорема Ферма

50. Теорема Дарбу

51. Теорема Ролля

Следствия (будет применяться Теорема Лагранжа, вопрос 53):

52. Теорема Коши, ее геометрический смысл

Следствия:

Геометрический смысл:

53. Теорема Лагранжа, ее геометрический смысл

Геометрический смысл:

54. Теорема Тейлора-Лагранжа. Следствия

Высшая математика. 1 семестр. Билеты 55 - 60 55. Теорема Тейлора – Пеано

Применяется для приблизительного вычисления функции, когда достаточно узнать не величину

погрешности, а только её порядок малости.

0( )

можно ( )

имеет производные до N-го порядка включительно в

. Тогда формулу Тейлора

Пусть

( ) = ∑ =0

(! 0) ( − 0) + [( − 0) ]

→ 0

представить в виде:

( )

( 0)( − 0) +

при

, или:

( − 0)

+ [( − 0)

]

( ) = ( 0) +

( − 0)

+ +

′

"( 0)

( )( 0)

, где

бесконечно малую функцию

[( − 0) ]

называют остаточным членом в форме Пеано.

56. Свойства функций, дифференцируемых в точке до N-го порядка включительно

(

( )

= (

( −1)

( ))

′, где

; ≥ 2

Производная высшего порядка (порядка N):

;

Дифференциал высшего порядка

= ( −1 )

Формула Лейбница: Если функции = ( )

);

и = ( )

раз дифференцируемы, то

( )

= ∑

( )

( − )

– число сочетаний из N элементов по K,

(0)

(

(0)

= ;

)

N-ные

производные элементарных функций:

1.1) ( )( ) =

( )( ) =

(ln ) , > 0

(sin )( )

= sin( + 2 )

(cos )( )

= cos( +

2 )

( )( )

= ( − 1)

( − + 1) −

(ln )( )

= (−1)

( −1)!

−1

57. Вывод формул Тейлора для основных элементарных функций

( ) =

( )

;

( ) = 1 + +

+ +

= {

( ), → 0

(0) = 1

1) = 1 + 1! + 2!2 + + ! + ( )

( )

;

( )

0, = 2

( ) =

= sin( + 2 )

(0) = {(−1) −1, = 2 − 1

sin = −

3! + + (−1) −1 (2 −1)! + ( 2 )

2 −1

(0) = {

(−1) −1, = 2 − 1

( )

= cos( +

;

( )

( ) =

)

0, = 2

cos = 1 − 2!2 + + (−1) (22 )! + ( 2 +1)

( ) = ( + ) : ′( ) = (1 + )

; ( )

( ) = ( − 1) ( − + 1);

( )(0) = ( − 1) ( − + 1)

+ +

+ ( )

(1 + ) = 1 + +

( −1)

( −1)…( − +1)

( − 1)!

( ) = ( + )

′( ) = 1+

( )( ) =

(1+ )

( )(0) = (−1) −1

;

(−1)

( −1)!

;

−1

ln(1 + ) = − 22 + + (−1) −1

+ ( )

58. Вычисление неопределённостей методом выделения главных частей. Пример

функции

( ) = ( − 0) + (( − 0)

) ( )

≠ 0

называют главной частью

В многочлене Тейлора

будет

( )

→ 0

окрестности точки

( )~ ( − 0)

. Тогда, при вычислении предела главная часть функции

эквивалентна всей функции:

при

lim →0

sin = −

6 + ( 3)

Пример:

−sin

1) Разложим по Тейлору

;

2) к обеим частям можно добавить –х: при → 0 − sin = − ( − 63 + ( 3)) , или

− sin = 63

− ( 3),

что эквивалентно выражению − sin = 63;

lim →0

= 6

= 3

3) подставляем:

−sin

59. Три теоремы Лопиталя. Замечания и примеры

Правило0 Лопиталя∞ : Если предел отношения 2-х функций представляет собой неопределённость

вида 0 или ∞, то предел отношения этих функций равен пределу отношения их производных.

( )

Теоремы Лопиталя

( )

( ; )

Пусть

( ; )

( )

′( )

lim → ( ) = lim → ( ) = 0

′( ) ≠ 0

;

( ; )

lim → ′( )

;

Теорема

1: Пусть

определены на

имеют производные на

;

на

; существует

; Тогда

выполняется равенство:

→ ( ) = → ′( )

( )

′( )

= lim → ′( )

Доказательство:

lim → ( ); = lim →

( )− ( +0)

по теореме Коши, где

–

( )

( )− ( +0)

′( )

( < < ) → ′

( )

= → ′( ) ≡ → ′( )

немая переменная

′

( )

′( )

−1 +1

lim →0 ln( + )+ −1

= [1+0−1] = [0] = lim →0

(ln( + )+ −1)′ = lim →0

Пример:

− −

1−1

( −

− )′

+ −

= lim →0 1−1+ (1)

= −1

2+ (1)

Получается такой же ответ, как при решении через ряд Тейлора.

( )

( ;+∞)

( )

′( )

( ;+∞)

( )

= 0

lim →∞

lim →∞ ( ) = lim →∞

′( ) ≠ 0

( ;+∞)

′( )

Теорема 2: Пусть

определены на

;

имеют производные на

;

; Пусть

на

; существует

;

Тогда выполняется равенство:

→∞ ( )

= →∞ ′( )

( )

; →

′( )

limt→0 (1)

limt→0

′(1)(− 12) =

limx→∞ ( )

= =

; =

0 =

Доказательство:

( )

→∞

(1) 1

′(1)(− 12)

= limt→0 ′(1)

= =

= lim →∞ ′

′(1)

′

( )

Пример:

2∙

2 −1

limx→∞ arccos(1−1)

= [0] = limx→∞ (arccos(1−1))′ = limx→∞ −

1∙(− 12)

= limx→∞ (1+(1+ )2)(1+ )2 =

−

(

−

)′

1+(

)

(1+ )

√

√ ( −1)

√ −

√1−

√ −1

limx→∞

(1+ )2

+ 2

= limx→∞

2 2

+2 +1

= limx→∞ 2+2+ 12

= limx→∞

= limx→∞ 2 √1 −

→+∞ ( )

( ) →+∞

( ;+∞)′

( )

( ;+∞)

( ) = ∞

lim

;

( )

= lim

( ) ≠ 0

( ;+∞)

Теорема 3: Пусть

определены на

;

имеют производные на

lim →+∞

′( )

→+∞ ( )

= →+∞ ′( )

;

; пусть

на

; существует

′( )

тогда выполняется равенство:

( )

′( )

Доказательство: Смотри доказательство теоремы 2.

= limx→∞ =

∞ = 0

limx→∞ = [∞] = limx→∞ ( )′

= limx→∞ ∙ −1

Пример:

∞

(ln )′

Примечание: Правило Лопиталя можно применять к пределу несколько раз и комбинировать с другими преобразованиями при необходимости0 ∞ (если даже после других преобразований

остаётся неопределённость вида 0 или ∞).

60. Теорема Штольца. Вычисление

→∞ √ !

. Формула Стирлинга

{ } =1

lim →∞ − −1

∞

Теорема Штольца: Пусть

− −1

∞

бесконечно большие последовательности. Если

существует предел

то существует предел отношения

, равный ему:

lim

= lim

→∞

→∞ − −1

Замечание: Если

– бесконечно большая

возрастающая− −1последовательность, а

последовательность

− −1

} − −1

тоже бесконечно большая и стремится к бесконечности

{

определённого знака{, то

последовательность

{ }

бесконечно большая.

}

! = =

Пример:

lim →∞ √ !

= lim →∞ √

= lim →∞

α = ln(lim →∞

√ !) = lim →∞ (ln √ !) = lim →∞

= lim →∞

−( −1)

= lim →∞

ln !

ln −ln( !)

по TH. Штольца

ln −ln( !)−( −1)ln( −1)+ln(( −1)!)

(ln −ln( −1))+ln( −1)−ln( ( −1)!)+ln(( −1)!)

lim →∞( ln

−1

+ ln( −

1) − ln ) = lim →∞( ln −1

+ ln

−1) = lim →∞

(( − 1) ln −1) =

lim →∞ ( −1)

−1

= lim →∞ (

−1

)

= lim →∞ (1 +

−1)

−1

= 1

, тогда

lim →∞ √ ! = 1

−1+1

−1

Формула Стирлинга

При факториал N можно заменить на эквивалентную функцию:

→ ∞ : !~√2 ∙ ∙ −

Высшая математика. Билеты 61 – 66

( )

61. Критерий постоянства функции. Пример

постоянна на

определена и дифференцируема на промежутке

;

. Эта функция

Пусть функция

( )

= на ;

()

≡ 0 на

; ;

данном промежутке тогда и только тогда, когда её производная на этом же

промежутке тождественно равна 0:

′

Доказательство а)

необходимость: это очевидно, так как

ч ; \{0}

( ) − ( 0)

′( )( − 0)

= 0

зафиксировано и

( ) = По формуле= 0

б)

достаточность:

Пусть

Лагранжа

где с лежит между

√1+ 2−

Пример:

при

′( )

−

2 ∙

2√1+ 2

( ) = − √1+ 2

= 1+ 2

√1−(√

1+ 2

−

∙ (1 +

−

) =

−

≡00

(1+

)√1+

( ) = =?

Пусть1+

. Поэтому

( ) = = (0) = 0 − √1+0 = 0 − 0 = 0

√1+ 2

на R. Следовательно,

≡ √1+ 2

на R.

( )

62.Критерий монотонности функции. Пример

монотонно

определена и дифференцируема на промежутке

;

. Эта функция

Пусть функция

возрастает (убывает) на данном промежутке тогда и только тогда, когда её

производная на этом же промежутке неотрицательна (неположительна):

Доказательство( ) на ;

: а)

′

необходимость( ) ≥ 0 на ; : Рассмотрим( ) наслучай; , когда( )функция≤ 0 навозрастает;

(для

′

. Следовательно,

(; ) и 0

+ ∆ ( ; ),∆ > 0

∆

≥ 0

′(0) = lim∆ →+0

∆

≥ 0;

( 0+∆ )− ( 0)

, тогда

убывающей

функции всё аналогично). Пусть

Лагранжа отсюда 1, 2, ; , 1

< < 2

(2) − (1) = ( )(2

− 1)

(2)

≥ (. 1)

X>0

;

′

по

б) достаточность: Пусть

формуле

> 0

( ) = 2

( ) > 0

Пример

( ) =

′

При

, значит, здесь функция монотонно

′

возрастает (и действительно, мы рассматривали правую ветку обычной параболы, монотонно возрастающую).

63. Необходимый признак точки экстремума

( ) = 0
′
Если функция ( ) дифференцируема в точке с и имеет в этой точке локальный экстремум, то
Доказательство: В точке локального экстремума с функция				не может ни возрастать, ни
убывать. Соответственно, и производная			ни положительной, ни
убывать. Соответственно, и производная	′( )	не может быть( )
отрицательной, то есть ′( ) = 0.	′( )

Геометрический смысл: Если в точке кривой				, соответствующей локальному
экстремуму функции		, существует	касательная к графику		, то эта касательная
	( )			= ( )	= ( )
параллельна оси .

Замечание 1: Это недостаточный признак точки экстремума.

Замечание 2: Функция может иметь экстремум в точке, где её производная не существует.

64. Первый достаточный признак точки экстремума. Примеры

Утверждение: Пусть точка с – точка, подозрительная на экстремум (точка возможного

окрестности

( ) = 0

′

( )

дифференцируема в

( )

экстремума:

′

), а функция

. Тогда, если в пределах этой

производная

меняет знак, то точка с – точка локального экстремума; если

знак не меняется, то

экстремума в этой окрестности нет. То есть если при

< < 2

( )

′

( 1)

∙ :

′( 2) < 0, то экстремум есть, а если ′( 1) ∙ ′( 2)

> 0,

то нет.

справа от с (Нужно доказать, что

–

( )

> 0 (< 0)

слева от с и

( )

< 0 (> 0)

Доказательство Пусть в данной окрестности

′

Лагранжа

( ); 0

≠ , где

лежит

( ) − ( 0)

> 0 (< 0)

при

( ′) − ( ) =

,( )( − 0)

максимальное (минимальное) значение в этой

′

( ) > 0 (< 0)

окрестности). Пусть

′

( )

. Доказать, что

что

> ′

( )

0(> 0)

( ) − ( 0) > 0 (< 0)

знаки, то ( ) > 0 (< 0)

между и

. При

следовательно,

< и 0 > ( ) − ( 0)

. Аналогично доказывается,

если

с обеих сторон от с, то при

имеет разные

есть в этом случае экстремума нет.

Замечание: Порой не получается определить знак производной (смотри пример 2)

Примеры: 1)

( )

= 2

, ′( ) = 2 , X=0 – точка, подозрительная на экстремум.

При

< 0

( )

< 0;

при

> 0

′

( )

> 0;

производная меняет знак, значит, х=0 – точка

′

экстремума (вернее, минимума – вершина обычной параболы).

( ) = {

0, = 0

Здесь вроде 0 – подозрительная точка, но доказать экстремум так не

получится. На самом же деле в точке 0 существует бесконечное множество точек экстремума.

65.Второй достаточный признак точки экстремума. Примеры

Можно использовать, если сложно определить знак производной слева и справа от точки

возможного экстремума с, но легче посчитать вторую производную.

( )

Утверждение: Пусть

точке с конечную вторую производную. Тогда

имеет в

точке максимум, если (" ) имеет

,ви минимум, если

Доказательство: Разложим( 0) < 0

в ряд Тейлора с остаточным( 0) > 0

членом Пеано (первый член -

( ) − ( 0)

= ′( 0)( − 0) +

"( 0)( − 0)2

+ ( − 0)2, → 0

нулевую производную –

переносим сразу влево):

( 0)

Здесь левая часть равна ∆ (∆ ), так как ∆ =2 − 0

, а в правой части ′( 0) = 0 (см. билет 64)

только∆ (∆ ) = 2

( 0)( − 0)

(1 + (1)), → 0

. Видно, что приращение функции зависит

Тогда

от знака 2-й производной, так как остальные множители неотрицательны.

: 1)

( ) = 0

Замечание:

Данная теорема применима не всегда и имеет более узкую сферу действия, чем 1-ая.

Она не работает, если

(2)

или не существует.

(0) = 0

Примеры

( )

+ −

− 2cos

нули функции:

"( )

− − + 2 sin ,

(0)

= 0

, тогда

– точка минимума.

′

( ) =

−

′

– точка, подозрительная на экстремум.

66.+Нахождение+ 2cos

наибольших, (0) = 4 > 0и наименьших= 0

значений функции. Пример

причём

( ) 0 ( ; )

( )

( 0) = 0

= 1,… − 1)

существует

( )

определена, непрерывна и имеет

( ; )

Утверждение: Пусть

N производных на

. Пусть

( 0) ≠ 0

, где

– точка, подозрительная на экстремум и

. Если N=2M (чётное), то в точке

находится либо максимум, либо

минимум. Если же N=2M-1 (нечётное), то экстремума нет.

+ (( − 0) ), → 0

Тейлора – Пеано).∆ (∆ )

= ( ) − ( 0)

= ! ( )( 0) ∙ ( − 0)

(ряд

Доказательство:

При N=2M ∆ (∆ ) = ∙ (21 )! (2 )( 0) ∙ ( − 0)2 + (( − 0)2 ) = (21 )! (2 )( 0) ∙

(

)

(1 + (1)), →

При−

∆ (∆ ) = ∙ 2 1−1)! (2 −1)( 0) ∙ ( − 0)2 −1 + (( − 0)2 −1) = (2 1−1)! (2 −1)( 0) ∙

=2M-1

( − 0)2 −1

(1 +

(1)), → 0

(0) = 8! > 0

точнее –

( )

(0) = 0,

(8)

значит, в нуле есть экстремум (если

Примеры: 1)

минимум, ведь это обычная парабола)

Далее нужно0, = 0

( )

= {

− 12, ≠ 0 Здесь данная теорема не работает, но в нуле будет минимум.

найти точки максимума и минимума, используя материал билетов 63-65.

Впоследствии находится значение максимума (минимума) с помощью подстановки значения

в исходную функцию

( 0)

проверять

;

Замечание: Найденные (максимумы)

(минимумы) – локальные, то есть на рассматриваемом

промежутке

могут быть значения, большие (меньшие)

. Поэтому всегда следует

граничные точки

= и =

(или пределы функции при

→ и →

, если A и B

не входят в промежуток)

67. Достаточный признак выпуклости графика функции

Определение: Функция выпукла вниз (вверх) на интервале, если все точки дуги её графика на этом интервале лежат под (над) соответствующей хордой или на ней (по Фихтенгольцу).

68. Теорема о касательной к графику выпуклой функции

График функции = ( ) имеет на интервале( ; ) ( ; ) выпуклость, направленную вниз (вверх), если график этой функции в пределах лежит не ниже (не выше) любой своей касательной (Лемма 1 по Ильину-Позняку).

Замечание 1: термин «не ниже» имеет смысл, ибо касательная не параллельна оси OY.

Теорема: Если функция = ( ) имеет на интервале ( ; ) конечную вторую производную и если эта производная неотрицательна (неположительна) всюду на этом интервале, то график

функции = ( ) имеет на интервале ( ; ) выпуклость, направленную вниз (вверх).

69. Необходимый признак точки перегиба. Пример

Замечание: этого условия недостаточно, и оно не всегда выполняется.

Пример 2:	= ( ) = 3	; ′( ) = 31	−3	; "( ) = − 29	−3	. Здесь в нуле второй производной не
Пример 2:	1		2		5	. Здесь в нуле второй производной не

существует, однако 0 – точка перегиба.

70. Достаточный признак точки перегиба. Пример

Первый признак:

Второй признак: (если неясен знак второй производной в окрестности с)

Проще"( ) =говоря0 , точка перегиба – это точка, в которой меняется характер выпуклости (то есть или не существует).

		71.Теорема о наклонных асимптотах. Пример
большие функции) при			(. )и ( )				[ ; +∞)		( ( ) ас̿ ( ))
	б.м.ф. (	→ +∞			определены на				( ( ) ас̿ ( ))
Определение: Пусть функции					определены на			и они – б.б.ф. (бесконечно
( ) − ( ) =						→ +∞				→ −∞	, если
				Тогда эти функции асимптотически равны							, если
	бесконечно малая функция) при						. Аналогично и с				.

= +

= ( )

= (1)при → ∞

Нахождение( ) ас̿ ( +наклонной) →асимптоты+∞

: → −∞

( ) − ( + )

Прям я

– асимптота функции

, если они асимптотически равны:

при

(или

) или

→∞

→∞ ( )

Пример: ( ) = √ 2

− 5 +

= lim

;

= lim

[ ( ) − ]

→∞

√ 2

− 5 + 3

→∞ √

5 32

lim

= lim

1 −

= 1;

= lim

− 5 + 3 − 1 ∙ = lim

− 5 + 3 − 2

= lim

√

−5 + 3

√

− 5 + 3 +

− 5 + 3 + = lim

→∞ √

→∞

−5 +

⁄

= lim

;

= − 2

→∞

Наклонная асимптота: = − 25

Следует отдельно упомянуть вертикальную асимптоту:

−5 + 3 2

72. Общая схема исследования функции и построения( ) = ⁄ её−графика( − ) по⁄ характерным точкам на примере функции

( ) =

− ( − 1)

( ) =

I. Найти область определения функции, область значений, чётность функции.

2⁄3

1⁄3:

− 1)

- непрерывная функция, х принимает любые

(− ) = (− )

2⁄3

− ((− )

1⁄3

2⁄3

− (

− 1)

1⁄3

= ( )

– чётная функция;

значения;

следовательно, можно рассмотреть только положительную часть (

), зная, что

lim ( ) =

lim

− (

− 1)

lim

−

(1 − )

= Тейлор

отрицательная ей симметрична.

2⁄3

1⁄3

≥ 0

→+∞

2⁄3

1⁄3

→+∞

−

)) =

lim

(1 − 1 + 3

− (

))

lim

2⁄3

(1 − 3

+ (

2⁄3

→+∞

lim

−4⁄3

(

− (1)) = 0

– ложное

( ) = 0 ↔

→+∞

= (

− 1)

↔

− 1

2⁄3

− (

− 1)

1⁄3

= 0 ↔

2⁄3

1⁄3

высказывание, тогда

, то есть функция сохраняет знак (и имеет место горизонтальная

(1) = 12⁄3 − (1 − 1)1⁄3

= 1 − 0 = +1

– функция строго положительна:

( ) > 0

асимптота у=0)

для

определения знака возьмём х=+1:

( ) ≠ 0

(Кстати, график функции проходит через точку (1;1))

II.Найти первую производную от функции, её область определения, определить точки

′( ) = ( 2⁄3 − ( 2

− 1)1⁄3)′ =

−3

− 1

( 2

− 1)−2⁄3

∙ 2 = 2 ( −3 − ( 2 − 1)−2⁄3)

экстремума (или точки, подозрительные на экстремум).

( ) = +\{0}\{1} (если

′( ) = 0 ↔ −3

рассматривать только неотрицательную часть)

↔ −2 2 + 1 = 0

= ( 2 −

1)−2⁄3

↔ ( 2

− 1)2⁄3

= 3

↔ ( 2

−

1)2

= 4

= √12 (= √22) – точка максимума (в ней производная меняет знак с + на -).

1 3

2⁄3

(√2) = (2)

− (2

− 1)

√2 + √2 = 3√2

= 2 =

√4

Теперь рассмотрим внимательнее точку х=0.

(

− 1)

) =

√

(1 − √

)

– на + (меняется только

−3

(1 −

4⁄3

−2⁄3

√

(

При переходе через неё функция

меняет знак с

В(0)нашем= 0 случае− (0 −

1⁄3

значит3

, х=0 – точка локального минимума3 .

−1

(касательная в этой точке параллельна Оу (х=0)

точку1)

=х=1,1

где производная не существует, надо исследовать дальше с

помощью 2-й производной.

III. Найти вторую производную от функции, её область определения, определить точки

перегиба (при необходимости уточнить точки экстремума).

]

( ) = 3 [− 3

−4⁄3

(

− 1)

−5⁄3

∙ 2

−

(

− 1)

−2⁄3

3( 2

− 1) 4⁄3]

−4⁄3( 2

−

1)−5⁄3[−( 2

− 1)5⁄3

+ 4 10⁄3 −

"( )

( ) = +\{1}

↔ 4( 2 + 3) = ( 2

− 1)5

= 0 ↔ 4⁄3(4 2

− 3 2 +

= ( 2

− 1)5⁄3

10 + 9 8

+ 27 6

+ 27 4

= 10

− 5 8 + 10 6 − 10 4 + 5 2

− 1

больше 0;

+ 17

+ 37

− 5

+ 1 = 0

: первые 2 члена с чётной степенью, то есть

Точки перегиба:

оставшиеся члены образуют биквадратное уравнение с отрицательным дискриминантом, тоже больше 0. Тогда вторая производная не равна нулю.

Однако у нас есть( 2точка− 1)5х⁄=1,3 где 2-я производная не существует. Поскольку при прохождении

через эту точку меняет знак, а другие части нет, то и вся вторая производная меняет знак, тогда х=1 – точка перегиба. Мы уже знаем её координаты (1; 1) То, что первая производная в этой точке не существует, означает лишь, что касательная к графику в этой точке параллельна оси Оу (её уравнение х=1).

IV. По полученным результатам построить график функции (сначала отметить

стационарные точки и точки перегиба; затем провести в этих точках касательные к кривой; в конце провести схематически саму кривую).

В нашем случае начнём с положительной половины графика (функция чётная). Мы имеем:

Минимум

(0; 1)

(

= 0

√2

(касательная

);

= 1

(1; 1)

);

Максимум

( 2

касательная

);

Перегиб

касательная

;(√4)

= √4

Асимптота

Получаем:

= 0

Общий вид графика целиком:

<<< < Предыдущая 1 2 3 45 / 55

Соседние файлы в папке билеты 1 сем

#
17.01.20201.32 Mб8019-36.docx
#
22.12.20193.56 Mб4737-54.docx
#
22.12.201938.41 Кб3755-60.docx
#
22.12.201932.86 Кб3961-66.docx
#
18.01.20201.33 Mб2967-72.docx
#
18.01.20206.68 Mб81все вместе.pdf