Найдём левый односторонний предел:

Правый и левый односторонний пределы существуют и равны 1, а значит и сам п редел равен 1.

29. Теорема о разности эквивалентных бесконечно малых и о замене на эквивалентные в пределах.

Предел отношения двух бесконечно малых функций не изменится, если каждую или одну из них заменить эквивалентной ей бесконечно малой.

Теорема. Разность двух эквивалентных бесконечно малых функций есть бесконечно малая более высокого порядка, чем каждая из них.

Справедливо и обратное утверждение: если разность б.м.ф. α и ß есть бесконечно малая высшего порядка, чем α или ß, то α и ß — эквивалентные бесконечно малые.

Действительно, так как

т. е. Отсюда т. е. α~ß.

Аналогично, если то α~ß.

Теорема о замене функции на эквивалентную под знаком предела

Под знаком предела

числитель или знаменатель можно заменить на эквивалентные.Доказательство. Пусть в точкех = х0имеемf(x) ~ α(x). В этом случае

,

что и требовалось доказать.

При .

30. Понятие о порядке и главной части функции. Примеры. Запись замечательных пределов в разных видах.

Выделение главной части функции - мощный приём при решении задач на вычисление пределов. Основная цель выделения главной части - получение

более простой функции, которая в окрестности предельной точки ведёт себя также, как исходная громоздкая. Тогда по теореме 2 о замене бесконечно малых на эквивалентные мы можем заменить громоздкие функции в числителе и знаменателе на эквивалентные простые); основной инструмент при выделении главных частей - табл. эквивалентных бесконечно малых.

Как следует из определений, утверждения "при ха

1.f(x)~g(x);

2.f(x)-g(x)=o(g(x)) =o(f(x));

3.g(x) есть главная часть f(x)" эквивалентны.

Так как для f(x) может существовать бесконечно много главных частей

при ха (например, при х0 ~ ~ ~ ~ ~ ~ …..),

при выделении главных частей указывается их вид; при решении задач на вычисление пределов при ха обычно это С0(х-а)k для бесконечно малых

и для бесконечно больших, при х¥ - это для бесконечно малых

и для бесконечно больших, где С0 = const¹0, k =const>0 – порядок малости или роста функции f(x) относительно функции (х-а) (или

относительно при х¥). Для главных частей такого вида бесконечно малых при ха функций равносильны следующие утверждения:

1. ;

2. , где a(х) – БМ при х®а;

3. ;

4. , где ;

f(x) ~ .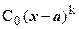

Таким образом, в простейших случаях рецепт для выделения главной части вида С0(х-а)k БМ при ха функции f(x) состоит в следующем: f(x) надо

представить в виде f(x)= , где .

Тогда , и - главная часть функции f(x) при ха.

Аналогично изложенному выше, с заменой (х-а)k на , формулируются

утверждения и правило для выделения главной части функции, бесконечно малой при х¥.

Рассмотрим ряд примеров на выделение главной части и определение порядка малости функций (в скобках указываются применённые формулы табл. экв.):

1. . Представим f(x) в виде .

Если , то , поэтому , k=1 – порядок малости f(x) при х0.

порядок малости f(x) при х0.

31.Определение и свойства непрерывных функций.

Определение 1. Функция называется непрерывной в точке a, если она удовлетворяет следующим трём условиям:

1) определена в точке а (то есть существует );

2) имеет конечный предел функции при ;

3)этот предел равен частному значению функции в точке а, то есть .

Определение 2. Функция называется непрерывной справа (слева) в точке a, если правое (левое) предельное значение этой функции в точке a существует и

равно частному значению .

Определение 3. Функция называется непрерывной в точке а, если она определена в этой точке и бесконечно малому приращению аргумента

соответствует бесконечно малое приращение функции: .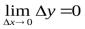

Определение 4. Точки, в которых функция не обладает свойством непрерывности, называются точками разрыва функции.

Определение 5. Функция непрерывна на множестве , если она непрерывна в любой точке. Функция непрерывна на интервале или на сегменте , если

; .

Свойство 1: (Первая теорема Вейерштрасса). Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке [a, b] выполняется условие –

M f(x) M.

Доказательство этого свойства основано на том, что функция, непрерывная в точке х0, ограничена в некоторой ее окрестности, а если разбивать отрезок [a, b] на бесконечное количество отрезков, которые “стягиваются” к точке х0, то образуется некоторая окрестность точки х0.

Свойство 2: Функция, непрерывная на отрезке [a, b], принимает на нем наибольшее и наименьшее значения.

Т.е. существуют такие значения х1 и х2, что f(x1) = m, f(x2) = M, причем

m f(x) M

Отметим, эти наибольшие и наименьшие значения функция может принимать на отрезке и несколько раз (например – f(x) = sinx).

Разность между наибольшим и наименьшим значением функции на отрезке называется колебанием функции на отрезке.

Свойство 3: (Вторая теорема Больцано – Коши). Функция, непрерывная на отрезке [a, b], принимает на этом отрезке все значения между двумя произвольными величинами.

Свойство 4: Если функция f(x) непрерывна в точке х = х0, то существует некоторая окрестность точки х0, в которой функция сохраняет знак.