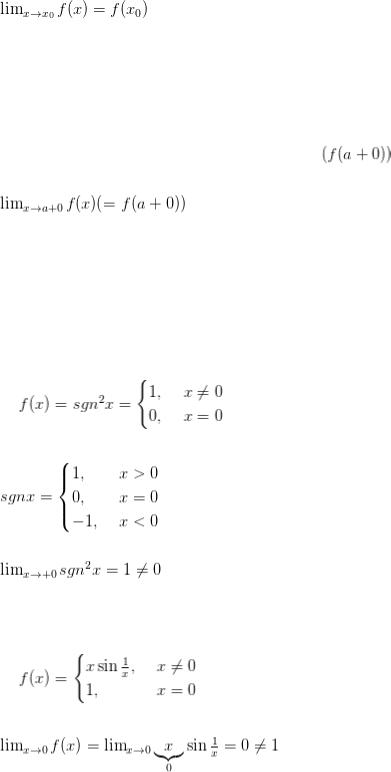
Точки в которых функция не является непрерывной называется точкой разрыва.

Классификация точек разрыва.

Определение:

Если существует конечный предел справа

и,

причём 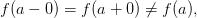то точка называется точкой устранимого разрыва.(название устранимый, оправдывает себя), его можно устранить изменив значение функций в точке .

Пример

1)

точка 0-точка устранимого разрыва.

2)

точка устранимого разрыва.

Определение:

Если существуют конечные односторонние пределы

и , то точка называется точкой разрыва первого рода.

Примеры

1)

2)

Определение:

Точка называется точкой разрыва второго рода, если она не является точкой разрыва первого рода и точкой устранимого разрыва, то есть если хотя бы один из сторонних пределов либо не существует, либо бесконечен.

Пример

точка разрыва второго рода.

33. Теоремы Коши о промежуточном значении функции. Следствие.

Теорема 1(первая теорема Больцано-Коши). Пусть функция определена и непрерывна на отрезке () и на концах его принимает значения

разных знаков ( ). Тогда найдется такая точка , в которой функция обращается в нуль:

(1)

Д о к а з а т е л ь с т в о. Для определенности будем считать, что

(2)

Разделим отрезок на два средней его точкой . Тогда либо в этой точке имеет место равенство (1), либо на концах одного (и только одного) из отрезков

(3)

,,

функция будет принимать значения разных знаков, причем, в силу (2), отрицательное значение – на левом конце и положительное – на правом.

Обозначив эту половину отрезка через .Таким образом, будем

иметь:

. (4)

Разделим теперь пополам отрезок . Тогда опять-таки, либо в

точке имеет место равенство (1), либо на концах одной из его

половин функция принимает значения разных знаков. Обозначим через ту из этих половин, для которой

(5)

Продолжая описанный процесс деления отрезков пополам и далее, либо через конечное число шагов мы обнаружим, что в точке деления очередного отрезка функция обращается в нуль и тем самым завершим доказательство теоремы, либо получим бесконечную последовательность вложенных друг в друга

отрезков , длины которых стремятся к нулю при ,

(6)

при этом на концах каждого из этих отрезков функция принимает значения разных знаков, а именно,

(7)

По лемме о вложенных отрезках рассматриваемые отрезки имеют единственную общую точку , при этом

(8)

Тогда переходя в неравенствах (7) к пределу при , с учетом непрерывности функции на отрезке и, в частности, непрерывности ее в точке , получим

и, следовательно, , причем из неравенств (2) следует, что □

Замечание 1.Для непрерывной на некотором отрезке функции , принимающей в каких-то двух точках этого отрезка значения разных знаков,

доказанная теорема очевидно доставляет метод приближенного отыскания

корней уравнения . Этот метод часто называют методом деления отрезка пополам.

Замечание 2.Теорема 1 позволяет также установить наличие вещественного корня у всякого многочлена нечетной степени

Действительно, при достаточно больших по абсолютной величине значениях этот многочлен имеет знак старшего члена, т.е. члена .

Точнее, при положительных таких он имеет знак, равный знаку 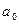, а при отрицательных таких он имеет обратный знак. Так как многочлен – непрерывная на всей числовой оси функция, то по теореме 1 хотя бы в одной

точке он обращается в нуль.

Теорема 2 (вторая теорема Больцано-Коши). Пусть функция определена и

непрерывна на отрезке , причем на концах этого отрезка она принимает разные значения

.

Тогда каковы бы ни было число , лежащее между и найдется такое , что

.

Д о к а з а т е л ь с т в о. Пусть для определенности . Выберем произвольное , , и рассмотрим вспомогательную

функцию . Она, очевидно, непрерывна на отрезке и на его концах принимает значения разных знаков:

.

По теореме 1 существует такое , что , т.е. или □

Следствие. Если функцияопределена и непрерывна на конечном или

бесконечном промежутке , то множество ее значений также

есть некоторый промежуток.

Д о к а з а т е л ь с т в о. Пусть Выберем произвольное . Из определения точных граней следует, что найдутся такие значения и (), что

По теореме 2 существует число , лежащее между и , такое, что . В силу произвольности выбранного это означает,

что . С учетом определения чисел и отсюда следует, что множество есть некоторый промежуток □

34. Теоремы Вейрштрасса о непрерывности функций. Следствие. Контрпример.

Теорема 1(первая теорема Вейерштрасса). Всякая непрерывнаяна отрезке функция ограничена на этом отрезке.

Д о к а з а т е л ь с т в о. Предположим противное. Тога для любого натурального найдется такая точка , что

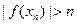. (1)

Так как последовательность ограничена (), то по теореме Больцано-Вейерштрасса она содержит сходящуюся

подпоследовательность . Пусть

при .

Очевидно, что (для того, чтобы убедиться в этом достаточно в неравенствах перейти к пределу при ). Поэтому в силу непрерывности функции на отрезке

Следовательно, последовательность ограничена, что, противоречит тому, что согласно (1) □

Пусть функция определена на множестве . Далее вместо символов и , служащих для обозначения точных верхней и

нижней граней множества значений функции на множестве часто будем использовать символы

и 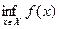, соответственно.

Теорема 2(вторая теорема Вейерштрасса). Всякая непрерывнаяна отрезке функция достигает на нем своих точных верхней и нижней граней, т.е.существуют такие точки ,что

, .

Д о к а з а т е л ь с т в о. Докажем, например, утверждение теоремы относительно точной верхней грани. Доказательство проведем от противного.

А именно, положим и предположим, что

.

Тогда, очевидно, функция

будет непрерывной на отрезке . Поэтому по теореме 1 она будет ограниченной на этом отрезке. В частности, найдется такое , что