
Билеты. Высшая математика.
1)Свойства действительных чисел.
N – множество натуральных чисел (1,2,…,+∞)
Z – множество целых чисел (-∞,+∞)
Q – множество рациональных чисел ( ) , q Z, p Z
R – множество действительных (вещественных) чисел; множество всевозможных, бесконечных десятичных дробей
Вещественные числа, не являющиеся рациональными, называют иррациональными.
|
|
b , b c a c |
транзитивное свойство знака ) |
|||||
a |
||||||||
|
, имеет место( |
одно и только одно из соотношений: = , < , > |
||||||
> |
|
существует m |
|
, такое что |
|
(аксиома Архимеда) |
||
|
> → > |
|
|
< |
> |
|||
|
|
|
|
|
||||
a+b комутативная группа по сложению
Комутативность: a+b=b+a
Ассоциативность: a+(b+c)=a+b+c
Наличие нейтрального члена: a+0=0+a=a
Наличие< противыполняетсяожного члена+ : a+b=1;< + b=-a
a*b комутативная группа по умножению
|
Комутативность: a*b=b*a |
|
Ассоциативность: a*(b*c)=a*b*c |
|
Наличие нейтрального члена: a*1=1*a=a |
|
< + выполняется < |
|
Наличие противоположного члена: a*b=1; b=1/a |
, , сложение дистрибутивно относительно умножения
( + ) = +
R – плотное множество. Между любыми двумя различными числами a и b существует бесконечное множество действительных
чисел.
Пусть A и B — два непустых множества в R таких, что a A b B a ≤ b, т. е. любой элемент A не больше любого элемента B. Тогда c R | a A b B a ≤ c ≤ b, т.е. найдется хотя бы одно число, разделяющее A и B
2)Свойства абсолютной величины действительного числа
Абсолютной величиной (модулем) действительного числа х (обозначается │х│) называется неотрицательное действительное число, удовлетворяющее
условиям:
│х│ = х ,если х ≥ 0; │х│ = −х ,если х ≤ 0
Свойства:
1)Абсолютная величина алгебраической суммы нескольких действительных чисел не больше абсолютных величин слагаемых:
│a+b│≤│a│+│b│
2)Абсолютная величина разности не меньше разности абсолютных величин уменьшаемого и вычитаемого: │a-b│≥│a│-│b│ (│a+b│≥│a│-│b│)
3)│ab│≤│a││b│
4)│a/b│≤│a│/│b│
Докозательство: сложим почленно неравенства −│a│ ≤ a ≤ │a│ и −│b│ ≤ b ≤ │b│
−(│a│ + │b│) ≤ a + b ≤ │a + b│ и получаем │a+b│≤│a│+│b│; если заменить b на –b то получим│a-b│≤│a│+│b│
1
3)Ограниченные множества и их границы. Понятие счетного и несчетного множества. Примеры.
Если каждому числу п натурального ряда чисел 1,2,... n, ... ставится в соответствие по определенному закону некоторое вещественное число xn то множество занумерованных вещественных чисел x1,x1,...,xn,… мы и будем называть числовой последовательностью или просто последовательностью.
Доказательство. Пусть {хт} — сходящаяся последовательность и а — ее предел. Тогда, существует ε, N(ε): 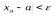 при
при ,
, 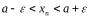 ,
,
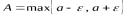 . Тогда
. Тогда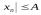 для
для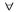 n.
n.
2
5)Теорема о предельном переходе в неравенстве.
Теорема: Если элементы сходящейся последовательности {хn}, начиная с некоторого номера, удовлетворяют неравенству хn ≥b(хn ≤ Ь), то и предел а этой последовательности удовлетворяет неравенству а≥b (а≤b).
Доказательство: Пусть все элементы xn, начиная с некоторого номера, удовлетворяют неравенству Хn ≥ Ь. Требуется доказать неравенство а ≥Ь. Предположим, что а < Ь. Поскольку а — предел последовательности {xn}, то для положительного ε = Ь — а можно указать номер N такой, что при n≥ N выполняется неравенство \хп — а\ < Ь — а. Это неравенство эквивалентно следующим двум неравенствам: — (Ь — а) < хп — а < Ь — а. Используя правое из этих неравенств, получим хn < Ь, а это противоречит условию теоремы.
|
|
lim →∞ = 0 |
|
Замечание. Элементы сходящейся последовательности {хn} могут удовлетворять строгому неравенству хn > b, однако при этом предел а может |
|||
оказаться равным b. Например, если хn = |
1, то хn > 0, однако |
|
. |
Следствие 1. |
Если элементы хn и уn сходящихся последователъностей {хn} и {уn}, начиная с некоторого номера, удовлетворяют неравенству хn , уn, то их |
пределы удовлетворяют такому же неравенству: lim →∞ ≤ lim →∞ . |
|
Следствие 2. |
Если все элементы сходящейся последовательности {хn} находятся на сегменте [а,Ь], то и ее предел с также находится на этом сегменте. |
6)Теорема о сжатой переменной (о трех последовательностях)
Теорема: Пусть {хn} и {zn} — сходящиеся последовательности, имеющие общий предел а. Пусть, кроме того, начиная с некоторого номера, элементы последовательности {уn} удовлетворяют неравенствам хn ≤ уn ≤ zn. Тогда последовательность {уn} сходится и имеет предел а.
Доказательство. Достаточно доказать, что последовательность {уn — а} является бесконечно малой. Обозначим через N* номер, начиная с которого |
|
|||||||||
|
|
то для любого ε> 0 можно указать номера N и N такие, что при |
≥ |
ε, а при n≥ N |
— а |
< ε. Пусть N = |
|
lim →∞ = |
|
|
выполняются неравенства, указанные в условии теоремы. Тогда, начиная с этого же номера, будут выполняться также неравенства хn |
— а ≤уn — а ≤zn-a. |
|||||||||
lim →∞ = |
|
|
|
|
|
|
|
|
|
|
Отсюда следует, что при n ≥ N* элементы последовательности {yn — a} удовлетворяют неравенству │yn –a │≤max{│xn -a│,│zn-a│}.Так как |
|
и |
||||||||
|
, |
1 |
2 |
n N1 \xn - a\ < |
2 \zn |
\ |
|
max{N*, N1, N2}. |
|
|
Начиная с этого номера, имеет место неравенство \уп ^ а\ < ε. Итак, последовательность {уn –а} — бесконечно малая. Теорема доказана:) |
|
|||||||||
7)Теорема о стабилизации знака. |
|
> ( < ) |
|
|
|
|
|||||||
xn |
> ( < ) |
. |
|
|
|
|
|
|
|
|
|
|
|
Теорема: Пусть {xn} сходящаяся последовательность , предел которой равен а; а |
. Тогда начиная с некоторого номера n , переменная |
|
|||||||||||
Докозательство:Пусть |
|
. Предположим ε=a-p . По определению предела последовательности для этого ε найдется Кε |
|
N такое, что К Кε и│хк-а│ ε. |
|||||||||
|
|
|
ε |
|
число хк удовлетворяет неравенствам а-ε |
хк а+ε. Но а-ε=а-(а-р)=р, значит, К |
Кε и р хк . Предположим Кр = Кε . Тогда при всех К |
Кр |
|||||
Т.е при любых К К , |
|
< |
|
< < |
> |
< |
|
> |
< |
||||
справедливо p<>k |
|
Ч.и.т.д |
|
|
|
> |
|||||||
|
|
x |
. |
|
|
|
|
|
|
|
|
|
|
8)Теоремы о бесконечно малых.
Теорема: Сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность.
Доказательство. Пусть {аn} и {bn} — бесконечно малые последовательности. Докажем, что последовательность {an +bn}— бесконечно малая. Пусть ε — произвольное положительное число, N1— номер, начиная с которого \аn\ < ε/2, а N2 — номер, начиная с которого \bn\ < ε/2. (Такие номера N1 и N2
найдутся по определению бесконечно малой последовательности.) Так как модуль суммы двух чисел не превосходит суммы их модулей, т. е.
\аn+ bn\ ≤\аn\ + \bn\ , то, обозначив через N наибольший из двух номеров N1 и N2, мы получим, что, начиная с номера N, выполняется неравенство \аn + bn\ < ε. Это означает, что последовательность {аn + bn} бесконечно малая. Теорема доказана.
Теорема: Разность двух бесконечно малых последовательностей есть бесконечно малая последовательность.
Эта теорема доказывается аналогично предыдущей, только вместо неравенства \аn + bn\ ≤ |аn| + \bn\ следует взять неравенство \аn — bn\≤\аn\ + \bn\.
Следствие. Алгебраическая сумма любого конечного числа бесконечно малых последовательностей — бесконечно малая последовательность.
Теорема: Бесконечно малая последовательность ограничена.
Доказательство. Пусть {аn} — бесконечно малая последовательность и ε - некоторое положительное число. Пусть, далее, N — номер, начиная с которого \аn\ < ε. Обозначим через А наибольшее из следующих N чисел: ε, |a1|, |а2|,..., │aN -1│.Это можно записать так: А = mах{ε, |a1 |, |a2|,…, |aN -1|} . Очевидно, \а2\ ≤А для любого номера n , что означает ограниченность последовательности. Теорема доказана.
3
Теорема: Произведение ограниченной последовательности на бесконечно малую последовательность представляет собой бесконечно малую последовательность.
Доказательство. Пусть {хn} — ограниченная , а {an} — бесконечно малая последовательности. Так как последовательность {хn} ограничена, то существует число А > 0 такое, что любой элемент хn удовлетворяет неравенству \хn\ ≤А. Возьмем произвольное положительное число ε. Поскольку последовательность {аn} бесконечно малая, то для положительного числа ε/А можно указать номер N такой, что при n≥N выполняется неравенство \an\ < ε/А. Тогда при n≥ N \ хn*an\ = \хn\ * \аn\ < А = ε. Поэтому последовательность {хn * аn} бесконечно малая. Теорема доказана.
Следствие. Произведение любого конечного числа бесконечно малых последовательностей представляет собой бесконечно малую последовательность.
Замечание. Частное двух бесконечно малых последовательностей может быть последовательностью любого типа и даже может не иметь смысла.
Теорема. Если все элементы бесконечно малой последовательности {аn} равны одному и тому же числу с, то с = 0.
Докозательство: Пусть 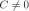 . Тогда для
. Тогда для 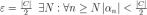 . По условию,
. По условию,  , тогда
, тогда 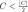 . Получили противоречие, следовательно,
. Получили противоречие, следовательно,  .
.
9)Теоремы об арифметических действиях над сходящимися последовательностями.
Теорема . Сумма сходящихся последовательностей {хn} и {уn} есть сходящаяся последовательность, предел которой равен сумме пределов последовательностей {хn} и {уn}.
Доказательство. Пусть а и b — соответственно пределы последовательностей {хn} и {уn}. Тогда хn = а + аn и yn = Ь + bn, где {аn} и {bn} — бесконечно малые последовательности. Следовательно, (хn + уn) - (а + Ь) = аn + bn. Таким образом, последовательность {(хn+уn) — (а+Ь)} бесконечно малая, и поэтому последовательность {хn + уn} сходится и имеет своим пределом число а + Ь.
Теорема . Разность сходящихся последовательностей {хn} и {уn} есть сходящаяся последовательность, предел которой равен разности пределов последовательностей {хn} и {уn}.
Доказательство этой теоремы аналогично доказательству теоремы о сумме.
Теорема 3.11. Произведение сходящихся последовательностей {хn} и {уn} есть сходящаяся последовательность, предел которой равен произведению пределов последовательностей {хn} и {уn}.
Доказательство. Если а и b — пределы последовательностей {хn} и {уn} соответственно, то хn = а + аn, уn = b + an и хn * yn = а*b + а*bn + b*an +anbn. Следовательно, хn * уn - а *b = а*bn + b*an +anbn. В силу теоремы о бесконечно малых и следствия из нее, { а*bn + b*an +anbn } бесконечно малая, т. е. и последовательность {хп - уп — а - Ь} бесконечно малая, и поэтому последовательность {хп • уп} сходится и имеет своим пределом число а • Ь.
Лемм1 } а . Если последовательность {уn} сходится и имеет отличный от нуля предел Ь, то, начиная с некоторого номера, определена последовательность {уn , которая является ограниченной.
Доказательство. Пусть е = | Ь |/2. Так как b≠0, то е > 0. Пусть N — номер, соответствующий этому е, начиная с которого выполняется неравенство | уn — |
|||
|
{ |
|
уn │ │ |
b│ < е или │yn -Ь│ < │Ь│/2. Из этого неравенства следует, что при n≥N выполняется неравенство │уn│> │Ь│/2. Поэтому при n≥N имеем │ 1 │< 2 . |
|||
Следовательно, начиная с этого номера N, мы можем рассматривать последовательность |
|
1 |
и эта последовательность ограничена. Лемма 1 |
доказана. |
|
уn} |
|
Теорема. Частное двух сходящихся последовательностей {хn} и {уn} при условии, что предел {уn} отличен от нуля, есть сходящаяся последовательность, предел которой равен частному пределов последовательностей {хn} и {уn}.
Доказательство. Из доказанной леммы 1 следует, что, начиная с некоторого номера N, элементы последовательности {уn} отличны от нуля и |
||||||||||||||||||||||||||
последовательность { |
1 |
ограничена. Начиная с этого номера, мы и будем рассматривать последовательность { |
|
. Пусть а и b — пределы |
||||||||||||||||||||||
|
|
|
|
|
|
n |
} и {у |
n}. |
Докажем, что последовательность{ |
|
|
|
как хn = а + an , уn = b +bn |
|||||||||||||
последовательностейу{nх} |
1 |
|
− |
бесконечно малая. В самом деле, такуn |
} |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
− |
|
|
|
|
|
Так как |
|
|
1} |
|
|
|
|
|
|
||||||
|
уn |
|
|
|
|
{ |
|
уn |
) |
} |
|
} |
|
последовательностьуn |
|
уn |
|
|
|
|
|
|
|
|||
то |
|
|
|
|
|
у1n |
( − |
{уn − |
|
|
ограничена, а последовательность |
|
|
|
|
|
бесконечно малая, то |
|||||||||
|
|
|
|
|
|
|
= |
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||||
последовательность |
|
|
|
|
|
|
|
|
|
|
|
|
{ |
|
|
|
|
|
|
|
|
|||||
|
|
− |
|
= |
|
|
|
|
|
|
( −≡ |
) |
|
бесконечно малая. Теорема}доказана. |
{ − |
|
} |
|
||||||||
10)Теорема Вейештрасса о последовательностях.
*Определение. Последовательность {хn} называется неубывающей (невозрастающей), если каждый последующий член этой последовательности не меньше (не больше) предыдущего, т. е. если для всех номеров n справедливо неравенство xn ≤xn+1 (xn ≥xn+1 ). Монотонные последовательности
ограничены либо сверху, либо снизу. Именно: невозрастающие последовательности ограничены сверху, а неубывающие последовательности ограничены снизу своими первыми элементами. Поэтому невозрастающая последовательность будет ограниченной с двух сторон, если она ограничена снизу, а неубывающая последовательность будет ограниченной с двух сторон, если она ограничена сверху.
4
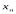
*Теорема . Если неубывающая (невозрастающая) последовательность {хn} ограничена сверху (снизу), то она сходится.
Замечание 1. Условие ограниченности монотонной последовательности представляет собой необходимое и достаточное условие ее сходимости.
Теорема Вейерштрасса об ограниченной сверху возрастающей последовательности (или ограниченной снизу убывающей последовательности) утверждает, что любая ограниченная сверху монотонно возрастающая (или ограниченная снизу монотонно убывающая) последовательность имеет предел, причем этот предел равен её точной верхней (или нижней) грани.
Пусть |
lim →∞ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> 0 |
|
|
|
|
|
|
|
< |
||||
{xn} - ограниченная возрастающая последовательность. Cледовательно, по теореме о супремуме, имеет супремум. Обозначим его через S. |
|||||||||||||||||||||||||||||||||
11) |
|
|
> |
|
< |
|
|
|
|
|
|
|
< ε |
|
> |
|
|
|
|
|
lim →∞ = . |
|
|
|
|
|
|
|
|
|
|||
Тогда |
|
|
|
. Действительно, так как S — супремум множества |
{xn}, то для любого ε |
|
существует номер N такой, что S-ε N≤S. Тогда для |
||||||||||||||||||||||||||
любого n |
|
имеем: S-ε N≤xn≤S. Тогда │xn-S│ |
|
при n |
|
. Следовательно, |
|
|
Теорема доказана. |
|
|
|
|
||||||||||||||||||||
|
Определение числа е как предела последовательности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Применим теорему Вейерштрасса о существовании предела монотонной последовательности для доказательства существования предела |
|||||||||||||||||||||||||||||||||
последовательности {xn}, элемент хn которой определяется формулой = (1 + 1) . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Докажем, что эта последовательность возрастает и ограничена сверху. Применив формулу бинома Ньютона, найдем |
1 |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
= 1 + 1 |
+ ( − 1) |
12 + ( − 1)( − 2) |
13 + + ( − 1)( − 2) …[ − ( − 1)] |
|
|
||||||||||||||||||||||
Представим это выражение в следующей |
форме: |
2! |
|
|
|
3! |
|
|
|
|
|
|
|
! |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
1) |
= 2 + |
2!1 (1 − 1) + 3!1 |
(1 − |
1)(1 − 2) + + 1! (1 − 1)(1 − 2) …(1 − −1). |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Аналогично запишем элемент xn+1 |
: |
(1 − |
|
1 |
) + 1 |
(1 − |
|
1 |
)(1 − |
2 |
|
) + + |
1 |
(1 − |
1 |
)(1 − |
2 |
)… (1 − |
|
). |
|||||||||||||
|
|
|
|
|
( + 1) = 2 + 1 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
2! |
|
x |
|
+ 1 |
|
3! |
|
+ 1 |
|
+ 1 |
|
( + 1)! |
|
|
+ 1 |
|
+ 1 |
|
|
+ 1 |
|
|||||
Сравнивая два выражения получаем , что |
|
n< |
|
n+1 |
|
т.е. последовательность |
|
n |
возрастающая. |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
, |
|
|
|
|
|
|
{x } |
|
|
|
|
|
|
|
|
|
|
||
Для доказательства ограниченности1 < этой1 последовательности сверху заметим, что каждое выражение в круглых скобках в соотношении 1) меньше
единицы. Учитывая также, что ! 2 −1 , при к ≥2 получим
< 2 + 12 + 212 + + 2 1−1 = 3 + 2 1−1 < 3.
Итак, последовательность {x } возрастает и ограничена сверху. По теоремеlim Вейерштрасса(1 + 1) последовательность {x } имеет предел. Этот предел по
определению называют числом . Следовательно по определению = e. (e =2,71828)
n е →∞ n
12)Критерий сходимости последовательностей, основанный на поведении их подпоследовательностей. Лемма о вложенных промежутках.
Определение . Последовательность  , которая составлена из членов последовательности
, которая составлена из членов последовательности и в которой порядок следования её элементов совпадает с их порядком следования в исходной последовательности
и в которой порядок следования её элементов совпадает с их порядком следования в исходной последовательности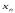 , называется подпоследовательностью этой последовательности.
, называется подпоследовательностью этой последовательности.
Лемма о вложенных промежутках (Теорема Кантора-Коши?). Для всякой системы вложенных отрезков [an,bn] … [a2,b2] [a1,b1]lim существует( − )хотя= 0 бы одна точка c, принадлежащая всем отрезкам данной системы. Если, кроме того, длина отрезков системы стремится к нулю: →∞ то c — единственная общая точка всех отрезков данной системы.
Доказательствоlim. Пусть даны= смонотонно1 lim возрастающая= 2 lim( последовательность− ) = 2 − 1{x } иlimмонотонно( −убывающая) = 0 последовательность {y }. По теореме
Вейерштрасса , . . Т.к. , то с2-с1=0 , следовательно с1=с2=с(!).
→∞ →∞ →∞ n →∞ n
Утверждение 1: Последовательность сходится тогда и только тогда, когда сходится любая ее подпоследвательность.
13)Теорема Больцано-Вейерштрасса. Частичные пределы.
Определение.Частичным пределом последовательности называется предел какой-нибудь сходящейся подпоследовательности.
* Пример: Пусть 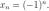 Эта последовательность расходится, но ее подпоследовательности
Эта последовательность расходится, но ее подпоследовательности  и
и  сходятся соответственно к 1 и -1.Таким
сходятся соответственно к 1 и -1.Таким
образом эти числа являются частичными пределами последовательности 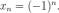
|
lim ( ) |
называется её верхним (нижним) пределом и |
|
Определение. Наибольший (наименьший) частичный предел числовой последовательности |
|||
обозначается символом |
− |
̅̅̅̅̅→∞ |
|
Теорема. Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
Доказательство (метод Больцано). Предположим, что 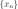 — ограниченна, тогда все члены последовательности принадлежат некоторому
— ограниченна, тогда все члены последовательности принадлежат некоторому
отрезку 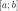 .
.
Разделим 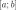 пополам. Мы получим два отрезка. Хотя бы один из них содержит бесконечное число членов последовательности. Выберем этот отрезок. Если оба обладают этим свойством, то выберем первый. Выбранный отрезок, который содержит бесконечное число членов данной
пополам. Мы получим два отрезка. Хотя бы один из них содержит бесконечное число членов последовательности. Выберем этот отрезок. Если оба обладают этим свойством, то выберем первый. Выбранный отрезок, который содержит бесконечное число членов данной
последовательности, обозначим 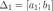 и его длина равна
и его длина равна 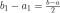 . Разделим отрезок
. Разделим отрезок 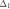 пополам, выберем из двух получившихся
пополам, выберем из двух получившихся
5

отрезков 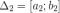 длина которого
длина которого 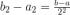 Продолжая эти рассуждения, мы получим последовательность отрезков
Продолжая эти рассуждения, мы получим последовательность отрезков 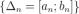 таких, что:
таких, что:
1.
2.
Следовательно, по определению, наша последовательность  стягивающаяся Тогда, по теореме Кантора, существует единственная точка С, принадлежащая всем отрезкам, то есть:
стягивающаяся Тогда, по теореме Кантора, существует единственная точка С, принадлежащая всем отрезкам, то есть:
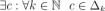 (1) .Покажем, что
(1) .Покажем, что 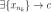 . Так как отрезок
. Так как отрезок 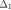 содержит бесконечное число членов последовательности
содержит бесконечное число членов последовательности 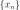 ,
,
то  . Отрезок
. Отрезок 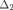 также содержит бесконечное число членов данной последовательности, и поэтому:
также содержит бесконечное число членов данной последовательности, и поэтому:  Вообще,
Вообще,  , где
, где  Следовательно, существует подпоследовательность
Следовательно, существует подпоследовательность  последовательности
последовательности 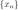 такая, что
такая, что 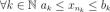 (2)
(2)
Условия (1) и (2) означают, что точка С и 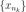 принадлежат отрезку
принадлежат отрезку  , и поэтому расстояние между ними не превосходит длины
, и поэтому расстояние между ними не превосходит длины
отрезка 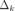 то есть: при
то есть: при  . По теореме о трех последовательностях
. По теореме о трех последовательностях 
Теорема доказана.
Замечание 1. Из любой ограниченной последовательности можно выделить монотонную подпоследовательность.
Замечание 2. Пусть {хn} — ограниченная последовательностъ, элементы которой находятся на сегменте [а, Ь]. Тогда предел с любой сходящейся подпоследовательности {xnk} также находится на сегменте [а, Ь].
14)Лемма об ограниченности последовательности Коши. Пример последовательности коши.
Определение. Последовательность {хn} называется фундаментальной, если для любого положительного ε найдется номер<N .такой, что для всех номеров n, удовлетворяющих условию n≥N, и для всех натуральных чисел р (р = 1,2,...) справедливо неравенство │xn+p-xn│
Теорема . Для того̅чтобы последовательность {хn} была сходящейся, необходимо и достаточно, чтобы она была ограниченной и чтобы ее верхний и
нижний пределы и совпадали.
номера. |
̅ |
̅ = |
|
̅ |
Доказательство. 1) Необходимость. Пусть последовательность {хn} сходится. Тогда она ограничена и имеет единственную предельную точку. Таким |
||||
образом, |
= . 2) Достаточность. Для любого ε > 0 интервал ( — ε, |
+ ε) содержит все элементы последовательности {хn}, начиная с некоторого |
||
Так как |
= |
, то указанный интервал совпадает с ε-окрестностью точки x, т. е. число x является пределом последовательности {xn}. |
||
Для любого положительного числа ε можно указать такой элемент xN фундаментальной последовательности, в ε-окрестности которого находятся все элементы последовательности, начиная с номера N. Иными словами, вне интервала (хм — ?, %n + s) находится не более чем конечное число элементов
последовательности.
Пример.
1) Покажем, что последовательность {1}- фундаментальная.
Доказательство. │1 − 1 │≤│ 1 │+│1│
Возьмем N=2+1,т.е.N>2. Тогда для любых ε больше 0 и для любых n>2 , выполняется │1 − 1 │≤│ 1 │+│1│≤2 <
2) Покажем, что последовательность 0,1,0,1,… не является фундаментальной.
Какой бы номер N мы не взяли, найдутся такие числа n, m=n+1, что │xn-xm│=│0-1│=1 ,т.е. последовательность не фундаментальна.
15)Критерий Коши сходимости последовательности. Примеры применения критерия.
Теорема (критерий Коши): Для того чтобы последовательность имела конечный предел, необходимо и достаточно, чтобы она была фундаментальной.
Доказательство. 1) Необходимость. Пусть последовательность {хn} сходится и х — ее предел. Требуется доказать, что эта последовательность является
фундаментальной. Возьмем любое положительное число ε. Из определения сходящейся последовательности вытекает, что для положительного числа ε/2 найдется номер N такой, что при n≥ N выполняется неравенство \хn — х\ < ε/2.
Если р — любое натуральное число, то при n≥N выполняется также и неравенство \хn+p— х\ < ε/2. Так как модуль суммы двух величин не больше суммы их модулей, то из последних двух неравенств получим, что при n≥N и для всех натуральных чисел р
Тем самым фундаментальность последовательности {хn} установлена.
2) Достаточность . Пусть {хn} — фундаментальная последовательность. Требуется доказать, что эта последовательность сходится. Согласно теореме достаточно для этого доказать ограниченность последовательности {хn} и равенство ее верхнего и нижнего пределов . Ограниченность
6

фундаментальной последовательности уже установлена нами выше. Для доказательства равенства верхнего и нижнего пределов воспользуемся
доказанным выше свойством фундаментальной последовательности: для любого положительного числа е можно указать элемент xN такой, что вне |
|||||||
̅ |
|
|
̅ |
|
|
|
|
интервала (xN— ε, xN+ ε) находится не более чем конечное число элементов последовательности. Интервал (xN— ε, xN+ ε) содержит интервал ( , |
|
), и |
|||||
поэтому – ≤ε |
, |
откуда, в силу произвольности ε, |
= |
. Тем самым сходимость последовательности установлена. Теорема полностью |
доказана. |
||
|
|
̅ |
|||||
Пример. Применим критерий Коши для установления сходимости следующей последовательности {xn}: xn=a1+a2+a3+…+an где ak (к = 1,2,3,...) — произвольные вещественные числа, удовлетворяющие условию \аk\ ≤ , a q — некоторое число из интервала 0 < q < 1. Пусть n— любой номер, р —
любое натуральное число. Тогда, очевидно,
Учитывая, что последовательность { } является бесконечно малой, можно утверждать, что для любого ε > 0 найдется номер N такой, что
 Стало быть, при n≥N и для любого натурального р
Стало быть, при n≥N и для любого натурального р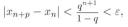 т. е. последовательность {xn} является фундаментальной и сходится согласно теореме.
т. е. последовательность {xn} является фундаментальной и сходится согласно теореме.
Пример: Докажем, что последовательность 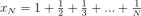 не является фундаментальной.
не является фундаментальной.
Покажем, что  расходящаяся :
расходящаяся :
Рассмотрим последовательность 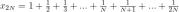 Доказательство проведем методом от противного. Предположим, что наша последовательность фундаментальная, тогда по определению фундаментальной последовательности:
Доказательство проведем методом от противного. Предположим, что наша последовательность фундаментальная, тогда по определению фундаментальной последовательности:
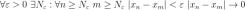 поскольку n и m любые, то возьмём
поскольку n и m любые, то возьмём 
таких слагаемых будет N штук, из всех слагаемых 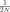 — наименьшее.
— наименьшее.
Можно сказать, что сумма будет больше, чем сумма N наименьших слагаемых, то есть:
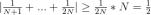 , а значит последовательность не является фундаментальной. Мы пришли к противоречию.
, а значит последовательность не является фундаментальной. Мы пришли к противоречию.
16)Бесконечно большие последовательности. Их свойства. Примеры.
Определение. Последовательность {хn} называется бесконечно большой, если для любого положительного числа A (сколь большим бы его не взяли) можно указать номер N такой, что при n≥N все элементы хn этой последовательности удовлетворяют неравенству \хn\ > А.
Замечание. Очевидно, что любая бесконечно большая последовательность является неограниченной, поскольку для лю- любого А > 0 можно указать номер N такой, что при n > N все элементы хn удовлетворяют неравенству \хn\ > А, а следовательно, для любого А > 0 найдется по крайней мере один такой элемент xn, что \хn\ > А.
Теорема (о связи б.м.п. и б.б.п.) Если {хn} — бесконечно большая последовательность, то, начиная с некоторого номера n, определена по- последовательность {1/xn}, которая является бесконечно малой. Если все элементы бесконечно малой последовательности {аn} не равны нулю, то
последовательность {1/аn} бесконечно большая.
Доказательство. Пусть {xn} – б.б.п, т.е. для любых > 0, существует Nε> 0, для любых n≥Nε, │xn│≥ε. Это означает, что n≥Nε все элементы xn≠ 0, поэтому последовательность {1/xn} имеет смысл начиная с некоторого номера Nε. Пусть А – любое положительное число, тогда для числа 1/А существует N1 такое что для любых n≥N1 │1/xn│<A, что по определению означает, что последовательность {1/xn} – бесконечно малая. Второе
доказательство проводится аналогично.
Свойства бесконечно больших последовательностей:
1)Сумма бесконечно больших последовательностей одного знака есть бесконечно большая последовательность того же знака.
Пусть  — бесконечно большие последовательности.
— бесконечно большие последовательности.
По определению:
Тогда для последовательности и . : > 0 = max{ 1,2} > 0 ≥ │ + │ ≥ , что означает, что
последовательность 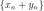 — бесконечно большая.
— бесконечно большая.
2)Сумма бесконечно большой и ограниченной последовательностей есть бесконечно большая последовательность.
Пусть последовательность — бесконечно большая, — ограниченная. Тогда по |
|
|
|||||
определению и . Рассмотрим : |
> 0 > 0 ≥ │ + │ ≥ |
|
|||||
│ + │ = │ │ |
│ │ |
= │ │ │ |
|
│ = │ │ │ |
+ |
, что |
|
|
│ + │ |
|
+ |
|
│=│xn│*(1+0)=│xn│≥ε Получили: |
|
|
означает, что последовательность 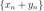 — бесконечно большая.
— бесконечно большая.
3)Произведение бесконечно больших последовательностей есть бесконечно большая последовательность. (Доказывается аналогично предыдущему)
7

4)Произведение бесконечно большой последовательности на константу есть бесконечно большая последовательность. Пусть последовательность 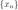 — бесконечно большая,
— бесконечно большая,  — константа. Тогда по определению
— константа. Тогда по определению 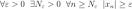 .
.
Рассмотрим 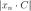 :
: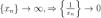
бесконечно большая. |
|
|
|
→ 0, тогда{ } → ∞ |
|
(по теореме о связи между бесконечно большими и бесконечно малыми последовательностями). |
|||||
— константа, |
— также константа, т.е. ограниченная. { 1 |
}={ |
1 1} |
|
, что означает, что последовательность — |
Примеры:
1.Последовательность  является бесконечно большой, т.к.
является бесконечно большой, т.к. 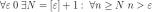 .
.
2.Последовательность 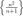 является бесконечно большой, т.к.
является бесконечно большой, т.к. 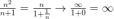 .
.
3.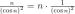 — бесконечно большая, т.к.
— бесконечно большая, т.к. 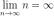 , а
, а 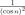 — ограниченная, сохраняющая знак.
— ограниченная, сохраняющая знак.
17)Понятие открытого, закрытого множеств, области на R, предельной точки множества. Примеры.
Определение> 01: Множество( )( − окрестностьЕ называется открытымточки ) ,=если( −все, его+точки) < являются внутренними, то есть если оно не содержит своих граничных точек.
̅( ) ̅ = ̅Определение− множество2: Множествовсех граничыхЕ называточектся. замкнутымзамыкание, еслиоперацияоно содеприсоединенияжит все свои предельныек мноеству(граничныеЕ множестваочкиего) точкиграничных. точек,. Если Е= , то
такое множество называется замкнутым.
Определение 1. Пусть X— непустое подмножество множества R. Точка a R называется предельной точкой множества X, если в любой окрестности Ua точки a найдётся, по крайней мере, одна, не совпадающая с a, точка множества X.
Лемма 1. Для того чтобы a R была предельной точкой непустого множества X R, необходимо и достаточно, чтобы в каждой окрестности этой точки содержалось бесконечное подмножество множества X.
Теорема 1. Для того чтобы точка a R была предельной точкой множества X R, необходимо и достаточно, чтобы существовала последовательность{xn} элементов множества X, отличных от a, сходящаяся к a.
Теорема . Всякое бесконечное множество действительных чисел имеет по крайней мере одну предельную точку.
̇ ε 2 ( , + проколотая окрестность точки а.
ε=(a- −,a)область на) . Область множества обладает свойствами:
1)Произвольная система замкнутых множеств в пересечении дает замкнутое множество;
2)Произвольная конечная система замкнутых множеств в объединении дает замкнутое множество.
Пример:
1)Если X = (0, 1), то любая точка a [0, 1] является предельной точкой множества множества X.
2) Если X = N, то предельной точкой множества X является только +∞.Как видно из примеров, предельная точка множества может как принадлежать,
так и не принадлежать ему.
*** Дополне́ние в теории множеств — это совокупность элементов, не принадлежащих данному множеству.
Определение: Множество Х является подмножеством Y, если любой элемент множества Х принадлежит множеству Y. Это еще называется нестрогим включением.
Способы задания множеств:
1.путем перечисления его элементов. Обычно перечислением задают конечные множества.
2.путем описания свойств, общих для всех элементов этого множества, и только этого множества. Это свойство называетсяхарактеристическим свойством, а такой способ задания множества описанием. Таким образом, можно задавать как конечные, так и бесконечные множества. Если мы задаем множество каким-либо свойством, потом может оказаться, что этим свойством обладает всего лишь один объект или вообще такого объекта
нет. Данный факт может быть совсем не очевиден.
18)Теорема о равносильности 2-ч определений предела функции. Замечания.
Определение 1. (определение по Коши или на языке ): |
|
|||
— предел функции |
в точке (и пишут |
|
, если: |
|
В определении допускается, что |
может не принадлежать области определения функции. |
|||
, то естьlim→ |
( ) = |
|
||
8

Определение 2. (определение по Гейне): называется пределом функции |
в точке , если |
, |
то есть |
, |
||
соответствующая последовательность значений |
, то есть |
. |
|
|
|
|
Эквивалентность определений |
|
|
|
|
|
|
Пусть число является пределом функции |
в точке по Коши. Выберем произвольную подходящую последовательность , |
, то есть |
||||
такую, для которой |
. Покажем, что является пределом по Гейне. |
|
|
|
|
|
Зададим произвольное  и укажем для него такое
и укажем для него такое  , что для всех
, что для всех  из условия
из условия  следует неравенство
следует неравенство  . В силу того,
. В силу того,
что |
, для найдётся такой номер , что будет выполняться неравенство |
, то есть |
. |
||||
качестве рассмотрим |
, а соответствующие |
0 > 0 > 0: 0 < │ − │ < → │ ( ) − │ ≥ |
|
|
|||
Докажем теперь обратное утверждение: предположим, что |
по Гейне, и покажем, что число является пределом функции в |
||||||
точке по Коши. Предположим, что это неверно, то есть: |
|
|
. В |
|
|||
|
|
|
значения будем обозначать . Тогда при любом выполняются |
|
|||
условия |
и |
. Отсюда следует, что последовательность является подходящей, но число не является пределом |
|||||
функции |
в точке . Получили противоречие. |
|
|
|
|
|
|
Замечание 1. |
Из определения предела функции по Гейне следует, что функция не может иметь в точке два разные предела. |
Замечание 2. |
Понятие предела функции в точке есть локальное понятие: существование и значение предела полностью определяется значениями |
функции в как угодно малой окрестности этой точки. |
|
Замечание 3. |
Данную запись в определении можно сформулировать иначе: точка принадлежит проколотой -окрестности |
точки ( |
). |
9
19. Критерий Коши существования предела функции.
Для того чтобы функция f, x 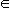 X, имела в (конечной или бесконечно удаленной) точке x0 конечный предел, необходимо и достаточно, чтобы
X, имела в (конечной или бесконечно удаленной) точке x0 конечный предел, необходимо и достаточно, чтобы
для любого  > 0существовала такая окрестность U(x0) точки x0, что для любых x'
> 0существовала такая окрестность U(x0) точки x0, что для любых x' 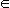 X
X  U(x0) и x"
U(x0) и x"  X
X  U(x0) выполнялось бы неравенство
U(x0) выполнялось бы неравенство
| f(x") - f(x')| <  .
.
Докажем необходимость условия.
Пусть 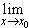 f(x) = a
f(x) = a 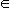 R, тогда для любого
R, тогда для любого  > 0 существует такая окрестность U(x0) точки x0, что для каждого x
> 0 существует такая окрестность U(x0) точки x0, что для каждого x  X
X  U(x0) справедливо неравенство
U(x0) справедливо неравенство
| f(x) -a| <  /2.
/2.
Поэтому если x'  X
X  U(x0) и x"
U(x0) и x"  X
X  U(x0), то
U(x0), то
|f(x") - f(x')| = |[f(x") - a] + [a - f(x')]| <
<|f(x") - a| + |a - f(x')| <  /2 +
/2 +  /2 =
/2 =  .
.
Докажем достаточность условий для существования конечного предела  f(x).
f(x).
Пусть произвольно фиксировано  > 0; тогда существует такая окрестность U(x0), что для всех x'
> 0; тогда существует такая окрестность U(x0), что для всех x'  X
X  U(x0) и всех
U(x0) и всех
x"  X
X  U(x0) выполняется неравенство | f(x") - f(x')| <
U(x0) выполняется неравенство | f(x") - f(x')| <  . Возьмем какую-либо последовательность xn
. Возьмем какую-либо последовательность xn x0, xn
x0, xn  X, n = 1, 2, ... В силу определения предела последовательности существует такой номер n0, что для всех
X, n = 1, 2, ... В силу определения предела последовательности существует такой номер n0, что для всех
n > n0 имеет место включение xn  U(x0), а поскольку xn
U(x0), а поскольку xn  X, то и включение xn
X, то и включение xn  X
X  U(x0). Тогда для всех номеров n > n0 и m > n0 будем иметь xn
U(x0). Тогда для всех номеров n > n0 и m > n0 будем иметь xn  X
X  U(x0), xm
U(x0), xm  X
X  U(x0), и, следовательно, будет выполняться неравенство | f(xn) - f(xm)| <
U(x0), и, следовательно, будет выполняться неравенство | f(xn) - f(xm)| <  . Это означает, что последовательность { f(xn)} удовлетворяет критерию сходимости Коши
. Это означает, что последовательность { f(xn)} удовлетворяет критерию сходимости Коши
для последовательностей и, следовательно, имеет конечный предел.
20. 4 теоремы о функциях, имеющих предел.
Теорема 4.2. Если функция в данной точке 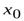 имеет предел, то она ограничена в некоторой окрестности точки
имеет предел, то она ограничена в некоторой окрестности точки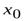 , то есть
, то есть
 ,
, 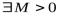 ,
,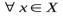 :
: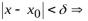
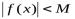 .
.
Доказательство. Обозначим 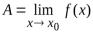 и рассмотрим
и рассмотрим . Из определения
. Из определения
4.3. следует существование такого  , что для всякого
, что для всякого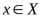 из неравенств
из неравенств
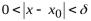 вытекает неравенство
вытекает неравенство 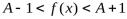 . Остается положить
. Остается положить
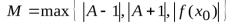 .Теорема доказана.
.Теорема доказана.
Использование определения предела функции по Гейне позволяет перенести утверждения, доказанные ранее для последовательностей, на случай произвольных функций.
Теорема 4.3. Пусть функции 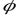 ,
,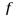 и
и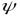 определены на множестве
определены на множестве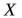 , на котором
, на котором
выполняются неравенства 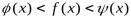 . Пусть существуют
. Пусть существуют 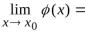
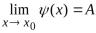 , тогда
, тогда 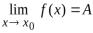 .
.
Доказательство непосредственно вытекает из определения предела функции по Гейне и леммы о двух милиционерах.
Теорема 4.4. Пусть функции 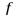 и
и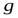 определены на множестве
определены на множестве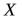 . Пусть
. Пусть
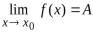 и
и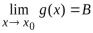 . Тогда
. Тогда
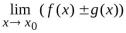 =
= ;
;
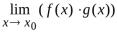 =
= ;
;
и, если при любом 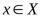
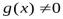 и
и 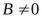 , то
, то
 =
= .
.
Доказательство. Ограничимся рассмотрением случая отношения двух функций. Выберем произвольно последовательность 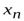 ,
,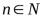 , для которой
, для которой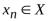 ,
,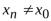 при любом
при любом и
и 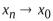 . Тогда
. Тогда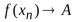 ,
,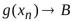 и по теореме 3.12.
и по теореме 3.12.
.
21.Теоремы о бесконечно малых функциях.
Если 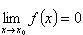 , то функция f называется бесконечно малой при x → x0
, то функция f называется бесконечно малой при x → x0

Теорема 1. Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
Пусть α(х) и ß(х) — две б.м. функции при х→хо. Это значит, что lim α(х)=0, при х→х0 т.е. для любого ε>0, а значит, и ε/2>0 найдется число δ1>0 такое, что для всех х, удовлетворяющих неравенству 0<|х-х0|<δ1, выполняется неравенство
Пусть δ — наименьшее из чисел δ1 и δ2.Тогда для всех х, удовлетворяющих неравенству 0<|х-хо|<δ, выполняются оба неравенства. Следовательно, имеет место
соотношение
Таким образом
Аналогично проводится доказательство для любого конечного числа б.м. функций.
Теорема 2. Произведение ограниченной функции на бесконечно малую функцию
есть функция бесконечно малая.
Пусть функция ƒ(х) ограничена при х→х0. Тогда существует такое число М>0, что
для всех х из δ1-окрестности точки хо. И пусть α(х)—б.м.ф. при х→x0. Тогда для любого ε >0, а значит, и ε /М> 0 найдется такое число δ2>О, что при всех х, удовлетворяющих неравенству 0<|х-хо|<δ2, выполняется неравенство
Обозначим через δ наименьшее из чисел δ1 и δ2. Тогда для всех х, удовлетворяющих неравенству 0<|х-хо|<δ, выполняются оба неравенства.
Следовательно, |ƒ(х)-α(х)|=|ƒ(х)|-|а(х)|<ε.
А это означает, что произведение ƒ(х)•α(х) при х→х0 есть бесконечно малая
функция.
Следствие 1. Так как всякая б.м.ф. ограничена, то из теоремы 2 вытекает: произведение двух б.м.ф. есть функция бесконечно малая.
Следствие 2. Произведение б.м.ф. на число есть функция бесконечно малая.

Теорема 3. Частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая.
17.2(Теорема 2)
Теорема 5. Если функция ƒ(х) имеем предел, равный А, то ее можно представить как сумму числа А и бесконечно малой функции α(х), т. е. если limƒ(х)=А, при Х→Хо то ƒ(х)=А+а(х).
Пусть  Следовательно,
Следовательно,
т. е. |ƒ(х)-А-0|<ε. Это означает, что функция ƒ(х)-А имеет предел, равный нулю, т. е. является б.м.ф., которую обозначим через α(х): ƒ(х)-А=α(х). Отсюда ƒ(х)=А+α(х).
Теорема 6(обратная). Если функцию ƒ(х) можно представить в виде суммы числа А и бесконечно малой функции α(х), то число А является пределом функции ƒ(х), т. е. если ƒ(х)=А+α(х), то lim ƒ(х)=А при Х→Хо
22. Теоремы о непрерывности арифметических операций.
Теорема. Если две функции f (x) и g (x) определены в одном и том же
промежутке Р и обе непрерывны в точке х0, то в этой же точке будут непрерывны и функции f (x) ± g (x), f (x)·g (x), 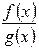 , последняя при условии, что g(x) не равна 0.
, последняя при условии, что g(x) не равна 0.

Это непосредственно вытекает из теорем о пределе суммы (разности), произведения и частного двух функций, имеющих порознь пределы.
Остановимся для примера на частном двух функций. Предположение о непрерывности функций f (x) и g (x) в точке х0 равносильно наличию равенств
.
Но отсюда, по теореме о пределе частного (так как предел знаменателя не нуль), имеем:
,
а это равенство и означает, что функция 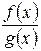 непрерывна в точке х0.
непрерывна в точке х0.
Следствия.
1.Линейная комбинация непрерывных функций есть функция непрерывная.
2.Произведение конечного числа непрерывных функций есть функция непрерывная.
3.Если f (x) непрерывна, то непрерывна и |f (x)|.
23. Свойства бесконечно больших функций. Примеры.
функция f(x), определенная в окрестности точки х0, наз. бесконечно большой функцией при х, стремящемся к x0, если для любого числа М > 0 найдется такое число δ = δ (М) > 0, что для всех х ≠ х0 и таких, что |х - х0 | < δ, выполняется

неравенство |f(x)| > M. |
|
|
|
||
|
|
|
|
||
|
Пример. Функция |
есть бесконечно большая функция при |
. |
||
|
Если |
стремится к бесконечности при |
и принимает лишь |
|
|
|
положительные значения, то пишут |
; если лишь |
|
||
|
отрицательные значения, то |
. |
|
||
|
|
|
|
|
|
|
Функция двух переменных |
|
в окрестности точки |
|
|
|
(начало координат) является бесконечно большой функцией, так |
|
|||
|
как |
|
. |
|
|
|
|
|
|
|
|
24. Теорема об односторонних пределах.
Под односторонним пределом числовой функции подразумевают «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторонним пределом (или пределом слева)
и правосторонним пределом (пределом справа).
Число 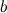 называется правым пределом функции
называется правым пределом функции 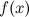 в точке
в точке  , если для
, если для 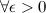
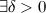 такое, что для любого
такое, что для любого 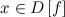 и
и  , выполняется неравенство
, выполняется неравенство 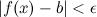
(рис. 1). Правый предел обозначается 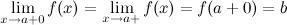
Число 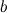 называется левым пределом функции
называется левым пределом функции 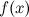 в точке
в точке  , если для
, если для 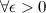
 такое, что для любого
такое, что для любого 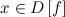 и
и 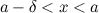 , выполняется неравенство
, выполняется неравенство 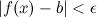
(рис. 2). Левый предел обозначается 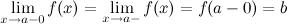

Теорема. Функция  имеет предел в точке
имеет предел в точке  тогда и только тогда, когда существуют равные между собой односторонние пределы в этой точке. В этом случае их общее значение является пределом функции в точке
тогда и только тогда, когда существуют равные между собой односторонние пределы в этой точке. В этом случае их общее значение является пределом функции в точке 
Доказательство
Необходимость.
Пусть в точке  существует конечный предел, то
существует конечный предел, то
есть |
|
из чего следует, что этот же предел |
существует на промежутках |
. Следовательно |
|
односторонние пределы существуют и равны между собой. |
||
Достаточность. |
|
|
Пусть в точке |
существуют односторонние пределы, равные между |
|
собой |
и |
из чего следует, |
что теорема доказана.
Пример.
Дана функция
Выяснить существует ли предел в точке 
Рассмотрим поведение функции в окрестности точки  . Как видно
. Как видно 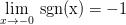
и |
Пределы справа и слева не равны. Согласно вышеприведенной |
теореме, можно сделать вывод, что предел функции в точке 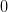 не существует.
не существует.
25. Теорема о втором замечательном пределе.
Доказательство.
Доказательство второго замечательного предела для случая последовательности (т.е. для Натуральных значений x)
Докажем вначале теорему для случая последовательности 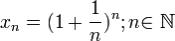 По формуле бинома Ньютона:
По формуле бинома Ньютона:
Полагая |
, получим: |

(1)
Из данного равенства (1) следует, что с увеличением n число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении n число 
убывет, поэтому величины 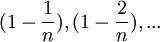
возрастают. Поэтому последовательность 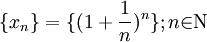 — возрастающая, при этом
— возрастающая, при этом
(2).
Покажем, что она ограничена. Заменим каждую скобку в правой части равенства на единицу, правая часть увеличится, получим неравенство
Усилим полученное неравенство, заменим 3,4,5,…, стоящие в знаменателях дробей, числом 2:
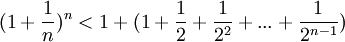 .
.
Сумму в скобке найдем по формуле суммы членов геометрической прогрессии:
|
. |
Поэтому |
(3). |
Итак, последовательность ограничена сверху, при этом |
|
выполняются неравенства (2) и (3): |
. |
Следовательно, на основании теоремы Вейерштрасса (критерий сходимости последовательно
сти) последовательность 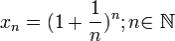
монотонно возрастает и ограниченна, значит имеет предел, обозначаемый буквой e. Т.е.
Зная, что второй замечательный предел верен для натуральных значений x, докажем второй
замечательный предел для вещественных x, т.е. докажем, что 
Рассмотрим два случая: 1. Пусть 
каждое значение x заключено между двумя положительными целыми числами: 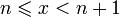 , где n = [x] - это целая часть x.
, где n = [x] - это целая часть x.
Отсюда следует: 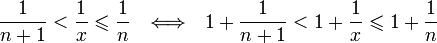 , поэтому
, поэтому
.

Если  , то
, то 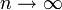 . Поэтому, согласно пределу
. Поэтому, согласно пределу  , имеем:
, имеем:
.
По признаку (о пределе промежуточной функции) существования пределов
.
2. Пусть 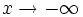 . Сделаем подстановку − x = t, тогда
. Сделаем подстановку − x = t, тогда
.
Из двух этих случаев вытекает, что 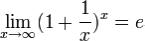 для любого x.
для любого x.
26. Теорема о замене переменной в пределах. Следствие из теоремы о втором замечательном пределе.
Если существуют
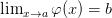 и
и 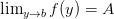
причем для всех х из некоторой проколотой окрестности точки  выполняется
выполняется
условие 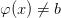 , то в точке
, то в точке  существует предел сложной функции
существует предел сложной функции 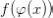 и справедливо равенство
и справедливо равенство
Проводим доказательство, используя определение предела функции по Гейне
Следствия:

Доказательство следствия
27. Следствия 2-4 из теоремы о втором замечательном пределе.
Замечательный логарифмический предел
Доказательство предела
Замечательный показательный предел
Следствия
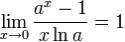 для
для 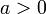 ,
, 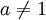
Доказательство предела
Доказательство следствия
Замечательный степенной предел
Доказательство предела
28. Теорема о первом замечательном пределе.
Доказательство

Рассмотрим односторонние пределы 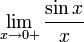 и
и 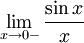 и докажем, что они равны 1.
и докажем, что они равны 1.
Пусть 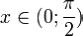 . Отложим этот угол на единичной окружности (R = 1). Точка K — точка пересечения луча с окружностью, а точка L —
. Отложим этот угол на единичной окружности (R = 1). Точка K — точка пересечения луча с окружностью, а точка L —
с касательной к единичной окружности в точке(1;0). Точка H — проекция точки K на ось OX.
Очевидно, что:
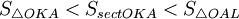 (1)
(1)
(где SsectOKA — площадь сектора OKA)
(из  : | LA | = tgx)
: | LA | = tgx)
Подставляя в (1), получим:
Так как при 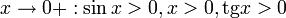 :
:
Умножаем на sinx:
Перейдём к пределу:
