20 Виды нагружения стержня
№1 Любая комбинация простых деформаций стержня называется …
|
|
|
деформированным состоянием |
|
|
|
напряженным состоянием |
|
|
|
сложным сопротивлением |
|
|
|
тензором деформации |
№2
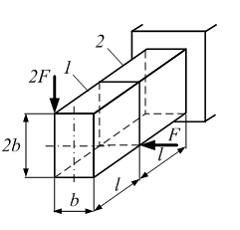На
стержень действуют внешние силы F
и 2F.
Сечение прямоугольное с размерами b
и 2b.
Участки стержня испытывают:
а) 1 –
кручение, 2 – косой изгиб;
б) 1 – плоский
поперечный изгиб, 2 – кручение и плоский
поперечный изгиб;
в) 1 – кручение и
плоский поперечный изгиб, 2 – косой
изгиб;
г) 1 – кручение и плоский
поперечный изгиб, 2 – кручение и косой
изгиб.
|
|
|
а |
|
|
|
в |
|
|
|
б |
|
|
|
г |
№3 Оценку прочности материала при заданном напряженном состоянии в опасной точке стержня с круглым сечением проводят с использованием теорий прочности при: а) внецентренном растяжении; б) растяжении и плоском изгибе; в) плоском поперечном изгибе; г) кручении и изгибе.
|
|
|
в |
|
|
|
а |
|
|
|
г |
|
|
|
б |
№4
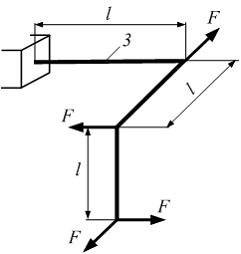Схема
нагружения стержня внешними силами
представлена на рисунке. Длины участков
одинаковы и равны l.
Третий участок стержня испытывает
деформации …
|
|
|
кручение и растяжение |
|
|
|
растяжение, кручение и чистый изгиб |
|
|
|
кручение и плоский поперечный изгиб |
|
|
|
кручение и чистый изгиб |
№5 Напряженное состояние в опасных точках круглого поперечного сечения стержня считается плоским для случая: а) плоский изгиб; б) растяжение и плоский изгиб; в) внецентренное растяжение; г) растяжение с кручением.
|
|
|
г |
|
|
|
а |
|
|
|
в |
|
|
|
б |
№6 Напряженное состояние в опасных точках круглого поперечного сечения стержня считается линейным для случая: а) изгиб с кручением; б) растяжение с кручением; в) внецентренное растяжение; г) кручение и внецентренное сжатие.
|
|
|
в |
|
|
|
а |
|
|
|
б |
|
|
|
г |
№7
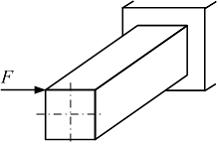При
данном варианте нагружения стержень
прямоугольного поперечного сечения
испытывает …
|
|
|
косой изгиб |
|
|
|
кручение и чистый изгиб |
|
|
|
плоский поперечный изгиб |
|
|
|
кручение и плоский поперечный изгиб |
№8
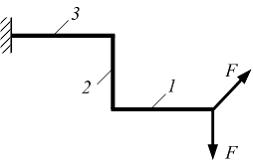Схема
нагружения стержня квадратного сечения
внешними силами показана на рисунке
(одна сила лежит в плоскости чертежа,
вторая – перпендикулярно плоскости).
Деформации (растяжение, кручение и
плоский поперечный изгиб) одновременно
возникают на участке (-ах) …
|
|
|
2, 3 |
|
|
|
1 |
|
|
|
3 |
|
|
|
2 |
№9 При выводе формул для определения напряжений в точке поперечного сечения стрежня при сложном сопротивлении используется …
|
|
|
принцип неизменности начальных размеров |
|
|
|
гипотеза об изотропности материала |
|
|
|
принцип независимости действия сил |
|
|
|
гипотеза о сплошности материала |