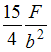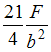- •Растяжение и сжатие
- •О сновные механические характеристики материалов
- •Линейное напряженное состояние
- •Напряженное и деформированное состояние
- •Плоское напряженное состояние
- •О бъемное напряженное состояние
- •Потенциальная энергия деформации
- •Теории прочности
- •Чистый сдвиг
- •Геометрические характеристики плоских сечений
- •Просуммировав (проинтегрировав) такие произведения по всей площади фигуры, получаем статические моменты относительно осей y и X: ; [см3, м3, т.Д.].
- •М оменты инерции сечения
- •Моменты сопротивления.
- •Кручение
- •Кручение бруса прямоугольного сечения
- •Определение перемещений в балках при изгибе
- •Сложное сопротивление
- •Изгиб с растяжением (внецентренное сжатие–растяжение).
- •Изгиб с кручением
- •Общие методы определения перемещений
- •Статически неопределимые системы
- •Расчет плоских кривых брусьев (стержней)
- •Устойчивость сжатых стержней. Продольный изгиб
- •"Два" слова о шпорах по сопротивлению материалов
- •1 Внутренние силы и напряжения
- •5 Продольная сила. Напряжения и деформации
- •6 Механические свойства и механические характеристики материалов
- •7 Расчеты стержней на прочность и жесткость
- •8 Испытание конструкционных материалов на растяжение и сжатие
- •9 Расчет на прочность при кручении
- •10 Расчет на жесткость при кручении
- •11 Чистый сдвиг. Расчет на сдвиг (срез)
- •12 Крутящий момент. Деформации и напряжения
- •13 Перемещения при изгибе. Расчет балок на жесткость
- •14 Напряжения в поперечном сечении стержня при плоском изгибе
- •15 Поперечная сила, изгибающий момент и их эпюры
- •16 Расчет балок на прочность
- •17 Изгиб с растяжением? Сжатием
- •18 Пространственный и косой изгиб
- •19 Изгиб с кручением
- •20 Виды нагружения стержня
14 Напряжения в поперечном сечении стержня при плоском изгибе
№1
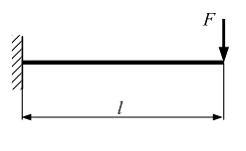
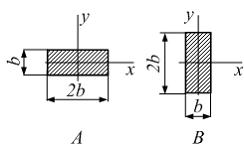 Консольная
балка длиной l
имеет два варианта расположения
прямоугольного поперечного сечения.
Сила F,
линейные размеры b
и h
заданы. В опасном сечении балки отношение
наибольших нормальных напряжений
Консольная
балка длиной l
имеет два варианта расположения
прямоугольного поперечного сечения.
Сила F,
линейные размеры b
и h
заданы. В опасном сечении балки отношение
наибольших нормальных напряжений
![]() равно …
равно …
|
|
|
6 |
|
|
|
1 |
|
|
|
2 |
|
|
|
4 |
№2
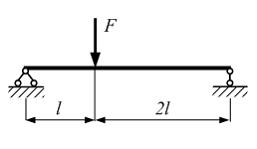
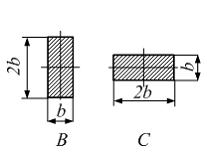 Прямоугольная
балка имеет два варианта расположения
прямоугольного поперечного сечения.
Сила − F,
линейные размеры b
и l
заданы. Отношение наибольших касательных
напряжений
Прямоугольная
балка имеет два варианта расположения
прямоугольного поперечного сечения.
Сила − F,
линейные размеры b
и l
заданы. Отношение наибольших касательных
напряжений
![]() ,
возникающих в балке, равно …
,
возникающих в балке, равно …
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
3 |
№3
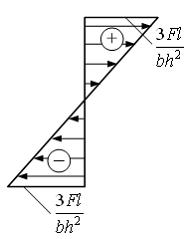
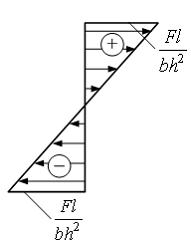
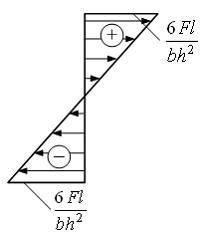
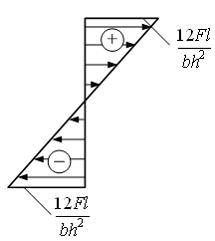
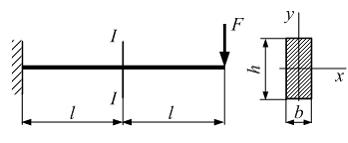 Эпюра
распределения нормальных напряжений
по высоте сечения балки I–I с размерами
b и h
имеет вид …
Эпюра
распределения нормальных напряжений
по высоте сечения балки I–I с размерами
b и h
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№4
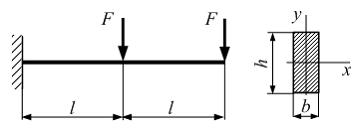 Консольная
балка прямоугольного сечения с размерами
b
и h
нагружена силами F.
Линейный размер
Консольная
балка прямоугольного сечения с размерами
b
и h
нагружена силами F.
Линейный размер
![]() .
Отношение максимального нормального
напряжения к максимальному касательному
напряжению в балке
.
Отношение максимального нормального
напряжения к максимальному касательному
напряжению в балке
![]() равно …
равно …
|
|
|
10 |
|
|
|
40 |
|
|
|
80 |
|
|
|
60 |
№5
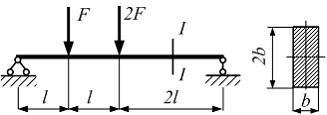 Балка
прямоугольного поперечного сечения
нагружена внешними силами, как показано
на рисунке. Значение максимального
касательного напряжения в сечении
Балка
прямоугольного поперечного сечения
нагружена внешними силами, как показано
на рисунке. Значение максимального
касательного напряжения в сечении
![]() равно …
равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№6
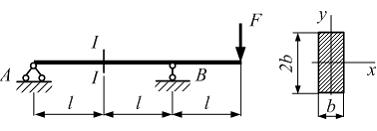 Однопролетная
консольная балка прямоугольного сечения
с размерами b
и 2b
нагружена силой F.
Линейные размеры b
и
l = 20b
заданы. В
сечении I–I значение максимального
касательного напряжения равно τ.
Максимальное нормальное напряжение в
балке равно …
Однопролетная
консольная балка прямоугольного сечения
с размерами b
и 2b
нагружена силой F.
Линейные размеры b
и
l = 20b
заданы. В
сечении I–I значение максимального
касательного напряжения равно τ.
Максимальное нормальное напряжение в
балке равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№7
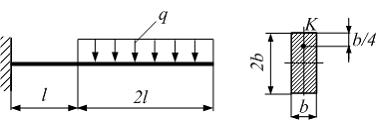 Интенсивность
равномерно распределенной нагрузки
− q,
линейные размеры b
и l
заданы. Значение нормального напряжения
в точке К
опасного
сечения балки равно …
Интенсивность
равномерно распределенной нагрузки
− q,
линейные размеры b
и l
заданы. Значение нормального напряжения
в точке К
опасного
сечения балки равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№8
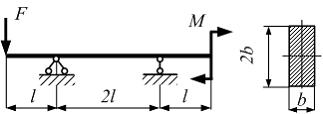 Балка
нагружена силой
Балка
нагружена силой
![]() и
моментом
и
моментом
![]() .
Размер
.
Размер
![]() ;
;
![]() .
Значение максимального нормального
напряжения в балке равно___________ МПа.
.
Значение максимального нормального
напряжения в балке равно___________ МПа.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№9
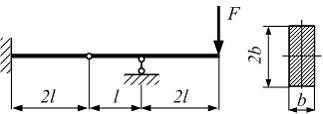 Схема
нагружения балки прямоугольного сечения
показана на рисунке. Сила − F,
линейные размеры b
и l
заданы. Значение максимального нормального
напряжения в балке равно …
Схема
нагружения балки прямоугольного сечения
показана на рисунке. Сила − F,
линейные размеры b
и l
заданы. Значение максимального нормального
напряжения в балке равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|