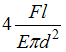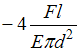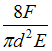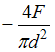- •Растяжение и сжатие
- •О сновные механические характеристики материалов
- •Линейное напряженное состояние
- •Напряженное и деформированное состояние
- •Плоское напряженное состояние
- •О бъемное напряженное состояние
- •Потенциальная энергия деформации
- •Теории прочности
- •Чистый сдвиг
- •Геометрические характеристики плоских сечений
- •Просуммировав (проинтегрировав) такие произведения по всей площади фигуры, получаем статические моменты относительно осей y и X: ; [см3, м3, т.Д.].
- •М оменты инерции сечения
- •Моменты сопротивления.
- •Кручение
- •Кручение бруса прямоугольного сечения
- •Определение перемещений в балках при изгибе
- •Сложное сопротивление
- •Изгиб с растяжением (внецентренное сжатие–растяжение).
- •Изгиб с кручением
- •Общие методы определения перемещений
- •Статически неопределимые системы
- •Расчет плоских кривых брусьев (стержней)
- •Устойчивость сжатых стержней. Продольный изгиб
- •"Два" слова о шпорах по сопротивлению материалов
- •1 Внутренние силы и напряжения
- •5 Продольная сила. Напряжения и деформации
- •6 Механические свойства и механические характеристики материалов
- •7 Расчеты стержней на прочность и жесткость
- •8 Испытание конструкционных материалов на растяжение и сжатие
- •9 Расчет на прочность при кручении
- •10 Расчет на жесткость при кручении
- •11 Чистый сдвиг. Расчет на сдвиг (срез)
- •12 Крутящий момент. Деформации и напряжения
- •13 Перемещения при изгибе. Расчет балок на жесткость
- •14 Напряжения в поперечном сечении стержня при плоском изгибе
- •15 Поперечная сила, изгибающий момент и их эпюры
- •16 Расчет балок на прочность
- •17 Изгиб с растяжением? Сжатием
- •18 Пространственный и косой изгиб
- •19 Изгиб с кручением
- •20 Виды нагружения стержня
5 Продольная сила. Напряжения и деформации
№1
 Стержень
изготовлен из изотропного материала
(см. рисунок) и работает в линейно-упругой
области. Связь между продольной
деформацией и нормальными напряжениями
в поперечном сечении имеет вид …
Стержень
изготовлен из изотропного материала
(см. рисунок) и работает в линейно-упругой
области. Связь между продольной
деформацией и нормальными напряжениями
в поперечном сечении имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№2
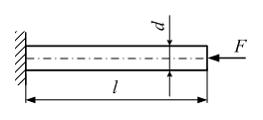 Для
стержня круглого поперечного сечения
диаметром d,
схема которого изображена на рисунке,
абсолютное укорочение
Для
стержня круглого поперечного сечения
диаметром d,
схема которого изображена на рисунке,
абсолютное укорочение
![]() равно _______ .
Модуль упругости материала Е
задан.
равно _______ .
Модуль упругости материала Е
задан.
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
№3 Продольная сила есть равнодействующая …
|
|
|
всех внешних сил, приложенных к стержню |
|
|
|
внешних сил, приложенных к отсеченной части стержня |
|
|
|
нормальных напряжений и внешних сил, приложенных к отсеченной части стержня |
|
|
|
нормальных напряжений в поперечном сечении стержня |
№4 Вдали от мест нагружения характер распределения нормальных напряжений по площади поперечного сечения при растяжении − сжатии зависит от …
|
|
|
способа приложения внешних сил |
|
|
|
статического эквивалента внешней нагрузки |
|
|
|
величины и способа приложения внешних сил |
|
|
|
формы поперечного сечения |
№5
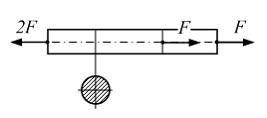 На
рисунке показан стержень, растянутый
силами, направленными вдоль оси стержня.
Равномерное распределение линейных
продольных деформаций в поперечном
сечении, достаточно удаленных от мест
приложения сил, является следствием …
На
рисунке показан стержень, растянутый
силами, направленными вдоль оси стержня.
Равномерное распределение линейных
продольных деформаций в поперечном
сечении, достаточно удаленных от мест
приложения сил, является следствием …
|
|
|
гипотезы сплошной среды |
|
|
|
гипотезы плоских сечений |
|
|
|
принципа суперпозиции |
|
|
|
гипотезы однородности материала |
№6
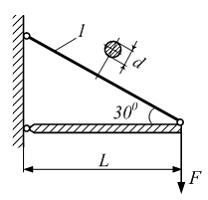 Абсолютно
жесткий элемент (заштрихованный)
поддерживается упругим стержнем 1. Сила
Абсолютно
жесткий элемент (заштрихованный)
поддерживается упругим стержнем 1. Сила
![]() длина
длина
![]() диаметр
диаметр
![]() и
модуль упругости материала стержня Е
известны. Линейная продольная деформация
стержня 1 равна …
и
модуль упругости материала стержня Е
известны. Линейная продольная деформация
стержня 1 равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№7
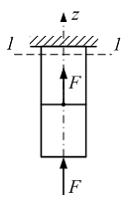 Стержень
круглого поперечного сечения диаметром
d нагружен
так, как показано на рисунке. Нормальные
напряжения в сечении 1−1 равны …
Стержень
круглого поперечного сечения диаметром
d нагружен
так, как показано на рисунке. Нормальные
напряжения в сечении 1−1 равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№8
 Для
стержня, схема которого изображена на
рисунке, продольная сила N
в сечении 2−2 …
Для
стержня, схема которого изображена на
рисунке, продольная сила N
в сечении 2−2 …
|
|
|
сжимающая
и равна
|
|
|
|
растягивающая и равна F |
|
|
|
равна нулю |
|
|
|
сжимающая
и равна
|
№9
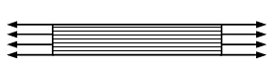 На
рисунке показан растянутый стержень.
Между продольными слоями материала …
На
рисунке показан растянутый стержень.
Между продольными слоями материала …
|
|
|
действуют касательные напряжения |
|
|
|
действуют нормальные напряжения |
|
|
|
отсутствуют нормальные и касательные напряжения |
|
|
|
действуют нормальные и касательные напряжения |
№10
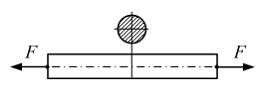 На
рисунке показан стержень, растянутый
силами
На
рисунке показан стержень, растянутый
силами
![]() .
Равномерный характер распределения
нормальных напряжений по площади
поперечных сечений (расположенных вдали
от точек приложения сил) является
следствием …
.
Равномерный характер распределения
нормальных напряжений по площади
поперечных сечений (расположенных вдали
от точек приложения сил) является
следствием …
|
|
|
гипотезы плоских сечений (гипотезы Бернулли) |
|
|
|
гипотезы однородности материла |
|
|
|
принципа суперпозиции |
|
|
|
гипотезы сплошной среды |