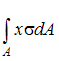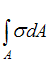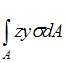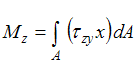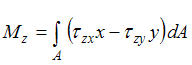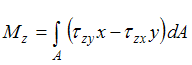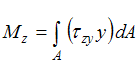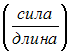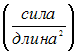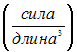"Два" слова о шпорах по сопротивлению материалов

• К сожалению, в сопромате нет единообразия не только в обозначениях, но и в выборе осей координат, и в представлении некоторых формул, и в некоторых построениях. Например, прогиб балки могут обозначать и "w", и "y", и "z" и ..., а положительным одни считают прогиб направленный вниз, другие - вверх. И таких приятностей масса. Таким образом, универсальной шпоры по сопротивлению материалов создать невозможно, всегда надо учитывать специфику своего ВУЗа. Но общее, конечно, есть у всех.

• Вам предлагаются и привычные шпоры на ма-а-а-леньких листочках, которые называются "Весь сопромат на 2-х страницах", и целый Труд на десятках!!! страницах. По нему, кстати, удобно делать такую странную вещь, как готовиться к экзамену. Если сравнить с "кирпичами", которые в библиотеке, или с конспектом коллеги, написанным корявым почерком, то выигрыш налицо.

• Для порядка перечислим "кирпичи", на базе которых создавались шпоры:

  • Беляев Н.М. Сопротивление материалов.

  • Гастев В.А. Краткий курс сопротивления материалов.

  • Дарков А.В., Шпиро Г.С. Сопротивление материалов.

  • Писаренко Г.С. Сопротивление материалов.

  • Писаренко Г.С., Яковлев А.П., Матвеев В.В. Справочник по сопротивлению материалов.

  • Федосьев В.И. Сопротивление материалов.

На экзамене весьма полезно упомянуть кого-нибудь из них, только не переборщите.

• Шпоры подразделены на отдельные разделы и снабжены алфавитным указателем, который позволяет быстро найти ответ на поставленный черте кем черте какой вопрос.

• Шпаргалки подготовлены в Word. Можете загружать, копировать и улучшать.

• Возможно, Вам читается не все, поэтому какие-то куски можно опустить. Но многолетний опыт общения со студентами разных вузов определил некий стандарт курса сопромата.

• Для особо экономных сделаны "выжимки" - только формулы, что довольно бессмысленно, но почему-то популярно.

• Ни пуха, ни пера!

1 Внутренние силы и напряжения

№1 Нормальное напряжение в точке сечения − это …

			проекция вектора касательного напряжения в точке на нормаль к сечению
			проекция вектора полного напряжения в точке на плоскость сечения
			геометрическая сумма векторов полного и касательного напряжений в точке
			проекция вектора полного напряжения в точке на нормаль к сечению

№2 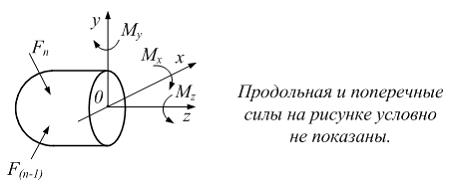Интегральная связь между изгибающим моментом  и нормальными напряжениями имеет вид 

№3 Если известно нормальное и касательное напряжения в точке сечения, то полное напряжение в этой точке определяется по формуле 

№4 Внутренними силовыми факторами называются …

			проекции внешних сил отсеченной части на главные центральные оси сечения
			главный вектор и главный момент всех внутренних сил в сечении
			момент внешних сил отсеченной части относительно главных центральных осей сечения
			проекции главного вектора и главного момента внутренних сил на координатные оси x, y, z, одна из которых перпендикулярна к плоскости сечения, а две другие лежат в этой плоскости (начало координат располагается в центре тяжести сечения)

№5 Для определения внутренних силовых факторов, действующих в сечении тела, используется …

			метод сил
			метод сечений
			принцип независимости действия сил
			гипотеза плоских сечений

№6

Касательным напряжением в точке сечения называется …

			проекция вектора нормального напряжения в точке на направление вектора полного напряжения в данной точке
			проекция вектора полного напряжения в точке на нормаль к сечению
			геометрическая сумма векторов полного и нормального напряжений в точке
			ортогональная проекция вектора полного напряжения на плоскость сечения

№7 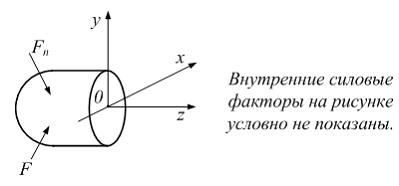Крутящий момент  ( ) и изгибающие моменты  и  лежат в плоскостях …

№8

Интегральная связь между крутящим моментом  ( ) и касательными напряжениями имеет вид …

2 Перемещения и деформации №1 Вектор полного линейного перемещения точки в общем случае …

			нельзя разложить на три составляющих вектора, направленных вдоль координатных осей
			можно продолжить в направлении вектора
			можно разложить на три составляющих вектора, направленных вдоль координатных осей
			можно разложить только на два составляющих вектора, направленных вдоль координатных осей

№2 Вектором полного перемещения точки деформируемого тела называется вектор, …

			имеющий начало в точке недеформированного тела, а конец в той же точке деформированного тела
			соединяющий две точки деформированного тела
			соединяющий две точки недеформированного тела
			имеющий начало в точке недеформированного тела, а конец в той же точке тела находящегося в процессе деформирования

№3

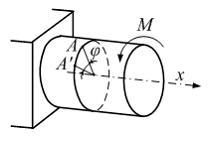Величина φ является …

			углом поворота стержня
			углом поворота точки А
			угловым перемещением центра тяжести поперечного сечения
			угловым перемещением поперечного сечения стержня

№4 Размерность линейной деформации – …

№5 Если известны углы поворота малого прямолинейного отрезка в трех координатных плоскостях  то полный угол поворота определяется по формуле

№6 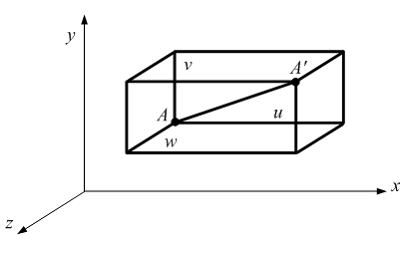Если известны перемещения точки A (см. рисунок) вдоль координатных осей (u, v, w), то полное перемещение определяется по формуле …

№7 Линейная деформация − это …

			среднее перемещение в точке
			полное перемещение точки
			количественная мера изменения линейных размеров в точке

№8 Угловая деформация − это …

			угол поворота прямого отрезка малой длины в пространстве
			изменение угла между двумя взаимно перпендикулярными до деформации малыми отрезками, проходящими через данную точку.
			сумма углов поворота прямого отрезка малой длины в координатных плоскостях
			угол поворота тела в пространстве как жесткого целого

№9 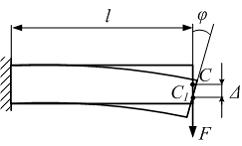Величина  является …

			угловым перемещением поперечного сечения при плоском изгибе
			линейным перемещением поперечного сечения при плоском изгибе
			углом поворота стержня
			углом поворота поперечного сечения вокруг оси стержня

№10 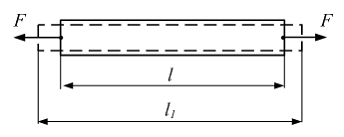Первоначальная длина стержня (см. рисунок) равна l. После приложения растягивающих сил длина стержня стала l₁. Величина  называется …

			напряжением
			относительным удлинением
			абсолютным укорочением
			абсолютным удлинением

3 Основные понятия, определения, допущения и принципы №1 Свойство материала тела восстанавливать свою первоначальную форму и размеры после снятия нагрузки называется …

			однородностью
			твердостью
			упругостью
			изотропностью

№2 Сопротивление материалов – это наука о __________ элементов конструкций.

			прочности, жесткости и однородности
			прочности, жесткости и устойчивости
			жесткости, устойчивости и пластичности
			прочности, устойчивости и сплошности

№3 Если свойства материала в точке не зависят от направления, то такой материал называется …

			однородным
			анизотропным
			идеально упругим
			изотропным

№4 Напряжения и перемещения в сечениях, удаленных от места приложения внешней нагрузки, зависят от ее статического эквивалента и не зависят от способа ее приложения. Данное утверждение называется …

			принципом Сен-Венана
			гипотезой плоских сечений
			принципом начальных размеров
			принципом независимости действия сил

№5 Объемные силы имеют размерность …

№6 Напряжение − это сила, …

			приложенная к каждой единице площади поверхности тела
			приложенная к каждой единице объема тела
			приходящаяся на единицу площади сечения
			приложенная к точке поверхности тела

№7 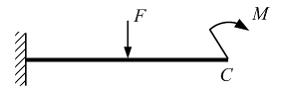Прогиб сечения С равен сумме прогибов, вызванных силой F и моментом М, приложенных по отдельности. Данное утверждение записано на основании принципа …

			Сен-Венана
			малых перемещений
			возможных перемещений
			независимости действия сил (принципа суперпозиции)

№8 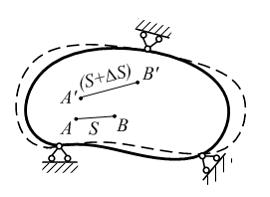В недеформированном теле расстояние между точками А и В равно S. В результате изменения формы и размеров тела точки А и В переместились в пространстве в положения  и . Расстояние между ними изменилось на величину . Линейной деформацией в точке А по направлению АВ называется величина …

№9 Свойство материала сохранять некоторую часть деформации после снятия нагрузки называется …

			жесткостью
			упругостью
			пластичностью
			твердостью

№10 Способность материала сопротивляться разрушению под действием внешних нагрузок называется …

			изотропностью
			твердостью
			упругостью
			прочностью

№11

Способность элементов конструкции сопротивляться внешним нагрузкам в отношении изменения формы и размеров называется …

			упругостью
			жесткостью
			устойчивостью
			твердостью

4. Модели прочностной надежности №1 В сопротивлении материалов все тела считаются …

			вязко-упругими
			абсолютно твердыми
			абсолютно упругими
			упруго-вязко-пластичными

№2 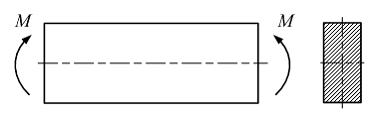Стержень изготовлен из пластичного материала c одинаковыми пределами текучести на растяжение и сжатие. Значения М и осевого момента сопротивления W заданы. Фактический коэффициент запаса прочности равен …

№3 Если свойства материала в точке не зависят от направления, то такой материал называется …

			идеально упругим
			анизотропным
			изотропным
			однородным

№4 Способность элементов конструкции сопротивляться внешним нагрузкам в отношении изменения формы и размеров называется …

			упругостью
			жесткостью
			устойчивостью
			твердостью

№5 Материал полностью заполняет объем тела и имеет беспустотную, бездефектную структуру. Данная гипотеза называется гипотезой …

			абсолютной упругости
			однородности
			изотропности
			сплошной среды

№6 Нагрузка, медленно растущая во времени, называется __________ нагрузкой.

			статической
			динамической
			ударной
			повторно-переменной

№7 В сопротивлении материалов основным методом расчета на прочность является метод расчета по …

			деформациям
			разрушающим нагрузкам
			предельным состояниям
			допускаемым напряжениям

№8 В сопротивлении материалов относительно структуры и свойств материала принимаются гипотезы …

			устойчивости, жесткости и прочности
			сплошности, однородности, изотропности и идеальной упругости
			сплошности, однородности и линейности
			изотропности, идеальной упругости и пластичности

№9 Расчетной схемой называется …

			математическая модель задачи
			объект, учитывающий влияние внешней нагрузки
			реальный объект, освобожденный от особенностей, несущественных при решении данной задачи
			абсолютно твердое тело

№10 Тело, один размер которого намного превышает два других, называется …

			массивом
			пластиной
			оболочкой
			стержнем