3. Ход работы

3.1 Вводим в программу cyst_mp порядок полиномов (=5) и исходные данные.

Полином А {1; 3; 5; 7; 9}.

Полином В {2; 4; 6; 8; 0}.

3.2 Изменение содержимого ячеек процессора на каждом такте работы:

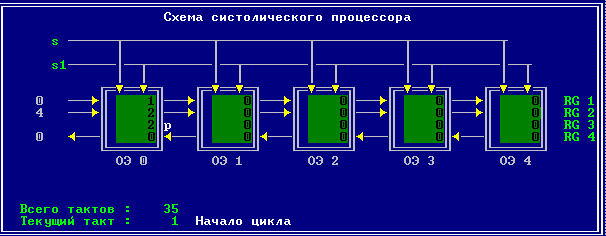
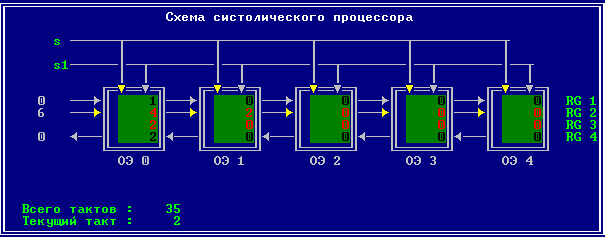
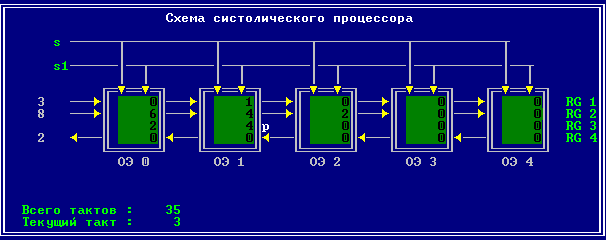
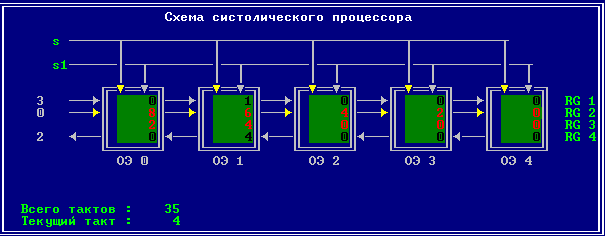
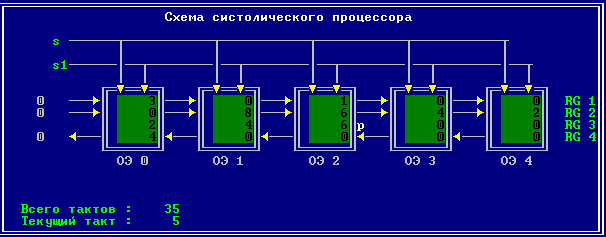
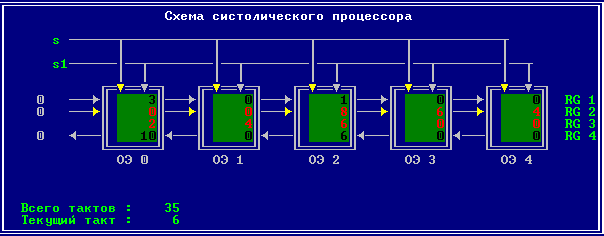
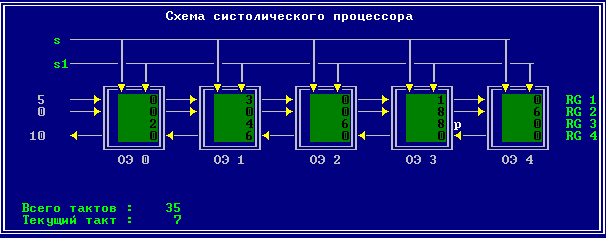
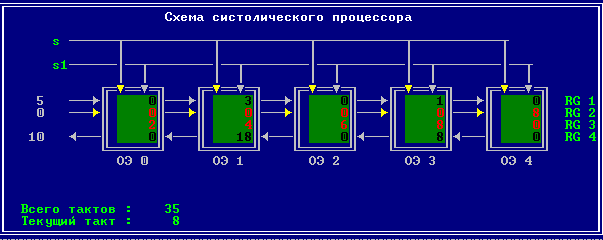
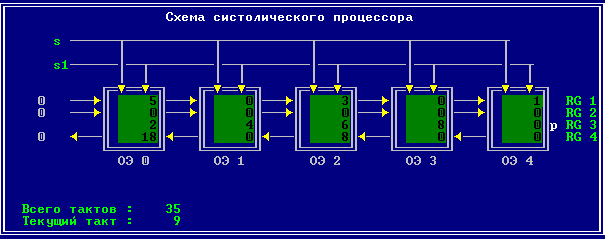
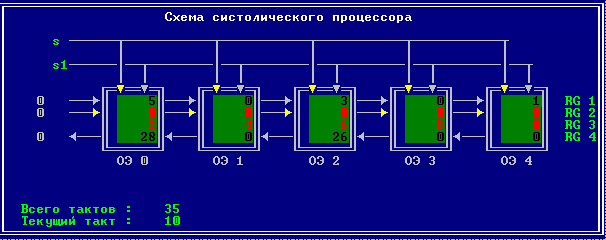
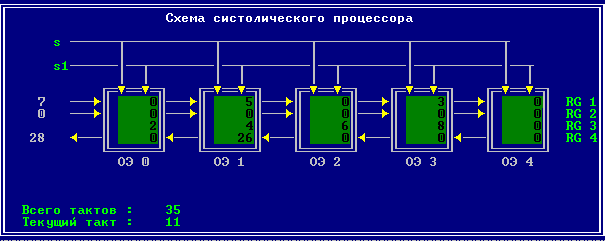
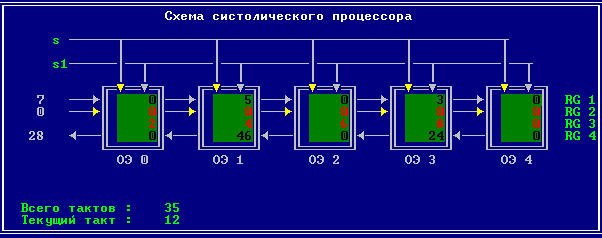
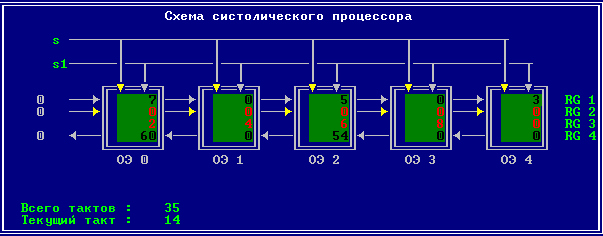
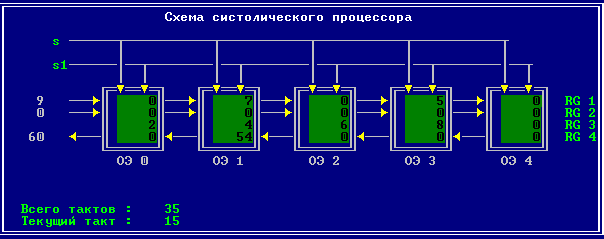
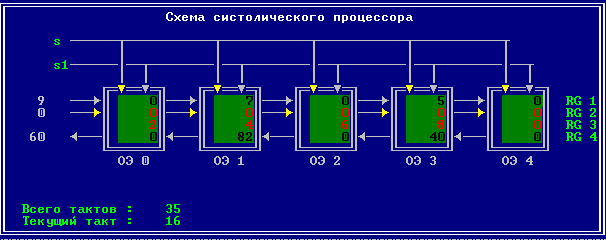
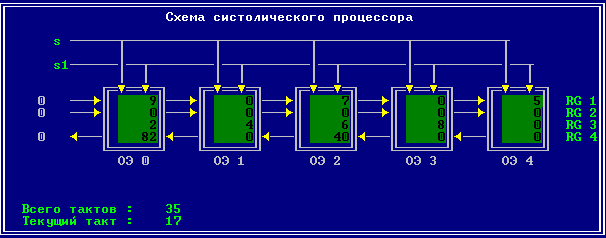
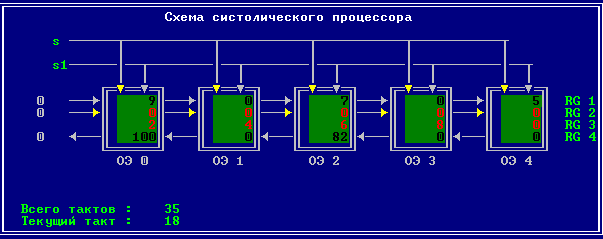
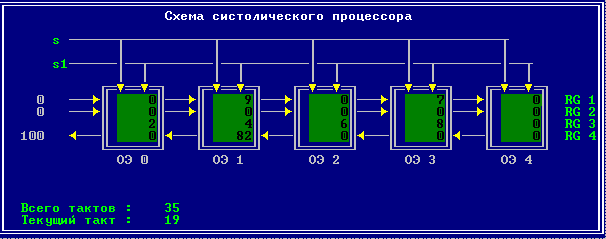
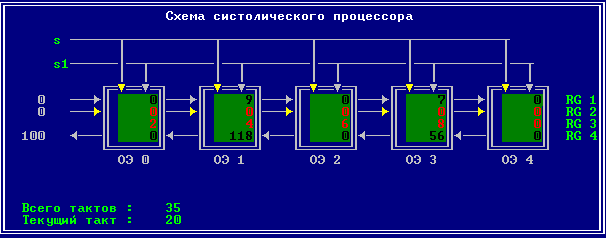
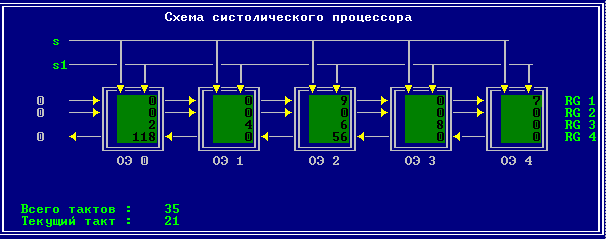
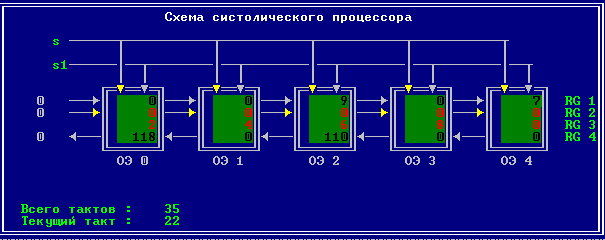
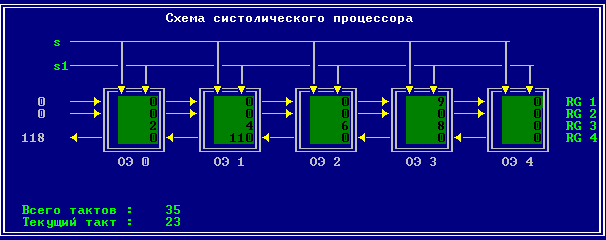
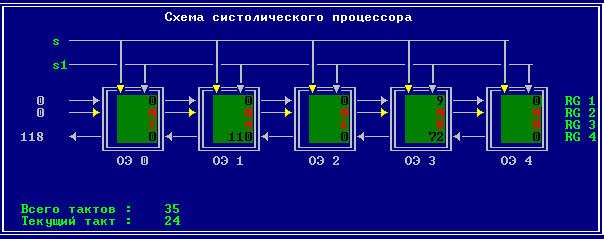
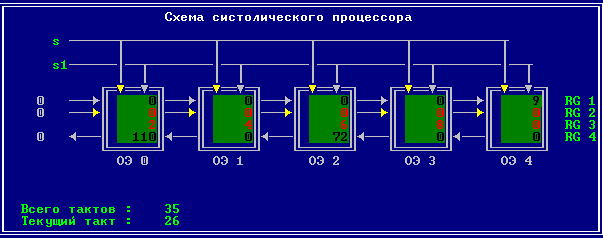
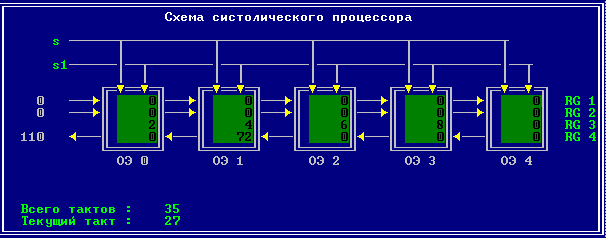
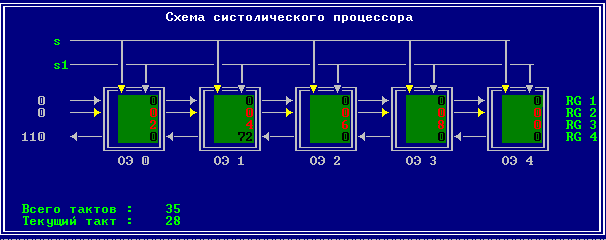
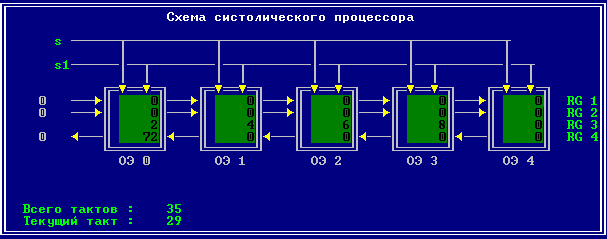
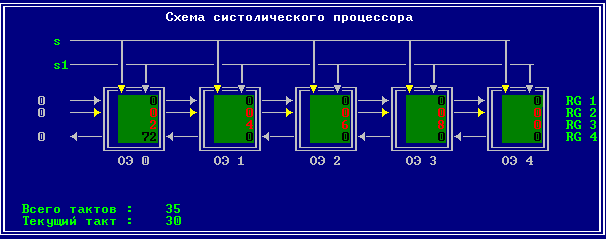
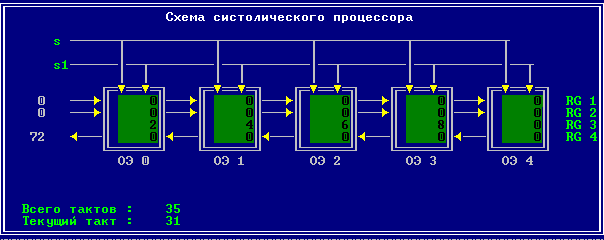
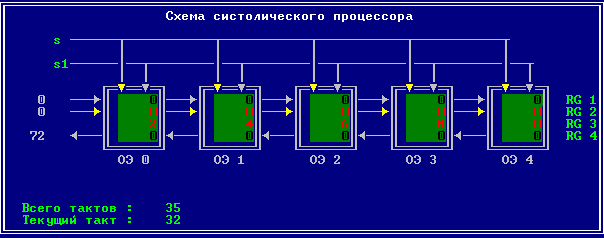
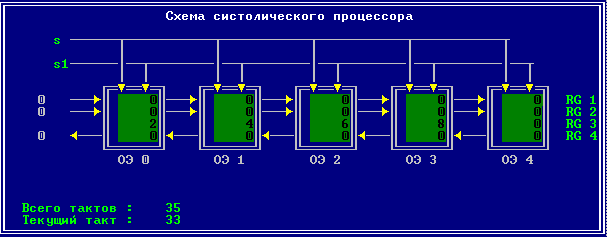
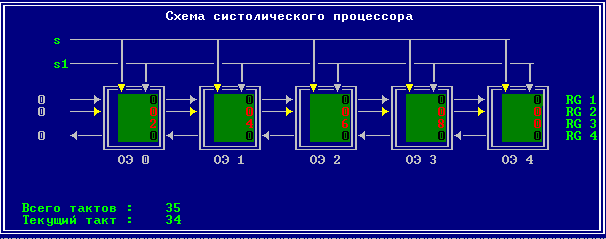
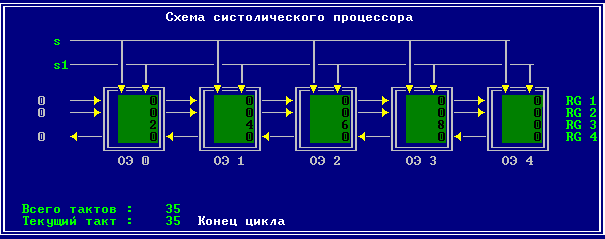
4. Аналитическое решение

Полином А: (1; 3; 5; 7; 9).

Полином В: (2; 4; 6; 8; 0).

4.1 Рассчитаем коэффициенты результирующего полинома:

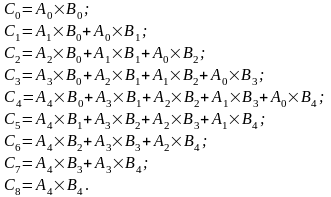
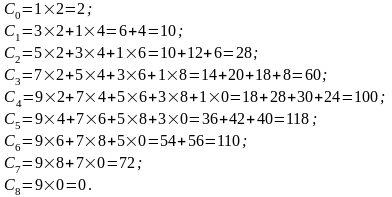
Результирующий полином: С= (2; 10; 28; 60; 100; 118; 110; 72; 0).

5. Вывод

В ходе выполнения лабораторной работы было выполнено умножение двух полиномов аналитическим методом и с использованием систолического процессора. В результате, задача перемножения полиномов 5-го порядка с использованием систолического процессора заняла 35 тактов. При аналитическом решении выполнили 41 операцию. Ускорение, полученное при использовании систолического процессора, составило:

.

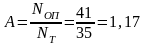II умножение матриц

1. Цель работы и задание:

1.1 Цель работы:

1 Изучить принцип работы систолического процессора для умножения матриц.

2 Провести экспериментальные исследования работы такого процессора.

1.2 Задание

Необходимо провести экспериментальные исследования работы систолического процессора для умножения матриц. Ввести свои наборы данных согласно выбранному варианту и получить результаты умножения. Необходимо вести запись содержимого процессора на каждом такте работы в пошаговом режиме. Вычислить конвейерный такт. Сделать вывод о работе систолического процессора, доказать повышение производительности по сравнению с обычным процессором.

Размерность матрицы А (4х6), размерность матрицы В (6х4).

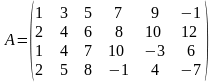
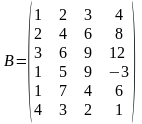
2. Теория

2.1 Краткая информация о работе ячейки

Необходимо быстро выполнить умножение двух матриц размером N x N A=[a_ij] и B=[b_ij] и найти третью матрицу C = A*B = [a_ij] * [b_ij] = [C_ij], элементы которой определяются как сумма произведений:

,

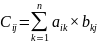где попарно умножаются k-е элементы j - го столбца B и i-й строки А. Рассмотрим пространственно-временную интерпретацию систолического алгоритма на простом примере при N=3. Элементы строк матрицы C вычисляются по формулам:

1) Первая строка:

C11 = a11b11 + a12b21 + a13b31,

C12 = a11b12 + a12b22 + a13b32,

C13 = a11b13 + a12b23 + a13b33.

2) Вторая строка:

C21 = a21b11 + a22b21 + a23b31,

C22 = a21b12 + a22b22 + a23b32,

C23 = a21b13 + a22b22 + a23b33.

3) Третья строка:

С31 = a31b11 + a32b21 + a33b31,

C32 = a31b12 + a32b22 + a33b32,

C33 = a31b13 + a32b23 + a33b33.

Каждая из строк С образуется по одинаковым формулам из одноименной строки А при поэлементном умножении на все столбцы В и сложении. Так как вычислительные алгоритмы в каждой из строк одинаковые, то их элементы можно образовать тремя одинаковыми векторными систолическими процессами, аналогичными предыдущему. Причем, потоки входных операндов по {a} у них будут разными соответственно первая, вторая и третья строки матрицы А, а потоки входных операндов по {b} одинаковые одни и те же элементы всех столбцов второй матрицы В.

В каждой ячейке ОЭ целесообразно выполнять одинаковые операции умножения и накапливающего сложения: c:= c + ab. Поэтому схемы ячеек ОЭ, схемы векторных систолических процессоров в каждой из строк и систолический алгоритм вычисления их элементов могут быть применены аналогичные предыдущему процессору. Необходимо лишь изменить способ ввода в ячейки ОЭ второй группы операндов - элементов {bij}.

При подборе этого нового способа их загрузки в процессор целесообразно исключать буферный регистр Рг3 и оставить в ячейке ОЭ только три регистра: Рг 1, Рг 2 для хранения соответственно элементов аij и bij и двойной регистр Рг 3 в накапливающем сумматоре (вместо Рг4).